Пример решенной контрольной работы по высшей математике
5.7 Исходя из определения непрерывности функции, выберите значение параметра а, при котором функция 1)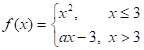
и 2) 
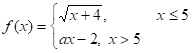
будет непрерывной, и нарисуйте ее график.
Решение:
1)
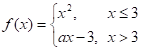
Функции 
и 
непрерывны в своих областях определения. Поэтому возможной точкой разрыва функции 
может быть точка 
.
По определению функция называется непрерывной если 
и запись для односторонних пределов: 
Поэтому для точки находим:
,
Исходя из определения непрерывности, функция будет непрерывной в точке если
, откуда параметр 
.
Изобразим график:
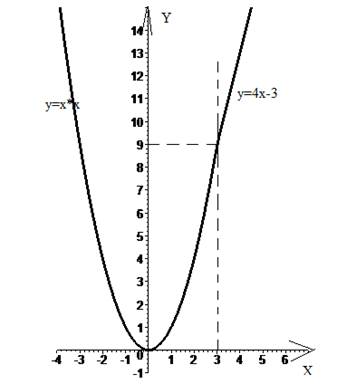
2)
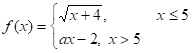
Функции 
и 
непрерывны в своих областях определения. Поэтому возможной точкой разрыва функции может быть точка 
.
По определению функция называется непрерывной если и запись для односторонних пределов:
Поэтому для точки находим:
,
Исходя из определения непрерывности, функция будет непрерывной в точке если
, откуда параметр 
.
Изобразим график:
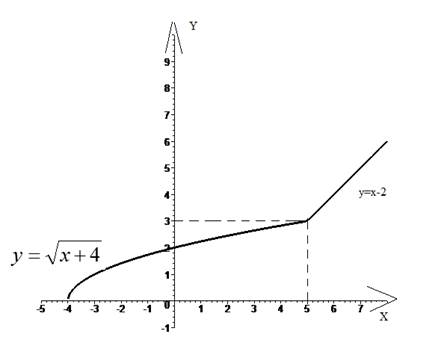
5.8 Используя свойства функций, непрерывных на отрезке, докажите, что уравнение 
имеет на отрезке [0;1] хотя бы один корень.
Решение:
Следствие 1 (первая теорема Больцано-Коши): Пусть функция непрерывна на отрезке 
. И пусть значения функций на концах отрезка имеют разные знаки: 
, 
или 
, 
. Тогда существует точка 
, значение функции в которой равно нулю.
Многочлен 
непрерывен на отрезке [0;1] так как он непрерывен в каждой точке этого отрезка. И так как 
и 
, то в силу следствия (первая теорема Больцано-Коши) существует точка 
, значение функции в которой равно нулю, т.е. 
. А это означает, что уравнение имеет корень на интервале 
.
6.1 (1-9) Найти производные следующих функций:
1)
2) 
3) 
4) 
5) 
6) 
7) 
8) 
9) 
Решение:
1)
Используем формулу для нахождения производной степенной функции: 
У нас 
2) 
Используем формулу для нахождения производной степенной функции:
У нас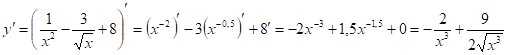 
3) 
Используем формулу для нахождения производной степенной функции:
У нас 
4)
Используем формулу для нахождения производной степенной функции: , а также как производную сложной функции:
5)
Используем формулу: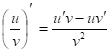 
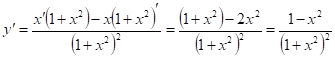
6)
Используем формулу: 
7)
Используем формулу:
8)
Используем формулу: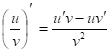
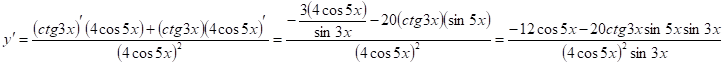
9)
Находим
6.3 Найдите дифференциал функции 
в точке 
при 
и вычислите приближенно 
Решение:
Вычислим дифференциал. Для начала найдем производную 
, а затем
. Тогда 
.
Вычислим теперь 
Ответ: 
6.4 Найдите дифференциал функции 
в точке 
при 
и вычислите приближенно 
Решение:
Вычислим дифференциал. Для начала найдем производную
, а затем
. Тогда 
.
Вычислим теперь 
Ответ: 
6.5(1) Найдите дифференциал функции 
в точке 
при произвольном 
Решение:
Так как дифференциал функции 
, то находим производную:
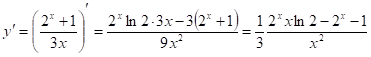
Тогда 
Ответ: 
6.6 Напишите уравнения касательной и нормали к графику функции 
в точке с абсциссой 
:
1) 
2) 
3) 
Решение:
Уравнение касательной: 
Уравнение нормали 
.
1)
Находим
, 
,
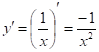Тогда уравнение касательной примет вид: 
, т.е. 
Уравнение нормали 
, т.е. 
2) 
Находим
, 
,
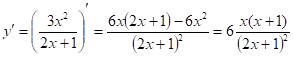Тогда уравнение касательной примет вид: 
, т.е. 
Уравнение нормали 
, т.е. 
3) 
Находим
, 
,
Тогда уравнение касательной примет вид: 
, т.е. 
Уравнение нормали 
, т.е. 
Ответ: 1) - уравнение касательной, 
- уравнение нормали
2) - уравнение касательной, - уравнение нормали
3) - уравнение касательной, - уравнение нормали
6.8 Напишите уравнения касательной к графику функции 
в точке пересечения этого графика с прямой 
.
Решение:
Найдем точки пересечения графика функции
с прямой 
из уравнения:
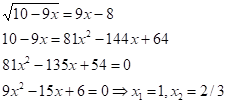
- не является корнем.
- является корнем. Поэтому находим
Тогда уравнение касательной в точке примет вид: 
, т.е. 
Ответ: 