Примеры решения задачи по строительной механике(линии влияния составной балки)
Ниже приведены условие и решение задачи. Закачка решения в формате pdf начнется автоматически через 10 секунд.
1
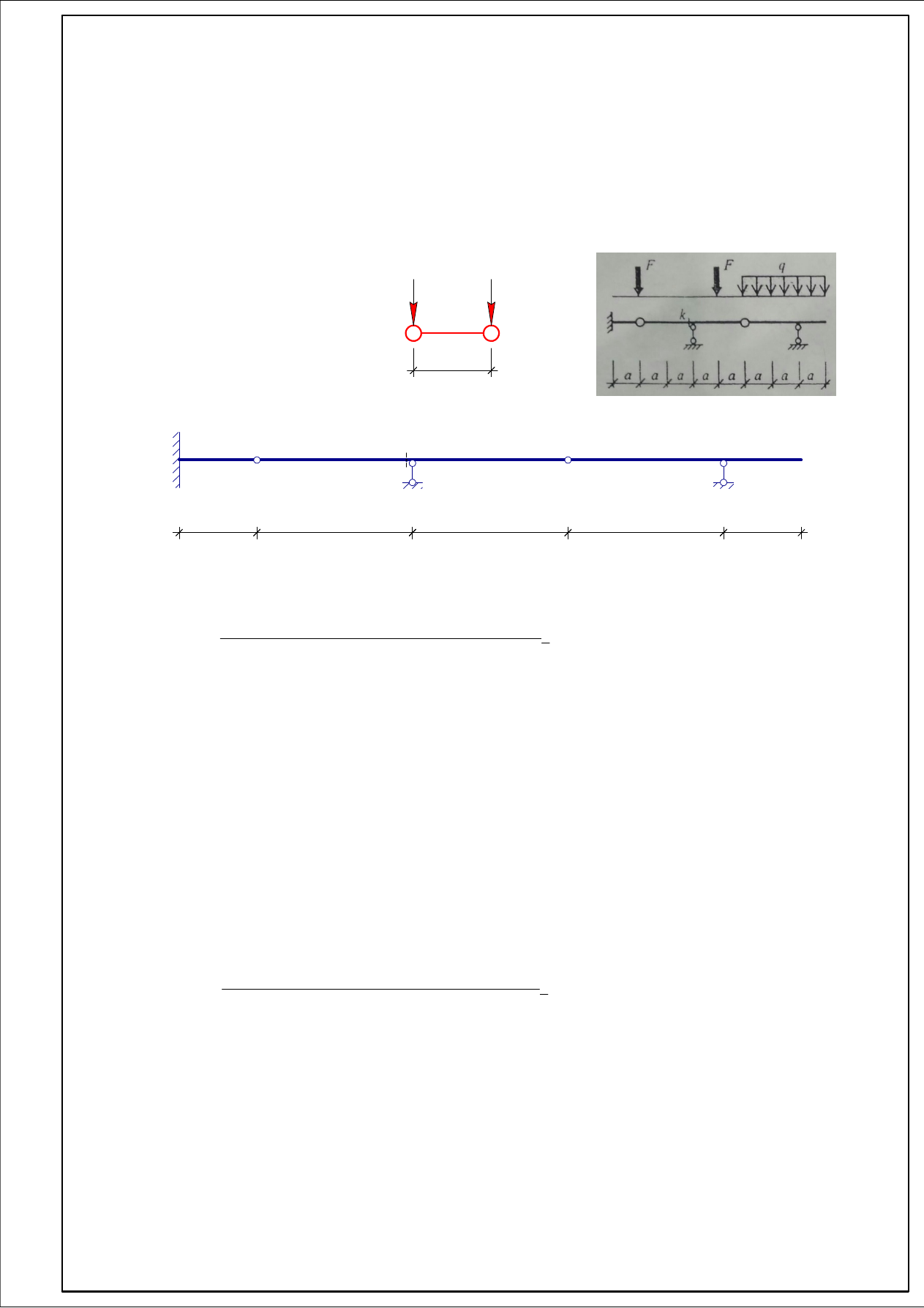
Для заданной многопролётной статически определимой балки требуется:
1. Построить линии влияния для всех опор и линии влияния Q и M для сечения K;
2. Загрузить все линии влияния заданной нагрузкой;
3. Загрузить все линии влияния наиболее опасным образом временной нагрузкой в
виде распределенной нагрузки q
вр
= 15 кН/м (рассмотреть два худших случая -
минимальное значение и максимальное значение);
4. Загрузить все линии влияния наиболее опасным образом подвижной нагрузкой в
виде двухосной тележки с давлением Q = 20 кН на каждую ось (расстояние между осями
1,5 м).
Исходные данные:
a = 3 м;
1.
Построим линии влияния для всех опор и линии влияния Q и M для сечения K.
Построим линию влияния опорного момента M
A
. Линия влияния опорного момента -
это график зависимости опорного момента от подвижной единичной силы P = 1.
Рассмотрим балку AB:
При действии единичной силы над балкой, момент составит:
M
A
= -1·x;
При действии единичной силы в защемлении момент будет нулевым, при действии
единичной силы в шарнире момент будет равен "-3". Через найденные значения
проведём прямую.
При нахождении единичной силы над балкой BD (между сечениями B и C) нагрузка
на правый край балки будет меняться от 1 до нуля (нулевым значением будет когда
единичная сила будет находиться над опорой C), значение опорного момента M будет
меняться от "-3" до нуля. Через найденные значения проведём прямую и удлиним её до
краев балки.
При нахождении единичной силы над остальными опорами, M
A
будет равен нулю.
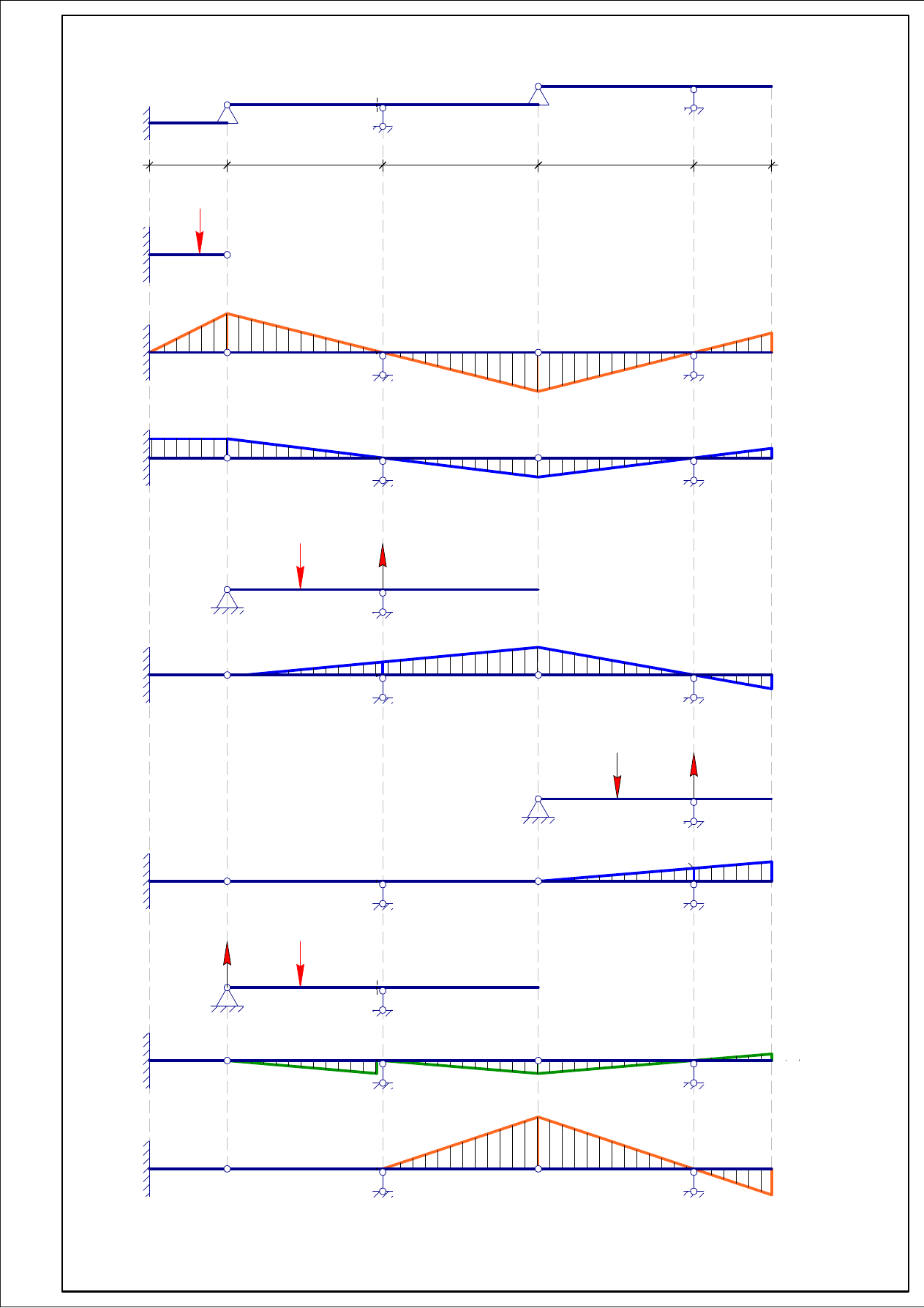
Изобразим полученную линию влияния.
Построим линию влияния опорной реакции V
A
. Линия влияния опорной реакции -
это график зависимости опорной реакции от подвижной единичной силы P = 1.
Рассмотрим балку AB:
При действии единичной силы в защемлении и на протяжении всей балки, опорная
реакция будет равна единице. При нахождении единичной силы над балкой BD (между
сечениями B и C) нагрузка на правый край балки будет меняться от "1" до нуля
(нулевым значением будет когда единичная сила будет находиться над опорой C). Через
найденные значения проведём прямую и удлиним её до краев балки;
При нахождении единичной силы над остальными опорами, реакция V
A
будет равна
нулю.
Изобразим полученную линию влияния.
1
A
3
6
D
6
6
3
C
B
E
K
3
6
6
6
3
1 ,5
20 кН
20 кН
1 ,5
2
2
A
3
6
6
6
3
A
B
C
D
E
K
Поэтажная
схема
Л.в. Q
K
Л.в. V
C
2
1
Л.в. V
E
1
Л.в. M
K
Л.в. M
A
3
-3
-1,5
Л.в. V
A
1
0,5
-1
-1
1,5
0,5
-1
-1
3
-6
V
E
1
E
D
B
1
V
C
C
D
1
A
B
B
1
C
D
V
B
K
3
6
6
6
3
V
E
V
C
V
B

Построим линию влияния опорной реакции V
C
.
Рассмотрим балку BD:
При действии единичной силы над опорой C, опорная реакция будет равна единице.
При нахождении единичной силы над шарниром B, опорная реакция V
C
будет равна
нулю. Через найденные значения проведём прямую и удлиним её до краев балки;
Из подобия треугольников найдём значение опорной реакции при действии
единичной нагрузки на правом краю балки:
x
1
=
12
6
=> x =
12
6
= 2;
При нахождении единичной силы над остальными опорами, реакция V
C
будет равна
нулю.
При нахождении единичной силы левее шарнира B нагрузка на рассматриваемую
балку передаваться не будет.
Изобразим полученную линию влияния.
Построим линию влияния опорной реакции V
E
.
Рассмотрим балку DE:
При действии единичной силы над опорой E, опорная реакция будет равна единице.
При нахождении единичной силы над шарниром D, опорная реакция V
E
будет равна
нулю. Через найденные значения проведём прямую и удлиним её до краев балки;
При нахождении единичной силы левее шарнира D нагрузка на рассматриваемую
балку передаваться не будет.
Изобразим полученную линию влияния.
Построим линию влияния Q для сечения K.
Линия влияния поперечной силы для сечения K - график зависимости поперечной
силы в данном сечении от подвижной единичной силы P = 1.
Рассмотрим балку BD:
При нахождении единичной силы левее рассматриваемого сечения усилие в
шарнире V
B
будет:
∑
M
C
= 0:
- 1·x + V
B
·6 = 0;
V
B
=
x
6
=> Q = V
B
- 1 =
x
6
- 1;
При нахождении единичной силы в шарнире B (x = 6), Q =
6
6
- 1 = 0;
- над опорой C (x = 0), Q = 0 - 1 = -1;
При нахождении единичной силы правее опоры C усилие в шарнире V
B
будет:
∑
M
C
= 0:
1·x + V
B
·6 = 0;
V
B
= -
x
6
=> Q = - V
B
= -
x
6
;
При нахождении единичной силы в шарнире D (x = 6), Q = -
6
6
= -1;
- над опорой C (x = 0), Q = 0;
При действии единичной силы над опорами, расположенными правее, поперечная
сила будет нулевой.
При нахождении единичной силы левее шарнира B, нагрузка на рассматриваемую
балку передаваться не будет.
Изобразим полученную линию влияния.
3
3

4
Построим линию влияния изгибающего момента для сечения K.
Линия влияния изгибающего момента для сечения K - график зависимости
изгибающего момента в данном сечении от подвижной единичной силы P = 1.
Рассмотрим балку BD:
При нахождении единичной силы левее рассматриваемого сечения, усилие в
шарнире V
B
будет:
∑
M
C
= 0:
- 1·x + V
B
·6 = 0;
V
B
=
x
6
;
Изгибающий момент в сечении K будет находиться как:
M
K
= - 1·x + V
B
·6 = - 1·x +
x
6
·6 = 0;
При нахождении единичной силы правее рассматриваемого сечения, усилие в
шарнире V
B
будет:
∑
M
C
= 0:
1·x + V
B
·6 = 0;
V
B
= -
x
6
;
Изгибающий момент в сечении K:
M
K
= V
B
·6 = -
x
6
·6 = - x;
При нахождении единичной силы в шарнире D (x = 6), M
K
= -6;
- над опорой C (x = 0), M
K
= 0;
При
действии
единичной
силы
над
опорами,
расположенными
правее
рассматриваемой балки, момент M
K
будет нулевым.
При нахождении единичной силы левее шарнира B, нагрузка на рассматриваемую
балку передаваться не будет.
Изобразим полученную линию влияния.
2.
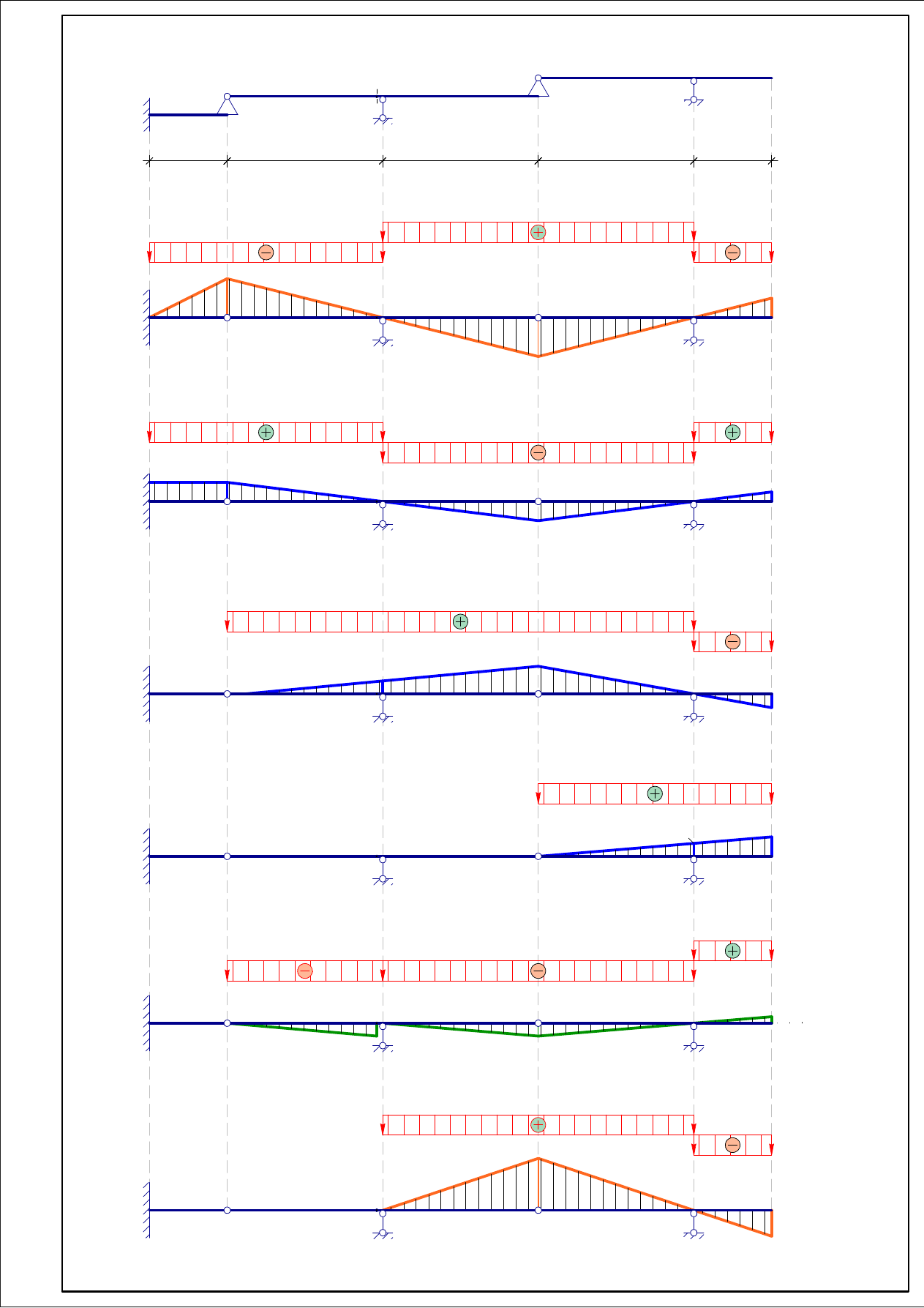
Загрузим все линии влияния заданной нагрузкой.
Для определения усилий R, Q и M по линиям влияния, используем формулу:
R =
∑
n
i= 1
P
i
·y
i
+
∑
n
i= 1
q
i
·ω
i
+
∑
n
i= 1
m
i
·tg(α
i
),
где P
i
– сосредоточенная сила, действующая на сооружение;
y
i
– ордината линии влияния под сосредоточенной силой P
i
;
q
i
– интенсивность распределенной нагрузки;
ω
i
– площадь части линии влияния R, которая находится под участком действия
равномерно распределенной нагрузки интенсивности q
i
;
m
i
– сосредоточенный момент;
tg(α
i
) – тангенс угла наклона той части линии влияния к оси балки (базовой прямой), где
приложен момент m
i
;
Нагрузка (P
i
, q
i
) направленная сверху вниз, считается положительной, а снизу вверх
– отрицательной.
Знаки для y
i
и ω
i
принимаются согласно знакам, поставленным на самой линии
влияния реакции R;
Произведение m
i
·tg(α
i
) можно считать положительным, если направляющий вектор
сосредоточенного момента М пытается «прижать» л.в. к базовой линии.
M
A
= 40·(-3) + 40·1,5 + 30·[
1
2
·3·6 +
1
2
·(-1,5)·3 ] =
142,5 кН·м
;
V
A
= 40·1 + 40·(-0,5) + 30·[
1
2
·(-1)·6 +
1
2
·0,5·3 ] =
-47,5 кН
;
V
C
= 40·1,5 + 30·[
1
2
·2·6 +
1
2
·(-1)·3 ] =
195 кН
;
V
E
= 30·(
1
2
·1,5·9) =
202,5 кН
;
Q
K
= 40·(-0,5) + 30·[
1
2
·(-1)·6 +
1
2
·0,5·3 ] =
-87,5 кН
;
M
K
= 40·(-3) + 30·[
1
2
·(-6)·6 +
1
2
·3·3 ] =
-525 кН·м
.
4
5
5
3
6
6
6
3
A
B
C
D
E
K
Л.в. Q
K
Л.в. V
C
2
1
Л.в. V
E
1
Л.в. M
K
Л.в. M
A
3
-3
-1,5
Л.в. V
A
1
0,5
-1
-1
1,5
0,5
-1
-1
3
-6
Поэтажная
схема
3
6
6
6
3

6
3.
Загрузим все линии влияния наиболее опасным образом временной нагрузкой в
виде распределенной нагрузки.
M
MAX
A
= q
вр
·(
1
2
·3·12·
1,25
2
) = 15·18 =
270 кН·м
;
M
min
A
= q
вр
·[
1
2
·(-3)·9 +
1
2
·(-1,5)·3 ] = -15·15,75 =
-236,25 кН·м
;
V
MAX
A
= q
вр
·[1·3 +
1
2
·1·6 +
1
2
·0,5·3 ] = 15·6,75 =
101,25 кН
;
V
min
A
= q
вр
·[
1
2
·(-1)·12 ] = -15·6 =
-90 кН
;
V
MAX
C
= q
вр
·[
1
2
·2·18 ] = 15·18 =
270 кН
;
V
min
C
= q
вр
·[
1
2
·(-1)·3 ] = -15·1,5 =
-22,5 кН
;
V
MAX
E
= q
вр
·[
1
2
·1,5·9 ] = 15·6,75 =
101,25 кН
;
V
min
E
=
0
;
Q
MAX
K
= q
вр
·[
1
2
·0,5·3 ] = 15·0,75 =
11,25 кН
;
Q
min
K
= q
вр
·[
1
2
·(-1)·6 +
1
2
·(-1)·12 ] = -15·9 =
-135 кН
;
M
MAX
K
= q
вр
·[
1
2
·3·3 ] = 15·4,5 =
67,5 кН·м
;
M
min
K
= q
вр
·[
1
2
·(-6)·12 ] = -15·36 =
-540 кН·м
.
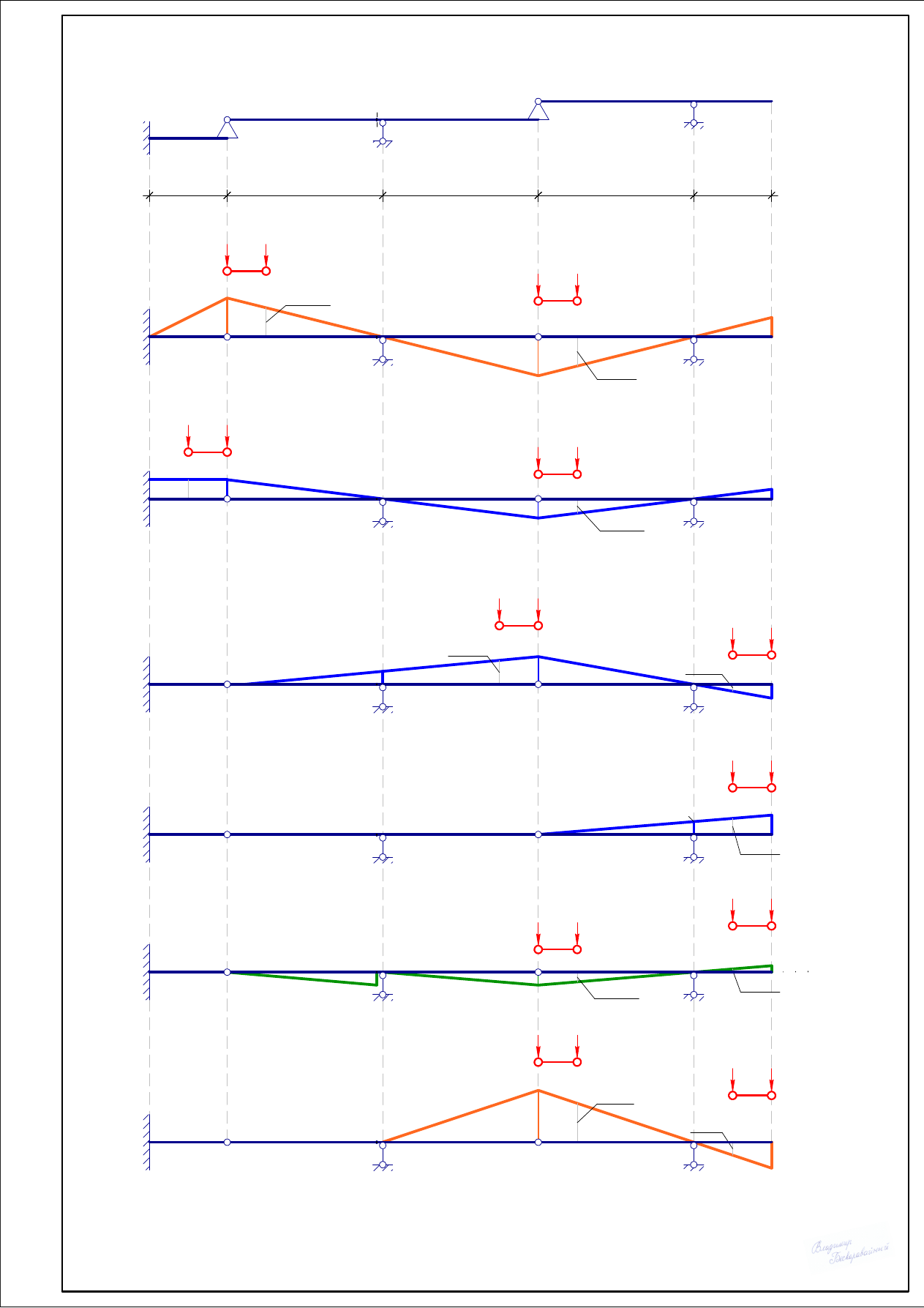
4.
Загрузим все линии влияния наиболее опасным образом подвижной нагрузкой в
виде двухосной тележки.
M
MAX
A
= 20·3 + 20·2,25 =
105 кН·м
;
M
min
A
= 20·(-3) + 20·(-2,25) =
-105 кН·м
;
V
MAX
A
= 20·1 + 20·1 =
40 кН
;
V
min
A
= 20·(-1) + 20·(-0,75) =
-35 кН
;
V
MAX
C
= 20·2 + 20·1,75 =
75 кН
;
V
min
C
= 20·(-1) + 20·(-0,5) =
-30 кН
;
V
MAX
E
= 20·1,5 + 20·1,25 =
55 кН
;
V
min
E
=
0 кН
;
Q
MAX
K
= 20·0,5 + 20·0,25 =
15 кН
;
Q
min
K
= 20·(-1) + 20·(-0,75) =
-35 кН
;
M
MAX
K
= 20·3 + 20·1,5 =
90 кН·м
;
M
min
K
= 20·(-6) + 20·(-4,5) =
-210 кН·м
.
S
непод
S
M AX
вр
S
m in
вр
S
M A X
непод
S
m in
непод
S
M AX
р асч
S
m in
р асч
M
A
142,5
270
-236,25
105
-105
517,5
-198,75
V
A
-47,5
101,25
-90
40
-35
93,75
-172,5
V
C
195
270
-22,5
75
-30
540
142,5
V
E
202,5
101,25
0
55
0
358,75
202,5
Q
K
-87,5
11,25
-135
15
-35
-61,25
-257,5
M
K
-525
67,5
-540
90
-210
-367,5
-1275
6
7
7
3
6
6
6
3
Поэтажная
схема
Л.в. Q
K
Л.в. V
C
2
1
Л.в. V
E
1
Л.в. M
K
Л.в. M
A
3
-3
-1,5
Л.в. V
A
1
0,5
-1
-1
1,5
0,5
-1
-1
3
-6
-2 ,2 5
2 ,2 5
-0 ,7 5
-0 ,5
1 ,7 5
1 ,2 5
0 ,2 5
-0 ,7 5
-4 ,5
1 ,5
20 кН
20 кН
20 кН
20 кН
20 кН
20 кН
20 кН
20 кН
20 кН
20 кН
20 кН
20 кН
20 кН
20 кН
20 кН
20 кН
20 кН
20 кН
20 кН
20 кН
20 кН
20 кН
A
B
C
D
E
K
3
6
6
6
3
Имя файла: raschyot_mnogoproletnoj_balki.pdf
Размер файла: 203.75 Kb
Если закачивание файла не начнется через 10 сек, кликните по этой ссылке
