Примеры решения задачи по строительной механике(расчет составной балки)

    Для балки требуется :

    1. Используя индивидуальный шифр выбрать : расчётную схему балки, её размеры, действующую нагрузку.

    2. Провести кинематический анализ балки, построив её этажную схему.

    3. Рассчитать отдельные простые балки и построить для них эпюры М и Q.

    4. Построить эпюры усилий для исходной составной балки.

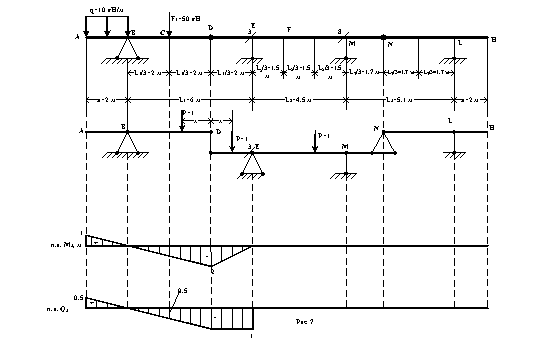
    5. Построить линии влияния : двух опорных реакций (по собственному выбору), двух изгибающих моментов Mi, Mk и двух поперечных сил Qi, Qk (номера точек i, k даются в таблице).

    6. Загрузить одну из линий влияния (по выбору) заданной нагрузкой, определить по ней соответствующие усилие и сравнить его со значением, полученным в п. 3.

    Дано :

№ схемы	№ загружения	L1 ,    м	L2 ,    м	L3,     м	а,     м	F1,    кН	F2,    кН	q,  кН/м	i	k
3	0	6	4.5	5.1	2	50	28	10	3	8

                                                                 Решение.

    1. Составляем расчётную схему балки.

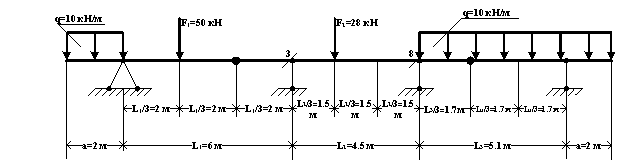
    2. Кинематический анализ схемы, построение её этажной схемы.

    Степень свободы балки по формуле :

                                W=3Д-2Ш-С0

    где Д – число дисков ; Ш – число простых шарниров ; C0 – число опорных связей.

    В нашем случае : Д=3 ; Ш=2 ; C0=5.

    Тогда степень свободы балки :

                                 W=3×3-2×2-5=9-4-5=0

    На рисунке 1 построена поэтажная схема. Составная балка состоит из трёх дисков : DN – основная балка, к которой присоединены второстепенные – AD и NH.

    Таким образом, балка не подвижна, геометрически неизменяема и статически определима.

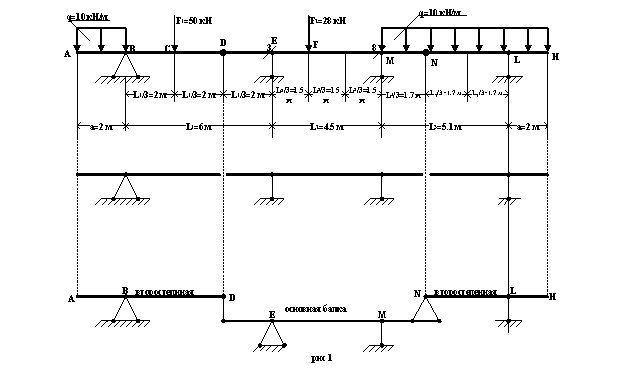
    3. Рассчитаем отдельные простые балки и построим эпюры М и Q.

    Балка NH. Определим опорные реакции :

             ΣmL=0  ;  -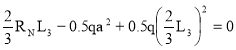 

             RN= кН

             ΣmN=0  ;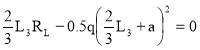 

             RL= кН

    Контроль :

             ΣY=RL+RN-q(2L3/3+a)=11.12+42.88-10×(3.4+2)=0

    Запишем выражения Q и М для каждого участка.

    Участок NL : 0<x1<3.4 м (ход слева)

     Q1=RN-qx1  ;   M1=RNx1-0.5qx12

    Участок LH : 0<x2<2 м (ход справа)

     Q2=qx2  ;  M2=-0.5qx22

    Находим значения Q и М в характерных точках балки.

    Участок NL : при x1=0

       QN=RN=11.12 кН  ;  MN=0

                            при x1=3.4 м

       QLл=RN-3.4q=11.12-3.4×10=-22.88 кН  ; 

       MLл=3.4RN-0.5q·3.42=3.4×11.12-0.5×10×3.42= -20 кН·м

    На участке NL эпюра М ограничена параболой, имеющей экстремум. Найдём абсциссу сечения, где момент имеет экстремум из условия Q1=RN-qx0=0 ; x0=RN/q=11.12/10=1.1 м.

    Значение экстремального момента :

             Mэкс=RNx0-0.5qx02=11.12×1.1-0.5×10×1.12=6.2 кН·м

    Участок LH : при x2=2 м

        QLпр=2q=2×10=20 кН  ;  MLпр=-0.5q·22=-0.5×10×22=-20 кН·м

                            при x2=0

      QH=0  ;  MH=0

    На основании вычислений эпюры Q и М построены на рисунке 2.  

    Балка AD. Определим опорные реакции.

           ΣmD=0  ; 

                            RB=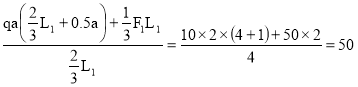 кН

         ΣmB=0  ; 

                            RD=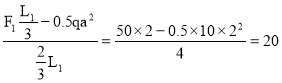 кН

    Контроль :

          ΣY=RB+RD-F1-qa=50+20-50-10×2=0

    Запишем выражения Q и М для каждого участка.

    Участок AB : 0<x1<2 (ход слева).

           Q1= -qx1  ;  M1=-0.5qx12

    Участок BC : 2<x2<4 (ход лева).

           Q2=-qa+RB  ;  M2=-qa(x2-0.5a)+RB(x2-a)

    Участок CD : 0<x3<2 (ход справа).

           Q3=-RD  ;  M3=RDx3

    Находим Q и М в характерных точках балки.

    Участок AB : при x1=0

            QA=0  ;  MA=0

                            при x1=2 м

             QBл=-2q=-2×10= -20 кН ; MBл=-0.5q·22=-0.5×10×4= -20 кН·м

    Участок BC : при x2=2

             QBпр=-qa+RB=-10×2+50=30 кН ;

             MBпр=-qa(2-0.5a)+RB(2-a)=-10×2×1=-20 кН·м

                            при x2=4

             QCл=-qa+RB=-10×2+50=30 кН ;

             MCл=-qa(4-0.5a)+RB(4-a)=-10×2×(4-1)+50×(4-2)=40 кН·м

    Участок CD : при x3=2

             QCпр=-RD=-20 кН  ;  MCпр=2RD=2×20=40 кН·м

                            при x3=0

             QD=-RD=-20 кН  ;  MD=0

    Эпюры Q и М построены на рисунке 2.

    Балка DN. Определим опорные реакции.

               ΣmM=0  ;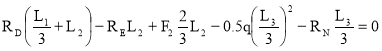              

      RE=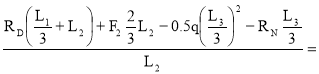

             кН

               ΣmE=0  ; 

    RM=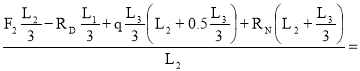

          кН

    Контроль :

       ΣY=-RD+RE-F2+RM-1.7q-RN= -20+40.14-28+35.98-1.7×10-11.12=0

    Запишем выражения Q и М для каждого участка.

    Участок DE : 0<x1<2 (ход слева)

         Q1= -RD  ;  M1=-RDx1

    Участок EF : 2<x2<3.5 (ход слева)

         Q2=-RD+RE  ;  M2=-RDx2+RE(x2-L1/3)

    Участок FM : 1.7<x3<4.7 (ход справа)

         Q3=qL3/3+RN-RM  ;  M3=-RNx3-q(L3/3)(x3-0.5L3/3)+RM(x3-L3/3)

    Участок MN : 0<x4<1.7

          Q4=qx4+RN  ;  M4=-0.5qx42-RNx4

    Находим Q и М в характерных точках балки.

    Участок DE : при x1=0

                   QD=-RD=-20 кН  ;  MD=0

                           при x1=2 м

                   QEл=-RD=-20 кН  ;  MEл=-2RD=-2×20=-40 кН·м

    Участок EF : при x2=2 м

                    QEпр=-RD+RE=-20+40.14=20.14 кН ;

                    MEпр=-2RD+RE(2-2)=-2×20=-40 кН

                           при x2=3.5 м

                    QFл=-RD+RE=-20+40.14=20.14 кН

                    MFл=-3.5RD+RE(3.5-2)=-3.5×20+40.14×1.5=-9.79 кН·м

    Участок FM : при x3=4.7 м

                     QFпр=qL3/3+RN-RM=10×1.7+11.12-35.98= -7.86 кН

                     MFпр=-4.7RN-q(L3/3)(4.7-0.5L3/3)+RM(4.7-L3/3)=

                             =-4.7×11.12-1.7×10×(4.7-0.5×1.7)+35.98×(4.7-1.7)= -9.77 кН·м

                            при x3=1.7 м

                      QMл=qL3/3+RN-RM=10×1.7+11.12-35.98=-7.86 кН

                      MMл=-1.7RN-q(L3/3)(1.7-0.5L3/3)+RM(1.7-L3/3)=

                             =-1.7×11.12-10×1.7×(1.7-0.5×1.7)= -33.35 кН·м

    Участок MN : при x4=1.7

                       QMпр=1.7q+RN=1.7×10+11.12=28.12 кН

                        MMпр=-0.5q·1.72-1.7RN=-0.5×10×1.72-1.7×11.12=-33.35 кН·м

                             при x4=0

                        QN=RN=11.12 кН

                        MN=0

    Эпюры Q и М построены на рисунке 2.

 

 

 

 

 

 

 

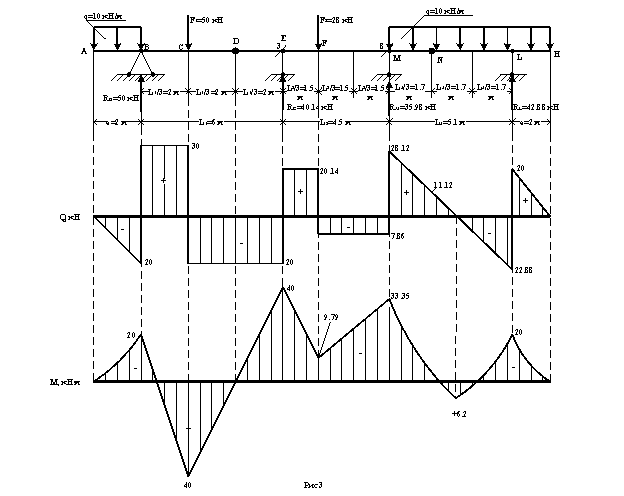
    4. Эпюры Q и М для исходной составной балки.

    Объединяя эпюры Q и М, построенные для каждой простой балки в одну, получим эпюры Q и М для исходной составной балки.

    Эпюры Q и М для составной балки построены на рисунке 3.

    5. Построение линий влияния.

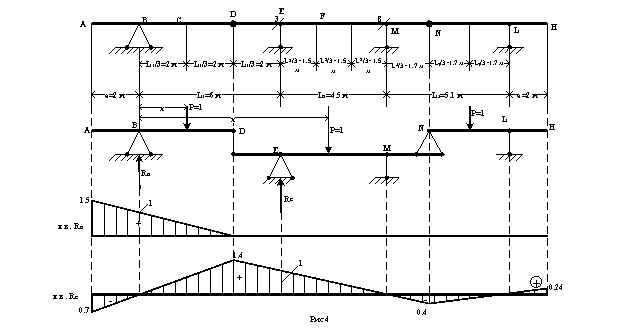
    Построение линии влияния реакции RB.

    Располагаем начало координат в точке B. Пусть сила P=1 движется по балке AD. Тогда уравнение равновесия балки :

                   ΣMD=0 ; -4RB+P(4-x)=0

    Отсюда уравнение линии влияния RB  на участке AD имеет вид :

                   RB==1-x/4

    Строим линию влияния RB по двум точкам :

                   при x=0 (сила P располагается в точке B) – RB=1

                   при x=4 (сила P располагается в точке D) – RB=0

    Найдём ординату линии влияния в точке А :

                    при x=-2 (сила P располагается в точке А) – RB=1.5

    При движении силы P=1 по участкам DN и NH RB=0, так как при положениях груза P=1 на этих участках балка AD не работает. Линия влияния RB построена на рисунке 4.

    Построение линии влияния RE.

    При расположении силы P=1 на участке DN уравнение линии влияния RE найдём из уравнения равновесия балки :

                    ΣMM=0  ;  -4.5RE+P(10.5-x)=0

                                       RE=  

    Эту линию строим по двум точкам :

                     при x=6 (сила P располагается в точке Е) – RE=1 ;

                     при x=10.5 (сила P располагается в точке М) – RE=0

    Определим ординаты линии влияния RE в точках D и N :

                    при x=4 (сила P находится в точке D) – RE=1.4

                    при x=12.2 (сила P находится в точке N) – RE=-0.4

    Линию влияния RE на участке AD строим по двум точкам. В точке D ордината линии влияния участка AD совпадает с ординатой линии влияния участка DN. В точке B – RE=0. Через эти точки проводим линию влияния RE на участке AD.

   Определим ординату линии влияния в точке А.

               RE=1.4RD, где RD – реакция в точке D. Определим её из уравнения равновесия балки AD :

                         4RD-Px=0  ;  RD=x/4

    Тогда уравнение линии влияния на участке AD имеет вид :

                         RE= ; при x=-2 (сила P располагается в точке А) – RE=-0.7

    Аналогично строим линию влияния на участке NH. В точке N – RE=-0.4 ; в точке L – RE=0. Найдём ординату линии влияния в точке H.

                RE=-0.4RN , где RN – реакция в точке N. Определим её из уравнения равновесия балки NH :

                      -3.4RN+P(15.6-x)=0  ;  RN=  - уравнение линии влияния на участке NH.

                       при x=17.6 (сила P располагается в точке H) – RE= 

    Линия влияния RE построена на рисунке 4.

    Построение линии влияния изгибающего момента в сечении 3 (левее точки Е, бесконечно близко к ней).

    При движении P=1 по участку DE левее точки 3, рассматривая равновесие левой отсечённой части (относительно точки 3) балки DN, имеем :

                      M3=-P(2-x)=-(2-x)

    при x=0 (точка D) – M3=-2 м ; при x=2 м (точка Е) – M3=0.

    По этим точкам строим линию влияния М3 на участке DE.

    При движении P=1 по участку ED правее точки 3, рассматривая равновесие левой отсечённой части балки DN, имеем :

                      M3=0

    При движении P=1 по участку EN балки DN и по балки NH, рассматривая равновесие левой отсечённой части балки DN, также получим : M3=0. Т.е. на участках EN и NH линия влияния совпадает с осью абсцисс.

    При движении P=1 по балке AD М3=-2RD, где RD находим из уравнения равновесия балки AD :

                    ΣmB=0 ; -P(-4-x)-4RD=0  ;  RD= 

    Тогда уравнение линии влияния М3=

    при x=0 (точка D) – M3=-2 м ; при x=-4 м (точка B) – M3=0 ; при x=-6 м (точка А) – М3=1 м.

    Линия влияния М3 построена на рисунке 5.

    Построение линии влияния поперечной силы Q3 в сечении 3 (левее точки Е, бесконечно близко к ней).

    Линия влияния Q3 строится аналогично линии влияния М3.

    При движении P=1 по участку DE левее точки 3, рассматривая равновесие левой отсечённой части (относительно точки 3) балки DN, имеем :

                      Q3=-P=-1

    Т.е. на участке DE линия влияния Q3 параллельна оси абсцисс.

    Для построения л.в. на участке AD поступим следующим образом : ординату точки D (y=-1) соединим с ординатой точки B (y=0) и продолжим до пересечения с ординатой точки А. Ординату точки А найдём из подобия треугольников : yA=2×1/4=0.5

    При движении P=1 по участку DE, правее точки 3, а также по участкам EN и NH, рассматривая равновесие левой отсечённой части балки DN, имеем Q3=0

    Линия влияния Q3 построена на рисунке 5.

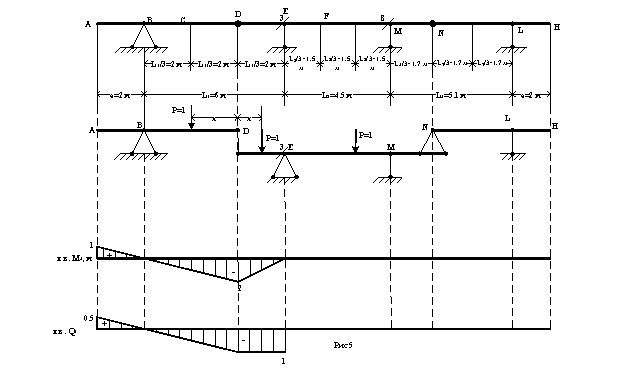
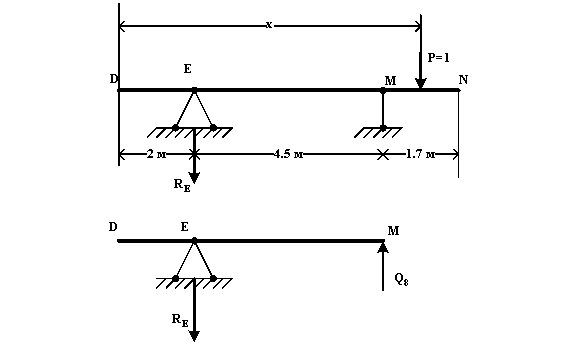
    Построение линии влияния изгибающего момента М8 в сечении 8 (левее точки М, бесконечно близко от неё).

    При движении P=1 по участку DM левее точки 8 и по участку AD – М8=0 (линия влияния совпадает с осью абсцисс). Это следует из рассмотрения равновесия правой отсечённой части MN :

                              M8=MM=RM·0=0

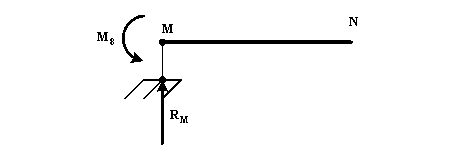
    При движении P=1 по участку MN правее точки 8, рассматривая равновесие правой отсечённой части MN балки DN, имеем :

               M8=RM·0-Px=-x

    при x=0 (точка М) – М8=0 ; при x=1.7 м (точка N) – M8=-1.7 м

    При движении P=1 по участку NH, рассматривая равновесие правой отсечённой части MN балки DN, имеем :

                               M8=-1.7RN

    где RN находим, рассматривая равновесие участка NH.

                          ΣmL=0 ; -3.4RN+P(5.1-x)=0  ;  RN= 

                            M8=

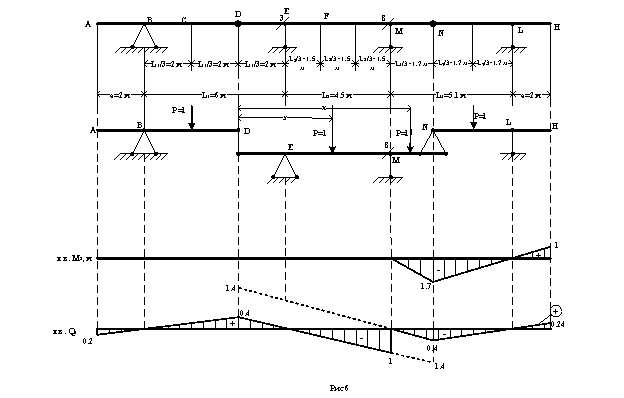
    при x=1.7 (точка N) – M8=-1.7 м ; при x=5.1 (точка L) – M8=0 ; при x=7.1 м (точка H) – M8=1 м.

    Линия влияния М8 построена на рисунке 6.

    Построение линии влияния поперечной силы Q8 в сечении 8 (левее точки М, бесконечно близко к ней).

    Линия влияния Q8 строится аналогично линии влияния М8.

    При движении P=1 по участку DM (с лево от точки 8), рассматривая равновесие правой отсечённой части (MN) балки DN, имеем :

                    Q8=-RM=

    где RM находим из уравнения равновесия, составленного для балки DN :

                   ΣME=0 ; -P(x-2)+4.5RM=0 ; RM=

    при x=0 (точка D) – Q8=0.4 ; при x=2 м (точка Е) – Q8=0 ; при x=6.5 м (точка M) – Q8=-1 ; при x=8.2 м (точка N) – Q8=-1.4

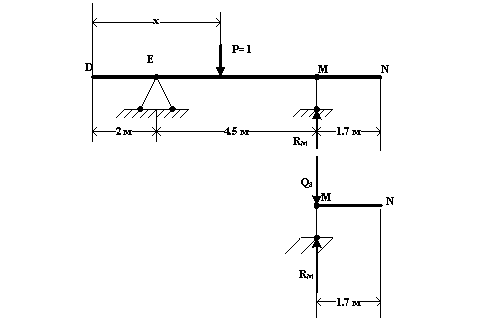
По полученным данным строим левую прямую л.в. Q8, при движении P=1 по балке DM.

    Для построения л.в., при движении P=1 по балке AD поступаем следующим образом : соединяем ординату точки D (0.4) с ординатой точки B (y=0) и, продолжаем эту прямую до пересечения с ординатой точки А. Ординату точки А находим из подобия треугольников : ; yA=2×0.4/4=0.2. Таким образом, левая прямая л.в. построена.

    При движении P=1 по участку MN (с право от точки 8), рассматривая равновесие левой отсечённой части (DM), балки DN, имеем :

                    Q8=-RE=

    где RE находим из уравнения равновесия, составленного для балки DN :

                     ΣmM=0 ; -P(x-6.5)+4.5RE=0 ; RE=  

    при x=0 (точка D) – Q8=1.4 ; при x=6.5 м (точка М) – Q8=0 ; при x=8.2 м (точка N) –

Q8= -0.4.

    По полученным данным строим правую прямую л.в. Q8, при движении P=1 по участку MN. Для построения л.в., при движении P=1 по балке NH поступаем следующим образом : соединяем ординату точки N (-0.4) с ординатой точки L (y=0) и, продолжаем эту прямую до пересечения с ординатой точки H. Ординату точки H найдём из подобия треугольников :    yH=2×0.4/3.4=0.24. Таким образом, правая прямая л.в. Q8 – построена. Линия влияния Q8 приведена на рисунке 6.

 

  

    6. Определение поперечной силы QE в сечении Е по линии влиянии от заданно нагрузки.

             QE=

    где y – ордината линии влияния под сечением с сосредоточенной нагрузкой P ; ω - площадь участка линии влияния под нагрузкой q ; α – угол наклона линии влияния в месте приложения сосредоточенного момента.

    Тогда (см. рисунок 7) :

             QE= кН

    На эпюре Q, при движении слева : QE=-20 кН