Ниже приведено фото задачи. Закачка решений(doc в архиве rar) начнется автоматически через 10 секунд. Если закачка не началась, кликните по этой ссылке. Еще примеры решения задач по строительной механике можно посмотреть здесь.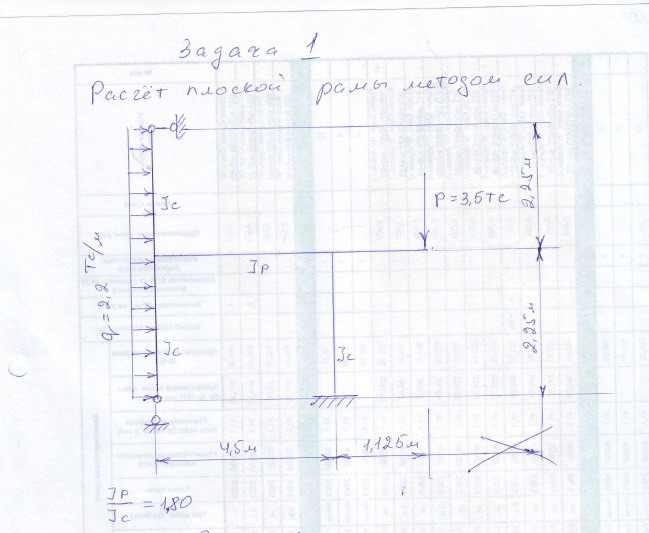
Скачать решение(в архиве rar):
Исходные данные:
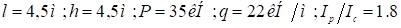
Решение:
1. Раму можно представить как конструкцию, состоящую их двух замкнутых контуров 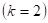 , в которые введено 4 простых шарнира
, в которые введено 4 простых шарнира 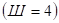 . Тогда степень статической неопределимости системы или число лишних неизвестных будет равно:
. Тогда степень статической неопределимости системы или число лишних неизвестных будет равно:
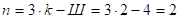
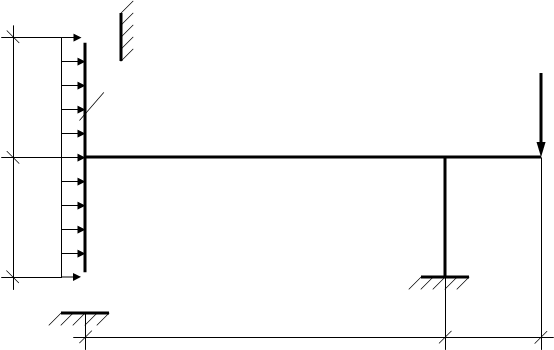
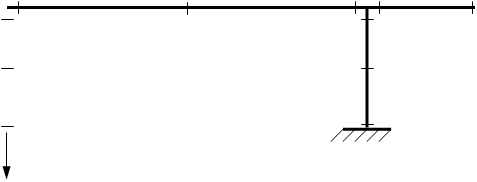
2. Чтобы получить основную статически определимую систему метода сил, достаточно из исходной системы удалить две лишние связи. Это можно сделать разными способами: убрать опорные стержни на стойке, оставив заделку; убрать один из опорных стержней, заменив одновременно заделку двумя опорными стержнями (шарниром): и т.д. Первый способ кажется более рациональным, поскольку позволяет строить в основной системе эпюры изгибающих моментов, не отыскивая предварительно опорные реакции. Этот способ мы и выбираем (рис.1б).
На схеме основной системы нумеруем характерные сечения рамы и
показываем неизвестные силы 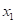 и
и 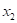 , которые заменяют нам отброшенные связи.
, которые заменяют нам отброшенные связи.
3. Система канонических уравнения метода сил для нашей рамы будет иметь вид:
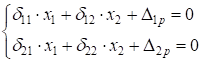
где 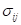 – перемещения основной системы в направлении действия силы
– перемещения основной системы в направлении действия силы 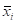 ; при действии на основную систему единичной силы
; при действии на основную систему единичной силы 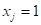 ;
;
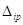 – перемещение основной системы в направлении действия силы
– перемещение основной системы в направлении действия силы 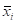 ; при действии на основную систему внешней нагрузки
; при действии на основную систему внешней нагрузки 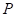 и
и 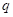 . Для определения
. Для определения 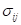 и
и 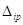 предварительно строим единичные и грузовые эпюры изгибающих моментов в основной системе. Эпюры строим со стороны растянутого волокна.
предварительно строим единичные и грузовые эпюры изгибающих моментов в основной системе. Эпюры строим со стороны растянутого волокна.
а) нагружаем основную систему силой 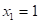 и получаем эпюру
и получаем эпюру 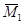 - рис.1в.;
- рис.1в.;
б) нагружаем основную систему силой 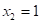 и получаем эпюру
и получаем эпюру 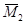 - рис.1.г;
- рис.1.г;
в) нагружаем основную систему силами 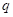 и
и 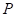 - получаем эпюру
- получаем эпюру 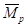 -рис.1.д
-рис.1.д
4. Значение коэффициентов канонических уравнений находим через произведение двух эпюр 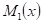 ,
, 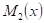 , заданных на отрезке
, заданных на отрезке 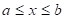 балки с моментом инерции
балки с моментом инерции 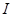 , равно:
, равно:
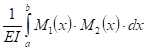
Мы, ввиду простой формы эпюр, будем пользоваться или правилом Верещагина, или, в более сложных случаях формулой Симпсона для каждого элементарного участка рамы, а само произведение эпюр будем обозначать через 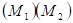
Теперь получаем:
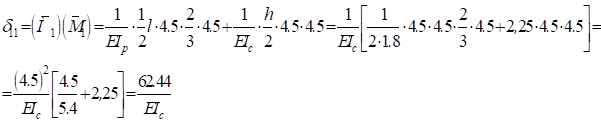
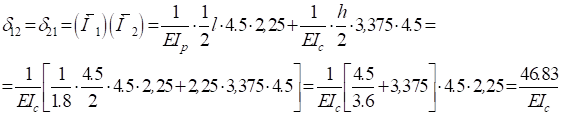
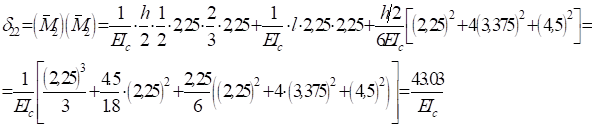
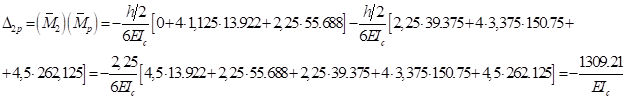
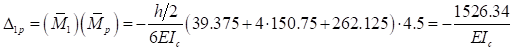
Таким образом имеем:
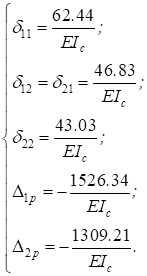
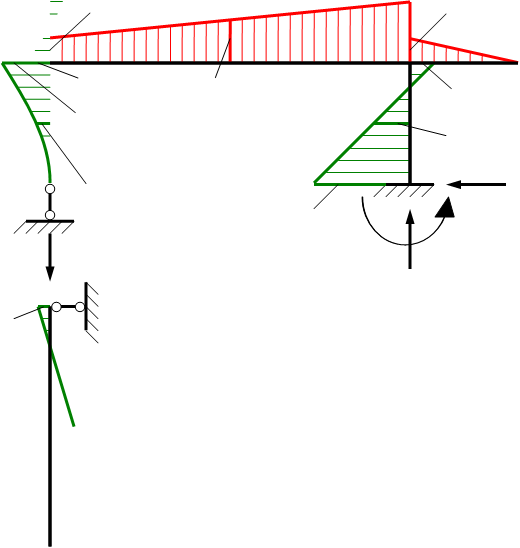
5. Проверим правильность подсчета коэффициентов. Для этого предварительно строим совместную единичную эпюру, когда на основную систему одновременно действуют силы:
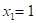 и
и 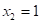 -
- 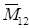 - рис.1.е.
- рис.1.е.
Должно быть:
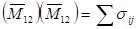 и
и 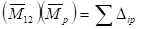
Проверим это:
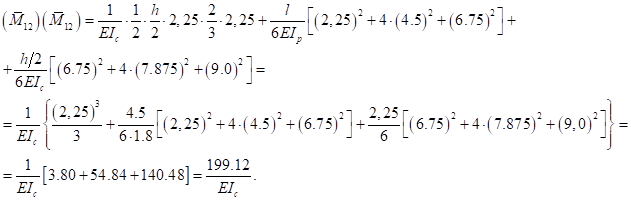
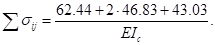
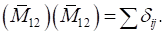
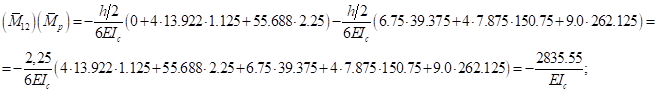
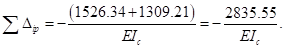
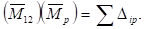
Коэффициенты найдены верно.
6. Подставляем их в канонические уравнения:
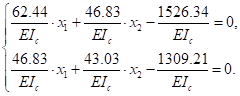
или
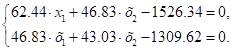
Решаем эту систему уравнений:
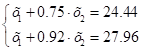
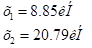
Проверим полученное решение подстановкой его в исходную систему уравнений:
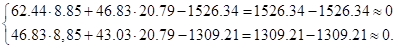
7. Строим окончательную эпюру изгибающих моментов М – рис.1.ж. Для ее построения вычисляем значения ее ординат в характерных сечениях рамы по правилу:
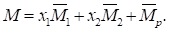
Получаем:

Проверяем правильность ее построения.
а) Статическая проверка.
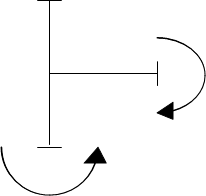
Проверяем равновесия узла 2-3-5.

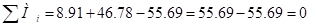 – узел находится в равновесии.
– узел находится в равновесии.

 Проверяем равновесие узла 6-7-8.
Проверяем равновесие узла 6-7-8.

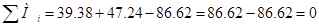 – узел находится в равновесии.
– узел находится в равновесии.
б) Деформационная проверка.
Т.к. перемещение сечений 4 и 1 в исходной системе равно нулю, то должно быть 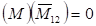
Проверяем это: 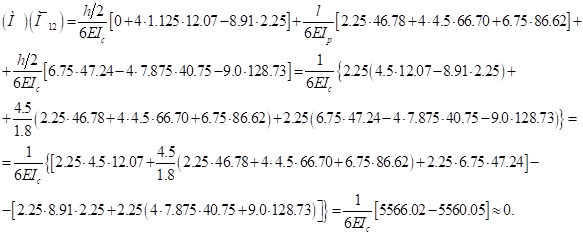 Невязка составлений:
Невязка составлений:
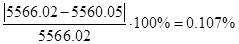
8. Строим эпюры 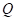 и
и 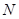
Для этого снова анализируем эпюру.
По стойке 1-2 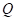 изменяется линейно от
изменяется линейно от 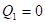 до
до 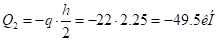
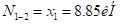 (за положительное направление берем растягивающие усилия). По стойке 4-3
(за положительное направление берем растягивающие усилия). По стойке 4-3 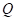 изменяется линейно оси
изменяется линейно оси 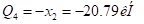 до
до 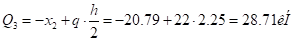
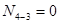
По ригелю 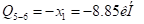
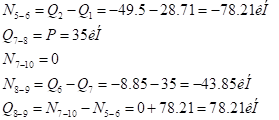
Отсюда находятся и реакции заделки:
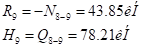
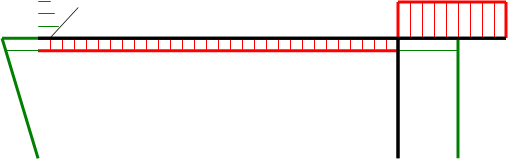
По этим данным строим эпюры 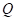 - рис.1.й. и
- рис.1.й. и  - рис.1.к.
- рис.1.к.
Проверяем устойчивость рамы в целом:
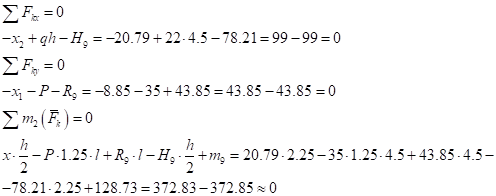
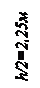
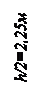






 а
а

б

 в
в



 г
г



 д
д


 е
е




 ж
ж





и




 к
к





 -
-




 +
+




 -
-

![]()
![]() , в которые введено 4 простых шарнира
, в которые введено 4 простых шарнира ![]() . Тогда степень статической неопределимости системы или число лишних неизвестных будет равно:
. Тогда степень статической неопределимости системы или число лишних неизвестных будет равно: ![]()
![]() и
и ![]() , которые заменяют нам отброшенные связи.
, которые заменяют нам отброшенные связи. 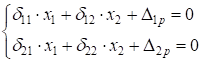
![]() – перемещения основной системы в направлении действия силы
– перемещения основной системы в направлении действия силы ![]() ; при действии на основную систему единичной силы
; при действии на основную систему единичной силы ![]() ;
; ![]() – перемещение основной системы в направлении действия силы
– перемещение основной системы в направлении действия силы ![]() ; при действии на основную систему внешней нагрузки
; при действии на основную систему внешней нагрузки ![]() и
и ![]() . Для определения
. Для определения ![]() и
и ![]() предварительно строим единичные и грузовые эпюры изгибающих моментов в основной системе. Эпюры строим со стороны растянутого волокна.
предварительно строим единичные и грузовые эпюры изгибающих моментов в основной системе. Эпюры строим со стороны растянутого волокна. ![]() и получаем эпюру
и получаем эпюру ![]() - рис.1в.;
- рис.1в.; ![]() и получаем эпюру
и получаем эпюру ![]() - рис.1.г;
- рис.1.г;![]() и
и ![]() - получаем эпюру
- получаем эпюру ![]() -рис.1.д
-рис.1.д![]() ,
, ![]() , заданных на отрезке
, заданных на отрезке ![]() балки с моментом инерции
балки с моментом инерции ![]() , равно:
, равно: 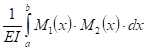
![]()
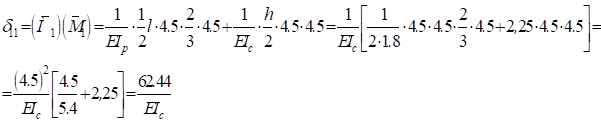
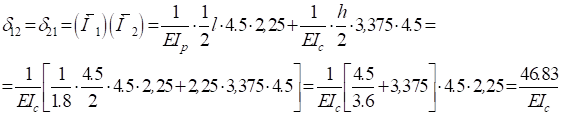
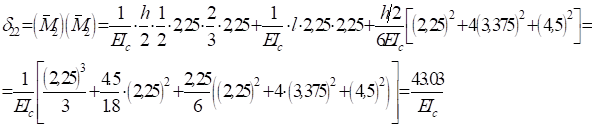
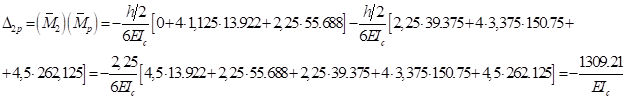
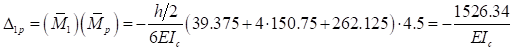
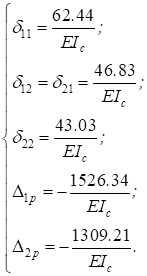
![]() и
и ![]() -
- ![]() - рис.1.е.
- рис.1.е. ![]() и
и ![]()
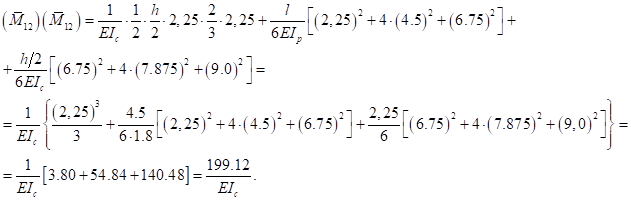
![]()
![]()
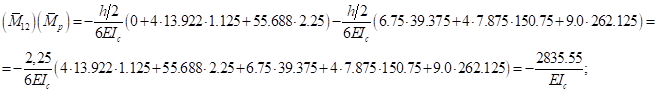
![]()
![]()
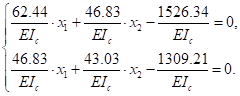
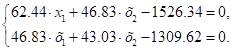
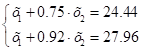
![]()
![]()
![]()


![]() – узел находится в равновесии.
– узел находится в равновесии. 
 Проверяем равновесие узла 6-7-8.
Проверяем равновесие узла 6-7-8.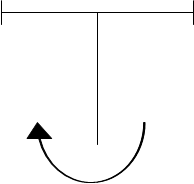
![]()
![]() – узел находится в равновесии.
– узел находится в равновесии. ![]()
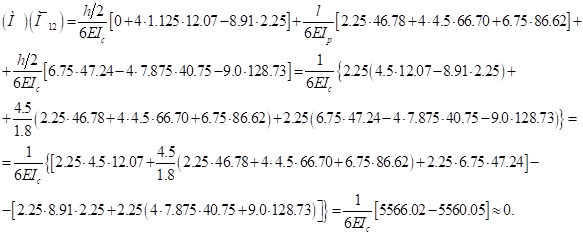 Невязка составлений:
Невязка составлений: ![]()
![]() и
и ![]()
![]() изменяется линейно от
изменяется линейно от ![]() до
до ![]()
![]() (за положительное направление берем растягивающие усилия). По стойке 4-3
(за положительное направление берем растягивающие усилия). По стойке 4-3 ![]() изменяется линейно оси
изменяется линейно оси ![]() до
до ![]()
![]()
![]()
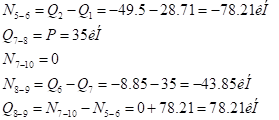
![]()
![]() - рис.1.й. и
- рис.1.й. и ![]() - рис.1.к.
- рис.1.к. 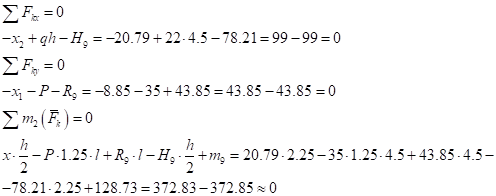

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() а
а 
![]()
![]()
![]() в
в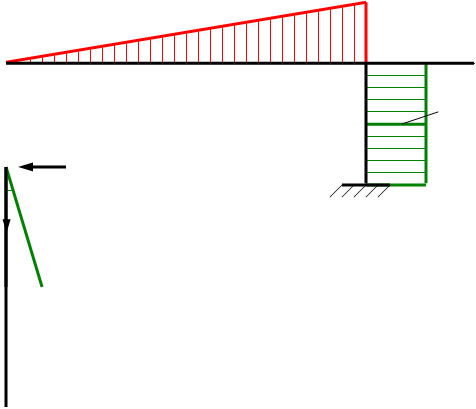
![]()
![]()
![]()
![]() г
г
![]()
![]()
![]()
![]()
![]()
![]() д
д 

![]()
![]()
![]() е
е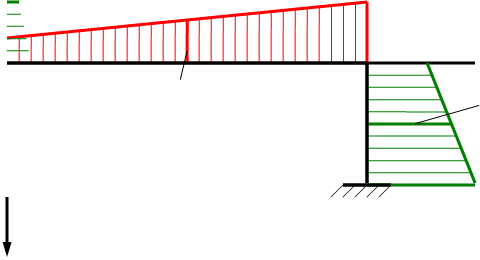

![]()
![]()
![]()
![]()
![]()
![]() ж
ж![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
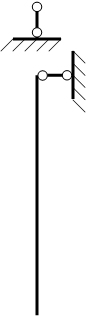
![]() к
к
![]()
![]()
![]()
![]()
![]()
![]() -
- 
![]()
![]()
![]()
![]()
![]() +
+ ![]()
![]()
![]()
![]()
![]() -
-
