Расчет статически неопределимой рамы методом сил

    Для рамы, выбранной согласно варианта, требуется :

    1. Используя индивидуальный шифр, выбрать : расчётную схему рамы, её размеры, жёсткость стержней, действующую нагрузку.

    2. Установить степень статической неопределимости и выбрать основную систему.

    3. Написать каноническое уравнение в общем виде.

    4. Построить в основной системе эпюры Mi от единичных сил и эпюру MF от заданной нагрузки.

    5. Найти коэффициенты и свободные члены канонических уравнений. Сделать проверку правильности нахождения их.

    6. Решить систему канонических уравнений и сделать проверку решения.

    7. Построить окончательную эпюру М. Выполнить статически и кинематическую проверки эпюры М.

    8. По окончательной эпюре М построить эпюру Q.

    9. По Q построить эпюру N.

    10. Выполнить статическую проверку равновесия системы в целом.

    Дано :

№ схемы	a,     м	b,     м	с,     м	d,     м	α	β	γ	F1,    кН	F2,   кН	q1,  кН/м	q2, кН/м
3	3.8	5.2	4.2	2.1	3	4	2	0	21	0	8

 

                                                                   Решение.

1. Расчётная схема.

    2. Установим степень статической неопределённости и выберем основную систему.

    Степень статической неопределимости (количество лишних связей определим по формуле :

             Л=2Ш+С0-3Д=2×0+5-3×1=2

    где Ш=0 – количество шарниров, соединяющих диски с учётом их кратности ; С0=5 – количество опорных стержней ; Д=1 – число дисков в системе.

    Основную систему (О.С.) примем, как показано на рисунке 1.

    3. Система канонических уравнений имеет вид :

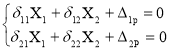                                                          (1)

    Коэффициенты при неизвестных и свободные члены канонических уравнений (1) определим по формулам :

             δii=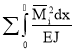  ;  δik=δki= 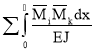 ;  Δip= 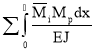         (2)

    4. Строим в основной системе эпюры Mi от единичных сил и эпюру MP от заданной нагрузки.

    На рисунке 2 приведена эпюра изгибающих моментов при нагружении основной системы силой X1=1

    Реакции опор : MH1=X1(2b+a)=14.2 м ; YH1=X1=1 м

    Участок AB : M1=0

    Участок BC : M2=0

    Участок BD : M3=X1x3, где 0<x3<a+b ; MB=0 ; MD=(a+b)X1=9 м

    Участок DE : M4=(a+b)X1 ; MD=ME=9 м

    Участок EF : M5=MH1-YH1x5, где 0<x5E=MH1-YH1b=14.2-5.2=9 м ;

                                                                           MF=MH1=14.2 м

    Участок FN : M6=0

    Участок FH : M7=MH1=14.2 м.

    На рисунке 2 приведена эпюра изгибающих моментов при нагружении основной системы силой X2=1.

    Реакции опор : XH2=X2=1 м

    Участок AB : M1=X2y1, где 0<y1<c+d ; MA=0 ; MB=X2(c+d)=6.3 м.

    Участок BC : M2=0

    Участок BD : M3=X2(c+d)=6.3 м

    Участок DE : M4=XH2y4, где c<y4<c+d ; MD=XH2(c+d)=6.3 м ; ME=XH2c=4.2 м

    Участок EF : M5=XH2c=4.2 м

    Участок FN : M6=0

    Участок FH : M7=XH2y7, где 0<y7<c ; MF=XH2c=4.2 м ; MH=0

 

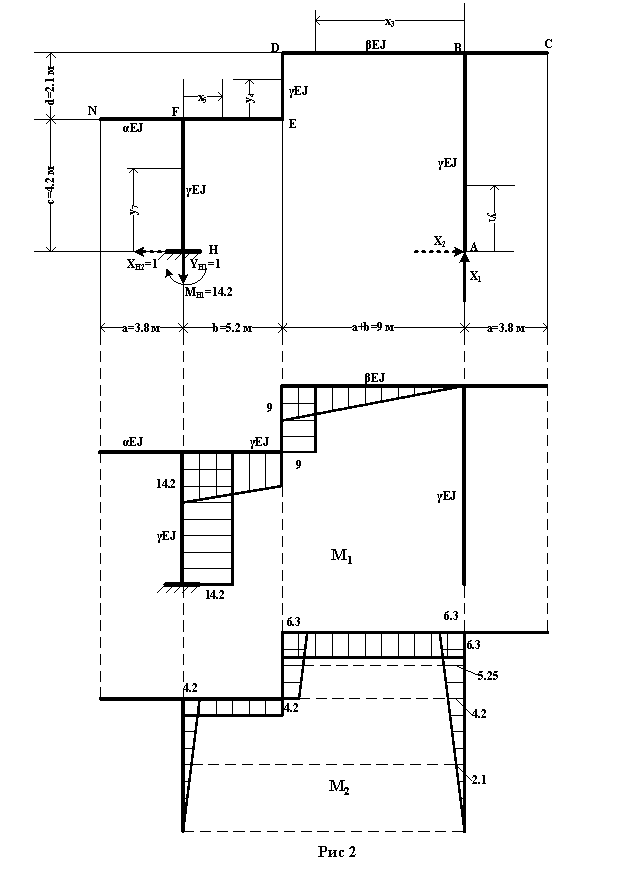
     На рисунке 3 приведена эпюра изгибающих моментов основной системы от заданной нагрузке.

    Реакции опор :  ΣmH=0 ;

                               MH+0.5q2a2-F2c+0.5q2(c+d)2-F2(2b+2a)=0

                                 MH=

                                кН·м

           ΣYk=0 ; YH-q2a-F2=0 ; YH=q2a+F2=8×3.8+21=51.4 кН

           ΣXk=0 ; XH+F2-q2(c+d)=0 ; XH=q2(c+d)-F2=8×(4.2+2.1)-21=29.4 кН

    Участок AB : M1=-0.5q2y12, где 0<y1<c+d ; MA=0 ;

                              MB=-0.5q2(c+d)2=-0.5×8×(4.2+2.1)2=-158.76 кН·м

    Участок BC : M2=-F2x2, где 0<x2<a ; MC=0 ; MB=-F2a=-21×3.8=-79.8 кН·м

    Участок BD : M3=-F2x3-0.5q2(c+d)2, где a<x3<2a+b ;

                 MB=-F2a-0.5q2(c+d)2=-21×3.8-0.5×8×(4.2+2.1)2=-238.56 кН·м ;

                 MD=-F2(2a+b)-0.5q2(c+d)2=-21×(2×3.8+5.2)-0.5×8×(4.2+2.1)2=-427.56 кН·м

    Участок DE : M4=-F2(2a+b)-0.5q2(c+d)2

                 MD=-F2(2a+b)-0.5q2(c+d)2=-21×(2×3.8+5.2)-0.5×8×(4.2+2.1)2=-427.56 кН·м

                 ME=-F2(2a+b)-q2(c+d)(0.5(c+d)-d)=-21×12.8-8×6.3×(0.5×6.3-2.1)=-321.72 кН·м

    Участок EF : M5=-q2a(x5+0.5a)+YHx5-XHc-MH, где 0<x5<b

                  ME=-q2a(b+0.5a)+YHb-XHc-MH=

                 =-8×3.8×(5.2+0.5×3.8)+51.4×5.2-29.4×4.2-249.68= -321.72 кН·м

                  MF=-0.5q2a2-XHc-MH=-0.5×8×3.82-29.4×4.2-249.68=-430.92 кН·м

    Участок FN : M6=-0.5q2x62, где 0<x6<a ; MN=0 ;

                   MF=-0.5×8×3.82=-57.76 кН·м

    Участок FH : M7=-XHy7-MH, где 0<y7<c ;

                   MF=-29.4×4.2-249.68=-373.16 кН·м

                   MH=-249.68 кН·м

    5. Найдём коэффициенты и свободные члены канонических уравнений. Сделаем проверку правильности нахождения их.

    Численные значения коэффициентов при неизвестных и свободных членов уравнений (1) найдём способом перемножения эпюр.

          EJδ11=

               =

              =60.75+85.05+237.143+423.444=806.387

           EJδ22=

     =

         =41.675+89.303+29.327+30.576+12.348=203.229

            EJδ12=EJδ21=

          

 

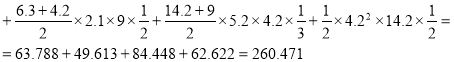
          EJΔ1p=

         

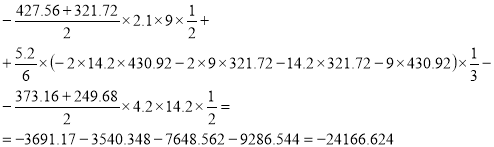
          EJΔ2p=

          

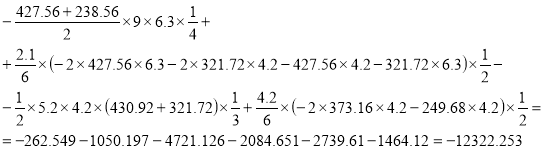
    Выполним построчные проверки правильности коэффициентов при неизвестных, пользуясь условием :

                              

    где - суммарная единичная эпюра изгибающих моментов, получаемая по зависимости , приведена на рисунке 4.

 

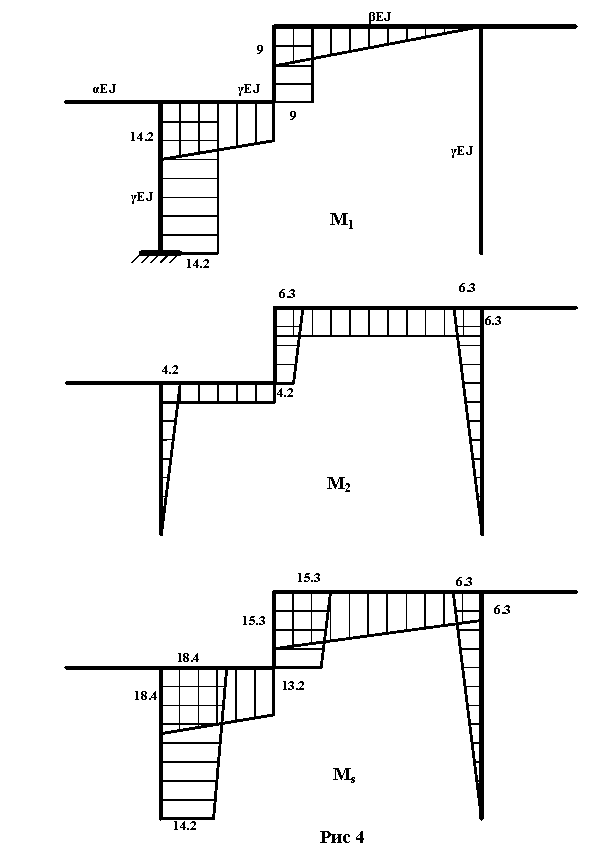
    Перемножение эпюр и выполним пользуясь правилом Верещагина.

           

           

         

            EJ(δ11+δ12)= 806.387+260.471=1066.858

           

           

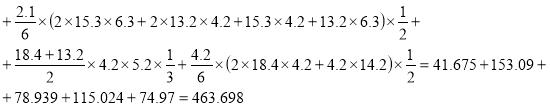
             EJ(δ22+δ21)=203.229+260.471=463.7

    Проверим правильность вычисления свободных членов уравнений (1) :

            

            

            

            

            

    =-262.549-1050.197-8412.296-5624.999-10388.172-10750.664=-36488.877

                EJ(Δ1p+Δ2p)=

    Следовательно, коэффициенты δ и Δ определены правильно.

    6. Решим систему канонических уравнений и сделаем проверку решения.

    Подставляя в систему (1) значения, полученных коэффициентов, получим систему :

                 

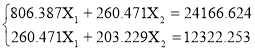
    Решим, полученную систему.

              Δ= ; Δ1=

              Δ2=

    Тогда : X1= кН ; X2= кН

    Проверку правильности решения системы уравнений произведём путём подстановки полученных значений X1 и X2 в исходные уравнения :

              

    Таким образом, реакции X1 и X2 найдены, верно.

    7. Построим окончательную эпюру М. Выполним статическую и кинематическую проверку эпюры М.

    Окончательная эпюра изгибающих моментов может быть получена по уравнению :

                          M=

    Эпюры изгибающих моментов от фактических значений X1 и X2 приведены на рисунке 5.

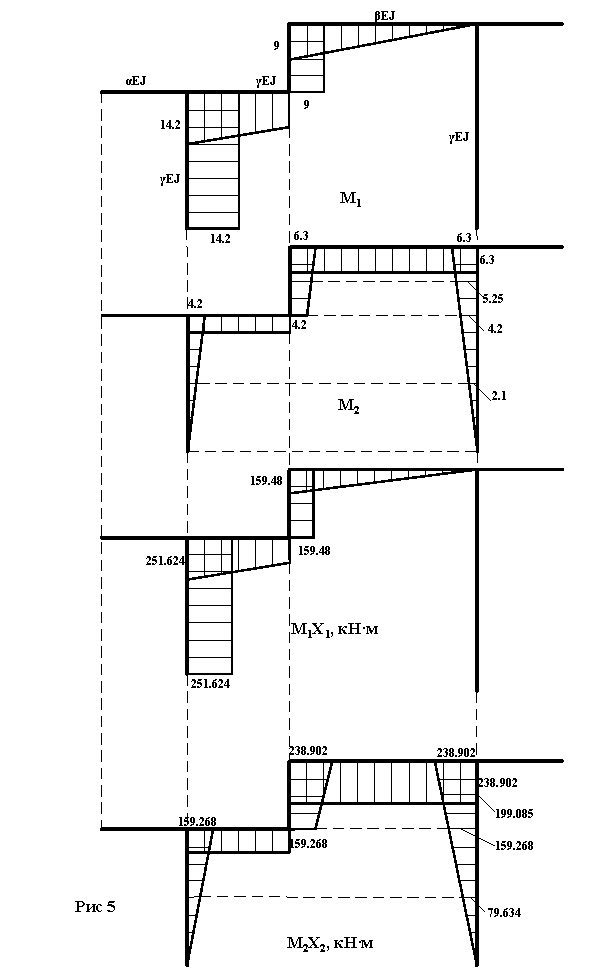
    Результирующая эпюра М построена на рисунке 6.

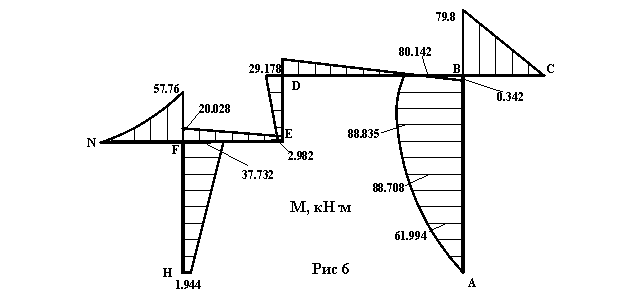
    Проведём проверку правильности окончательной эпюры изгибающих моментов.

    Статическая проверка состоит в том, что проверяем равновесие узла системы под действием изгибающих моментов, приложенных к примыкающим к узлу отсечённым стержням. При этом должно выполнятся условие : ΣMуз=0

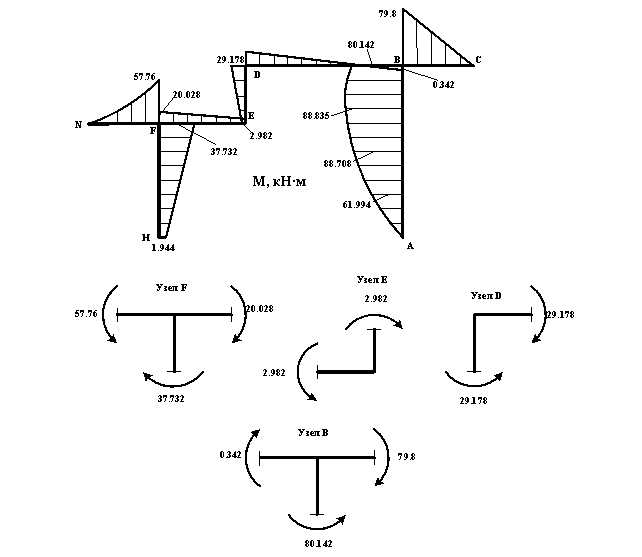
     Узел B : ΣMузB=-79.8-0.342+80.142=0

    Узел D :  ΣMузD=29.178-29.178=0

    Узел E :  ΣMузE=2.982-2.982=0

    Узел F :  ΣMузF=57.76-37.732-20.028=0

    Таким образом, равновесие рамы соблюдается.

    Кинематическую проверку выполним по условию :

                  

              

               

    Относительная погрешность вычислений :

                μ=

    Для стержневых систем средней сложности относительная погрешность вычислений должна составлять не более 3%.

    Статическая и кинематическая проверка выполняются, и, следовательно, окончательная эпюра изгибающих моментов построена – верно.

    8. Построение эпюры Q по эпюре М.

    Для построения эпюры поперечных сил воспользуемся окончательной эпюрой изгибающих моментов М.

    На участках, где эпюра М имеет прямолинейное очертание, поперечная сила численно равна :

                   Q=

    где α – угол наклона эпюры М к оси стержня.

    Если для совмещения с эпюрой изгибающих моментов стержень нужно поворачивать по ходу часовой стрелки, то поперечная сила принимается положительной.

    На участке BC : QBC=tgαBC=  кН

    На участке DB : QBD=tgαBD= кН

    На участке DE : QDE=tgαDE= кН

    На участке EF : QEF=tgαEF= кН

    На участке FH : QFH=tgαFH= кН

    На участках, где эпюра М ограничена параболой, поперечные силы найдём по формуле

                              Qx=                                   (3)

    где - значение поперечной силы в сечениях простой шарнирно опёртой балки.

    Определим поперечную силу Q на участке AB. Для этого определим , рассматривая участок AB как простую шарнирно опёртую балку.

   Реакции балки :

               ΣmB=0  ;  6.3HA-0.5q2·6.32=0  ;  HA=0.5×8×6.3=25.2 кН ; HB=25.2 кН

    На рисунке 7 построена эпюра . 

    Тогда, применяя формулу (3), получим :

                QA= кН

                 QB= кН

    Определим поперечную силу Q на участке FN. Для этого определим , рассматривая участок FN как простую шарнирно опёртую балку.

   Реакции балки :

               ΣmF=0  ;  -3.8VN+0.5q2·3.82=0  ;  VN=0.5×8×3.8=15.2 кН ; VF=15.2 кН

    На рисунке 7 построена эпюра . 

    Тогда, применяя формулу (3), получим :

                QN=

                 QF= кН

 

 

 

 

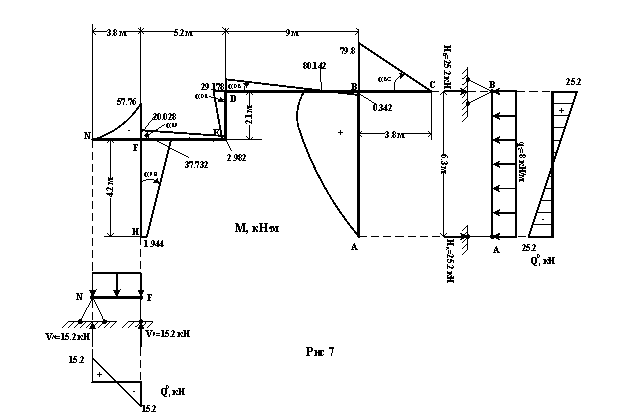
    Окончательная эпюра поперечных сил приведена на рисунке 8.

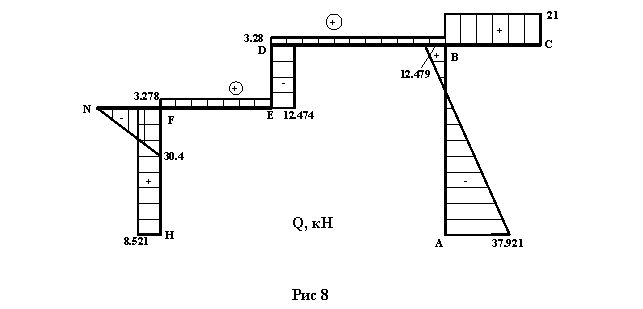
    9. По эпюре Q построим эпюру N.

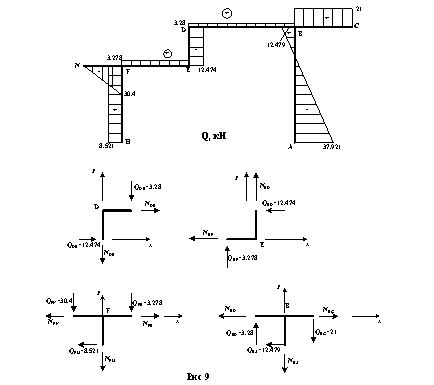
    Эпюру продольных сил N строим по эпюре поперечных сил Q, рассматривая равновесие узлов. Узлы рамы вырезаем в такой последовательности, чтобы каждый рассматриваемый узел содержал не более двух стержней с неизвестными продольными силами. При составлении уравнений равновесия (ΣX=0, ΣY=0) вначале полагаем, что все неизвестные продольные силы являются растягивающими (положительными). Отсечённые узлы рассматриваемой рамы приведены на рисунке 9.

    Узел D : ΣX=0 ; NDB+12.474=0  ;  NDB=-12.474 кН (стержень DB сжат)

                   ΣY=0 ; -NDE-3.28=0  ;  NDE=-3.28 кН (стержень DE сжат)

    Узел Е : ΣX=0 ; -NEF-12.474=0  ;  NEF=-12.474 кН (стержень EF сжат)

    Узел F : ΣX=0  ;  -NFN+NFE-8.521=0  ; NFN=0 (стержень FN не нагружен)

                  ΣY=0 ;   -NFH-30.4-3.278=0  ; NFH=-30.4-3.278=-33.678 кН (стержень FH сжат)

    Узел B : ΣX=0  ;  NBC-NBD-12.479=0 ; NBC=-12.479+12.479=0 (стержень BC не нагружен)

                   ΣY=0 ;  -NBA+3.28-21=0  ;  NBA=-21+3.28=-17.72 кН (стержень BA сжат)

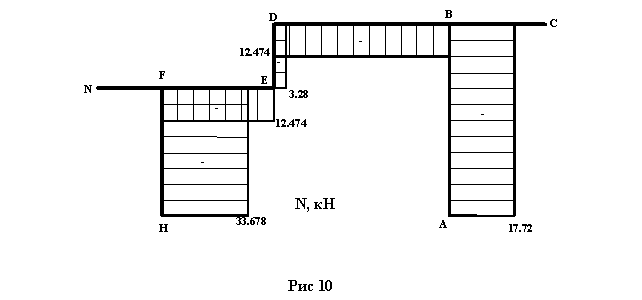
    Окончательная эпюра продольных сил N приведена на рисунке 10.

    10. Выполним статическую проверку равновесия системы в целом.

    По эпюрам Q, N и М из условий равновесия опорных узлов получены опорные реакции (рисунок 11) :

                   HH=8.521 кН ; VH=33.678 кН ; MH=1.944 кН·м ;

                   HA=37.921 кН ; VA=17.72 кН

    Для данной системы составляем три уравнения равновесия :

                  ΣX=0  ;  -HH+HA+F2-6.3q2=-8.521+37.921+21-6.3×8=58.921-58.921=0

                  ΣY=0  ;  VH+VA-F2-3.8q2=33.678+17.72-21-3.8×8=51.398-51.4=0

                  ΣmH=0 ;  -MH+0.5q2×3.82-4.2F2-18F2+0.5q2·6.32+14.2VA=0

                 -1.944+0.5×8×3.82-4.2×21-18×21+0.5×8×6.32+14.2×17.72=-468.144+468.144=0

    Таким образом, статические уравнения соблюдаются.