Пример решения задачи по строительной механике - расчет шпренгельной фермы
Ниже приведено решение задачи. Закачка решения в формате doc начнется автоматически через 10 секунд.

1. Исходные данные
Согласно задания: Неподвижная нагрузка: Постоянная нагрузка – узловая нагрузка F = 40 кН, приложенная к узлам верхнего и нижнего пояса, исключая опорные. Длинна панели d = 3,6 м . Высота t = 2,4 м. Исследуемые стержни – первая и вторая панель слева.
2. Кинематический анализ.
W=2У – Сф – Соп = 2 · 16 – 31 – 3 = 0,
Следовательно, ферма статически определима.
Здесь
У=16 – число узлов фермы, включая опорные;
Сф = 29 – число стержней фермы;
Соп = 3 – число опорных связей.
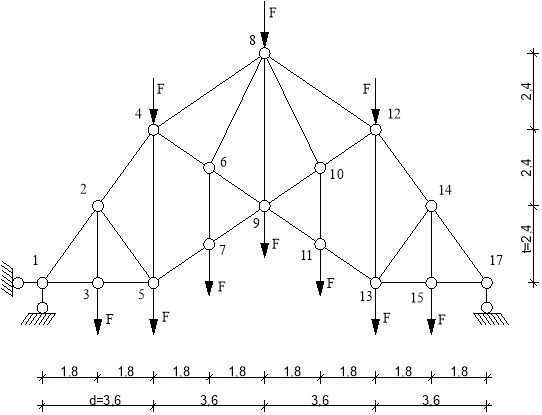
Рис.1
3. Определение опорных реакций от неподвижной нагрузки.
Поскольку ферма симметрична и нагружена симметричной нагрузкой:
![]()
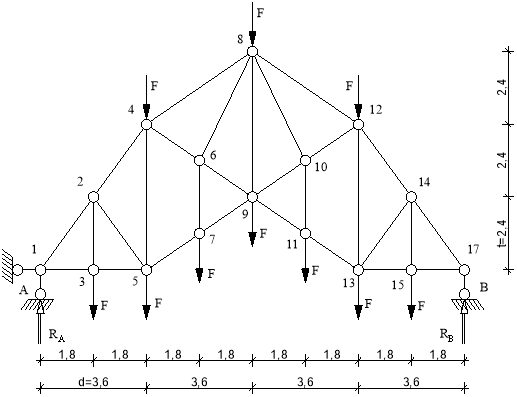
Рис.2 Расчетная схема заданной фермы.
4. Определение усилий в стержнях фермы. (аналитически)
Стержни шпренгельной фермы бывают трех категорий
- Стержни принадлежат только основной ферме. Усилия в этих стержнях определяются расчетом только основной фермы.
В нашей ферме – это исследуемые стержни (2-4, 4-5, 5-7, 7-9, 6-9, 8-9).
- Стержни принадлежащие одновременно, как основной ферме, так и дополнительной (шпренгелю). Усилия в этих стержнях определяются как сумма двух усилий. Одно усилие, возникающее в стержне основной фермы, второе – в слившемся с ним шпренгеле.
В нашей ферме – это исследуемые стержни (1-3, 1-2, 3-5, 4-6, 4-8).
3. Стержни принадлежащие только дополнительной ферме (шпренгелю).
Шпренгель рассматриваем как самостоятельную двухопорную ферму.
Усилие в этих стержнях определяется только от нагрузки приложенной
непосредственно к шпренгелю.
В нашей ферме – это исследуемые стержни (2-3, 2-5, 6-7, 6-8).
Разделим ферму на основную и дополнительные (шпренгели).
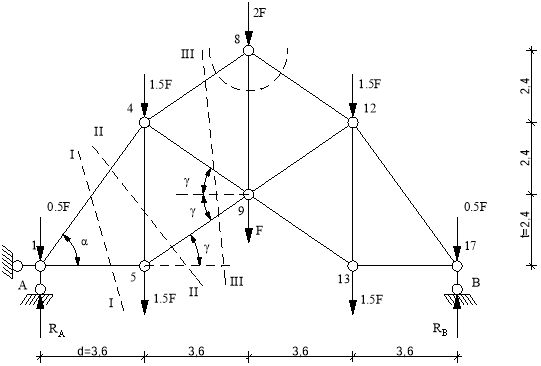
Рис.3. Основная ферма.
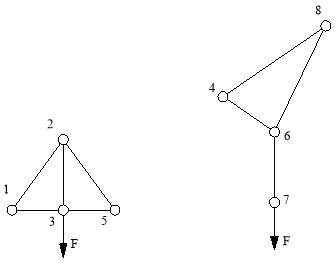
Рис.4. Дополнительные фермы (шпренгели).
Определим усилия в основной ферме.
Предварительно определим функции углов в ферме.
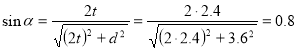
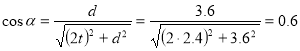
![]()
![]()
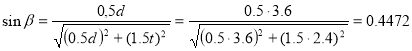
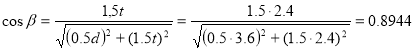
Усилие в стержне (1-4). Усилие находим методом сечений. Рассекаем ферму (сечение I-I)(рис.3) и рассматриваем равновесие левой части фермы. Составим уравнение равновесия относительно моментной точки 5.(рис. 5).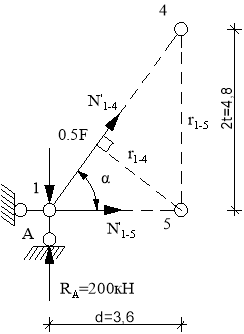
Рис.5
Плечо силы ![]() относительно т. 5:
относительно т. 5:
![]()
![]()
![]()
Усилие в стержне 1-5. Усилие находим методом сечений. Рассекаем ферму (сечение I-I)(рис.3) и рассматриваем равновесие левой части фермы. Составим уравнение равновесия относительно моментной точки 4. (рис5).
Плечо силы ![]() относительно т. 4:
относительно т. 4:
![]()
![]()
![]()
Усилие в стержне 4-5)’. Усилие находим методом сечений. Рассекаем ферму (сечение II-II)(рис.3) и рассматриваем равновесие левой части фермы. Составим уравнение равновесия относительно моментной точки С.(рис. 6).
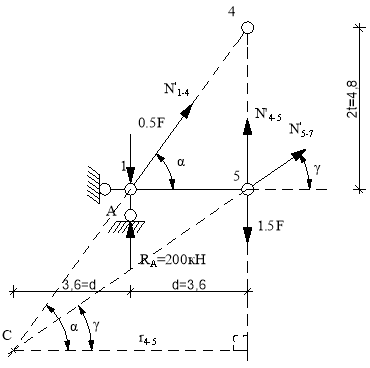
Рис.6
Плечо силы ![]() относительно т. С:
относительно т. С:
![]()
![]()
![]()
Усилие в стержне 4-9’. Усилие находим методом сечений. Рассекаем ферму (сечение III-III)(рис.3) и рассматриваем равновесие левой части фермы. Составим уравнение равновесия относительно оси У. (рис.7).
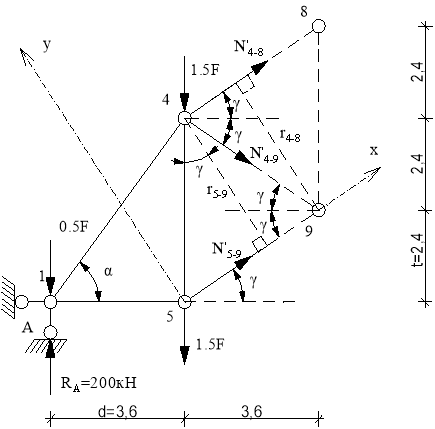
Рис.7
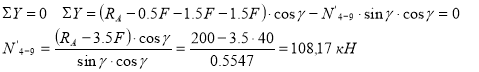
Усилие в стержне 5-9’. Усилие находим методом сечений. Рассекаем ферму (сечение III-III)(рис.3) и рассматриваем равновесие левой части фермы. Составим уравнение равновесия относительно моментной точки 4.(рис. 7).
Плечо силы ![]() относительно т. 4:
относительно т. 4:
![]()
![]()
![]()
Усилие в стержне 4-8’. Усилие находим методом сечений. Рассекаем ферму (сечение III-III)(рис.3) и рассматриваем равновесие левой части фермы. Составим уравнение равновесия относительно моментной точки 9.(рис. 7).
Плечо силы ![]() относительно т. 9:
относительно т. 9:
![]()
![]()
![]()
Усилие в стержне 8-9’. Усилие находим методом сечений. Вырезаем узел 8 (рис.3) и рассматриваем его равновесие. Составим уравнение равновесия относительно осей хОу. (рис.8).
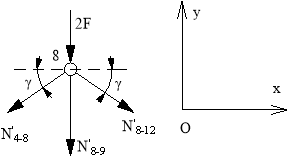
Рис.8
![]()
![]()
![]()
Определим усилия в стержнях дополнительной фермы.
Из заданной расчетной схемы (рис.2) выделим шпренгель первой панели слева (рис.9.1.).
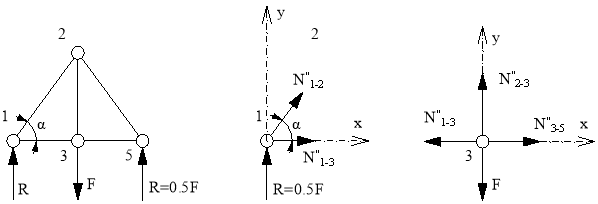
Рис.9.1. Рис.9.2. Рис.9.3.
Рассмотрим его как ферму на двух опорах ( опоры – узлы 1 и 5).
![]()
Усилие в стержне 1-2”(2-5”). Усилие находим методом сечений. Вырезаем узел 1 и рассматриваем его равновесие. Составим уравнение равновесия относительно осей хОу. (рис.9.2.).
![]()
![]()
Усилие в стержне 1-3”(3-5”). Усилие находим методом сечений. Вырезаем узел 1 и рассматриваем его равновесие. Составим уравнение равновесия относительно осей хОу. (рис.9.2.).
![]()
![]()
Усилие в стержне 2-3”. Усилие находим методом сечений. Вырезаем узел 3 и рассматриваем его равновесие. Составим уравнение равновесия относительно осей хОу. (рис.9.3.).
![]()
![]()
Из заданной расчетной схемы (рис.2) выделим шпренгель второй панели слева (рис.10.1.).
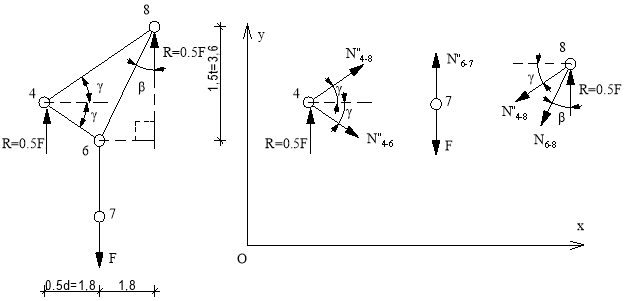
Рис.10.1. Рис.10.2. Рис.10.3. Рис.10.4.
Усилие в стержне 4-8”, 4-6”. Усилия находим методом сечений. Вырезаем узел 4 и рассматриваем его равновесие. Составим уравнения равновесия относительно осей хОу. (рис.10.2.).
![]()
![]()
![]()
Тогда, ![]()
Усилие в стержне 6-7”. Усилие находим методом сечений. Вырезаем узел 7 и рассматриваем его равновесие. Составим уравнение равновесия относительно оси у. (рис.10.3.).
![]()
Усилие в стержне 6-8”. Усилие находим методом сечений. Вырезаем узел 8 и рассматриваем его равновесие. Составим уравнение равновесия относительно оси у. (рис.10.4.).
![]()
![]()
Определим усилия в заданной расчетной схеме.
|
Стержень |
Основная ферма |
Шпренгель |
Заданная ферма |
|
1-3 |
135 |
15 |
150 |
|
3-5 |
135 |
15 |
150 |
|
1-2 |
-225 |
-25 |
-250 |
|
2-4 |
-225 |
- |
-225 |
|
2-3 |
- |
40 |
40 |
|
2-5 |
- |
-25 |
-25 |
|
4-5 |
-30 |
- |
-30 |
|
5-7 |
162,41 |
- |
162,41 |
|
7-9 |
162,41 |
- |
162,41 |
|
4-6 |
108,17 |
18,03 |
126,2 |
|
6-9 |
108,17 |
- |
108,17 |
|
4-8 |
-216,54 |
-18,03 |
-234,57 |
|
6-7 |
- |
40 |
40 |
|
6-8 |
- |
14,28 |
14,28 |
|
8-9 |
160,23 |
- |
160,23 |
6. Построение линий влияния.
Линии влияния для полной фермы строим как геометрическую сумму линии влияния основной фермы и линии влияния от дополнительной фермы (шпренгеля).
Линия влияния усилия в опоре А.
Груз на опоре А ![]()
Груз на опоре В ![]()
Над опорой А откладываем единицу и соединяем с нулем над опорой В.
Получили линию влияния усилия в опоре 17.
Линия влияния усилия в опоре В.
Груз на опоре А ![]()
Груз на опоре В ![]()
Над опорой В откладываем единицу и соединяем с нулем над опорой А.
Получили линию влияния усилия в опоре В.
Линия влияния N1-2.
Основная ферма.
Используем метод сечений. Рассекаем ферму (сечение I-I) Составим уравнение равновесия относительно моментной точки 5.(рис. 11).
Груз справа. Рассматриваем равновесие левой части фермы (рис.11). Составляем уравнение равновесия – сумма моментов относительно моментной точки 5.
![]()
![]()
То есть линия влияния ![]() представляет собой линию влияния усилия реакции RA, все ординаты которой умножены на (-1,25). Над опорой А откладываем (-1,25), соединяем с нулем над опорой В.
представляет собой линию влияния усилия реакции RA, все ординаты которой умножены на (-1,25). Над опорой А откладываем (-1,25), соединяем с нулем над опорой В.
Получили правую ветвь линии влияния усилия ![]() .
.
Груз слева. Рассматриваем равновесие правой части фермы (рис.11). Составляем уравнение равновесия – сумма моментов относительно моментной точки 5.
![]()
![]()
То есть линия влияния ![]() представляет собой линию влияния усилия реакции RB, все ординаты которой умножены на (-3.75). Над опорой В откладываем
представляет собой линию влияния усилия реакции RB, все ординаты которой умножены на (-3.75). Над опорой В откладываем
(-3,75), соединяем с нулем над опорой А.
Получена левая ветвь линии влияния ![]() .
.
Строим передаточную прямую, расположенную под рассеченной панелью. Левый узел 1 рассеченной панели сносим на левую ветвь, правый узел 4 на правую ветвь. Соединяем эти точки и получаем передаточную прямую.
Ветви пересекаются под моментной точкой 5.
Шпренгель.
Из заданной расчетной схемы (рис.2) выделим шпренгель первой панели
слева (рис.9.1.). Усилие находим методом сечений. Вырезаем узел 1 и рассматриваем его равновесие. Составим уравнение равновесия относительно оси у. (рис.9.2.).
Единичная сила в узле 1. ![]()
Единичная сила в узле 5. ![]()
Единичная сила в узле 3.
![]()
![]()
Геометрически суммируем линии влияния основной и дополнительной ферм.
Определение значения усилия по линиям влияния.
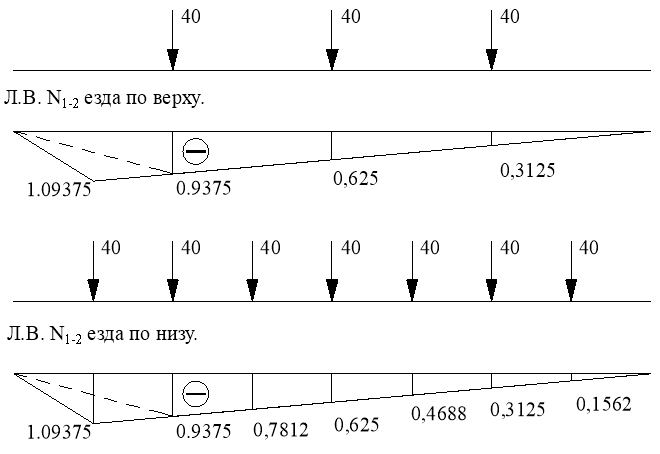
![]()
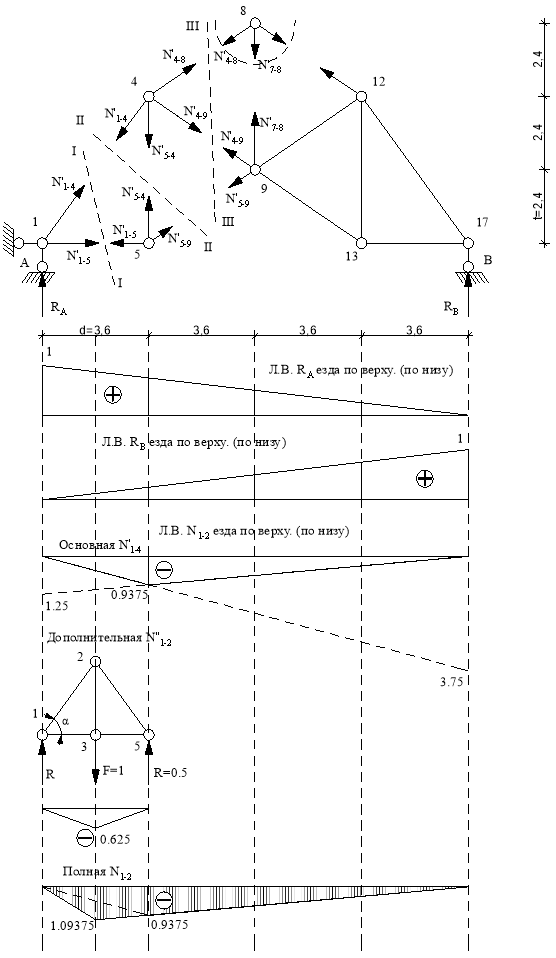 Рис.11
Рис.11
Линия влияния N2-4.
Основная ферма.
Используем метод сечений. Рассекаем ферму (сечение I-I) Составим уравнение равновесия относительно моментной точки 5.(рис. 12).
Груз справа. Рассматриваем равновесие левой части фермы (рис.12). Составляем уравнение равновесия – сумма моментов относительно моментной точки 5.
![]()
![]()
То есть линия влияния ![]() представляет собой линию влияния усилия реакции RA, все ординаты которой умножены на (-1,25). Над опорой А откладываем (-1,25), соединяем с нулем над опорой В.
представляет собой линию влияния усилия реакции RA, все ординаты которой умножены на (-1,25). Над опорой А откладываем (-1,25), соединяем с нулем над опорой В.
Получили правую ветвь линии влияния усилия ![]() .
.
Груз слева. Рассматриваем равновесие правой части фермы (рис.12). Составляем уравнение равновесия – сумма моментов относительно моментной точки 5.
![]()
![]()
То есть линия влияния ![]() представляет собой линию влияния усилия реакции RB, все ординаты которой умножены на (-3.75). Над опорой В откладываем
представляет собой линию влияния усилия реакции RB, все ординаты которой умножены на (-3.75). Над опорой В откладываем
(-3,75), соединяем с нулем над опорой А.
Получена левая ветвь линии влияния ![]() .
.
Строим передаточную прямую, расположенную под рассеченной панелью. Левый узел 1 рассеченной панели сносим на левую ветвь, правый узел 4 на правую ветвь. Соединяем эти точки и получаем передаточную прямую.
Ветви пересекаются под моментной точкой 5.
Шпренгель.
Стержень 2-4 принадлежит только основной ферме.
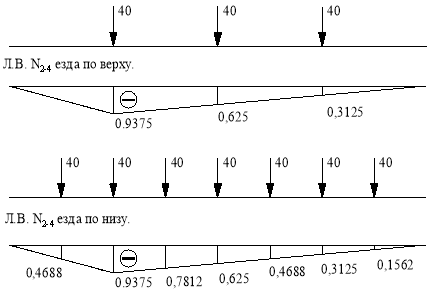
![]()
Линия влияния N2-5.
Основная ферма.
Стержень 2-5 принадлежит только шпренгелю.
Шпренгель.
Из заданной расчетной схемы (рис.2) выделим шпренгель первой панели
слева (рис.9.1.). Усилие находим методом сечений. Вырезаем узел 5 и рассматриваем его равновесие. Составим уравнение равновесия относительно оси у. (рис.9.2.).
Единичная сила в узле 1. ![]()
Единичная сила в узле 5. ![]()
Единичная сила в узле 3.
![]()
![]()
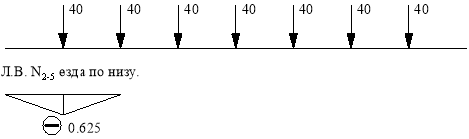
![]()
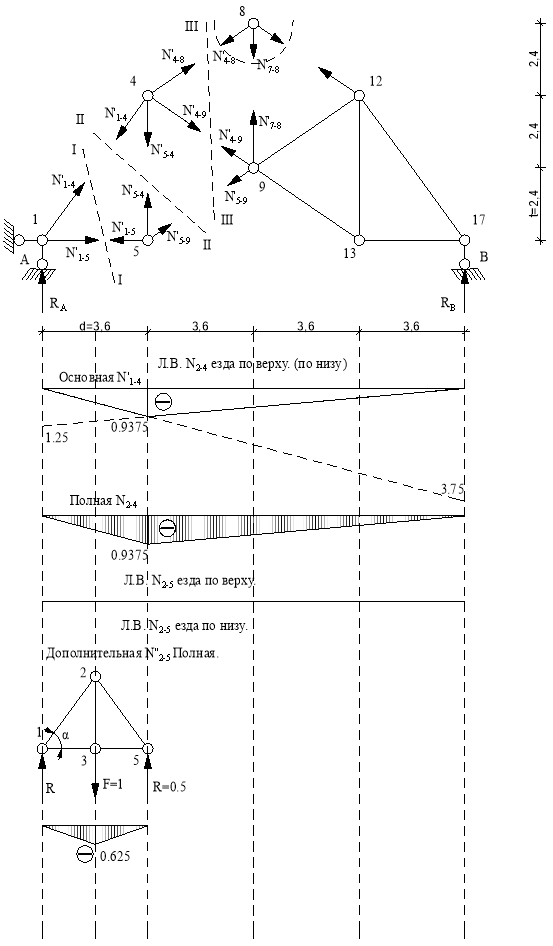 Рис.12
Рис.12
Линия влияния N1-3(N3-5).
Основная ферма.
Используем метод сечений. Рассекаем ферму (сечение I-I) Составим уравнение равновесия относительно моментной точки 4.(рис. 13).
Груз справа. Рассматриваем равновесие левой части фермы (рис.13). Составляем уравнение равновесия – сумма моментов относительно моментной точки 4.
![]()
![]()
То есть линия влияния ![]() представляет собой линию влияния усилия реакции RA, все ординаты которой умножены на (0.75). Над опорой А откладываем (0.75), соединяем с нулем над опорой В.
представляет собой линию влияния усилия реакции RA, все ординаты которой умножены на (0.75). Над опорой А откладываем (0.75), соединяем с нулем над опорой В.
Получили правую ветвь линии влияния усилия ![]() .
.
Груз слева. Рассматриваем равновесие правой части фермы (рис.13). Составляем уравнение равновесия – сумма моментов относительно моментной точки 4.
![]()
![]()
То есть линия влияния ![]() представляет собой линию влияния усилия реакции RB, все ординаты которой умножены на (2.25). Над опорой В откладываем
представляет собой линию влияния усилия реакции RB, все ординаты которой умножены на (2.25). Над опорой В откладываем
(2.25), соединяем с нулем над опорой А.
Получена левая ветвь линии влияния ![]() .
.
Строим передаточную прямую, расположенную под рассеченной панелью. Левый узел 1 рассеченной панели сносим на левую ветвь, правый узел 4 на правую ветвь. Соединяем эти точки и получаем передаточную прямую.
Ветви пересекаются под моментной точкой 4.
Шпренгель.
Из заданной расчетной схемы (рис.2) выделим шпренгель первой панели
слева (рис.9.1.). Усилие находим методом сечений. Вырезаем узел 1 и рассматриваем его равновесие. Составим уравнение равновесия относительно оси у. (рис.9.2.).
Единичная сила в узле 1. ![]()
Единичная сила в узле 5. ![]()
Единичная сила в узле 3.
![]()
Учитывая что ![]()
![]()
Геометрически суммируем линии влияния основной и дополнительной ферм.
Определение усилия по линиям влияния
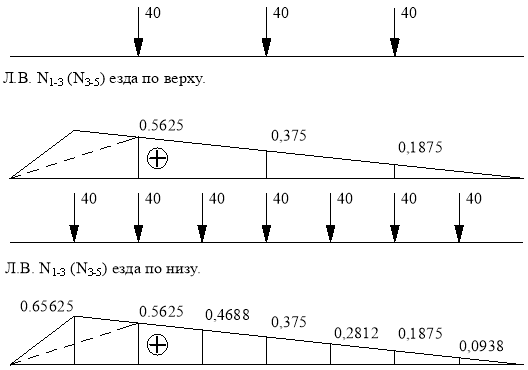
![]()
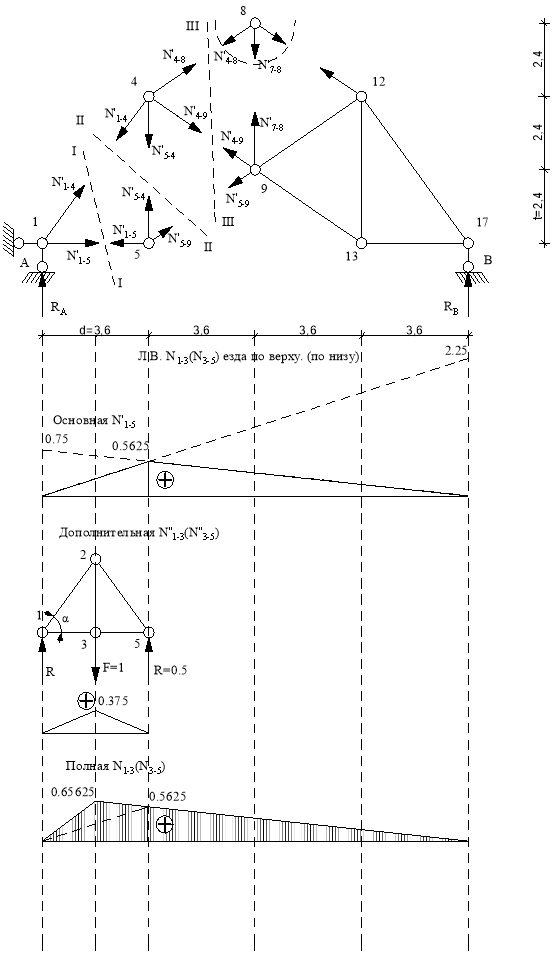 Рис.13
Рис.13
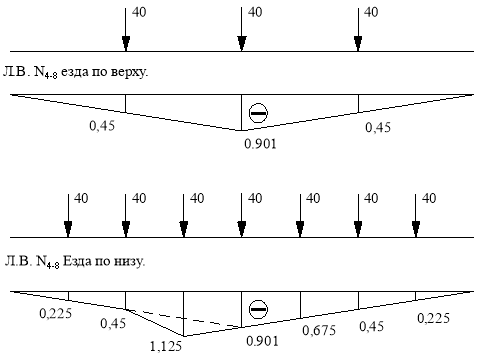
Линия влияния N4-5.
Основная ферма.
Используем метод сечений. Рассекаем ферму (сечение II-II) Составим уравнение равновесия относительно моментной точки C.(рис. 14).
Груз справа. Рассматриваем равновесие левой части фермы (рис.14). Составляем уравнение равновесия – сумма моментов относительно моментной точки 4.
![]()
![]()
То есть линия влияния ![]() представляет собой линию влияния усилия реакции RA, все ординаты которой умножены на (-0,5). Над опорой А откладываем (-0,5), соединяем с нулем над опорой В.
представляет собой линию влияния усилия реакции RA, все ординаты которой умножены на (-0,5). Над опорой А откладываем (-0,5), соединяем с нулем над опорой В.
Получили правую ветвь линии влияния усилия ![]() .
.
Груз слева. Рассматриваем равновесие правой части фермы (рис.14). Составляем уравнение равновесия – сумма моментов относительно моментной точки C.
![]()
![]()
То есть линия влияния ![]() представляет собой линию влияния усилия реакции RB, все ординаты которой умножены на (2,5). Над опорой В откладываем (2,5), соединяем с нулем над опорой А.
представляет собой линию влияния усилия реакции RB, все ординаты которой умножены на (2,5). Над опорой В откладываем (2,5), соединяем с нулем над опорой А.
Получена левая ветвь линии влияния ![]() .
.
Передаточная прямая при езде по верху.
Строим передаточную прямую, расположенную под рассеченной панелью. Левый узел 2 рассеченной панели сносим на левую ветвь, правый узел 4 на правую ветвь. Соединяем эти точки и получаем передаточную прямую.
Ветви пересекаются под моментной точкой С.
Передаточная прямая при езде по низу.
Строим передаточную прямую, расположенную под рассеченной панелью. Левый узел 5 рассеченной панели сносим на левую ветвь, правый узел 7 на правую ветвь. Соединяем эти точки и получаем передаточную прямую.
Ветви пересекаются под моментной точкой С.
Шпренгель.
Стержень 4-5 принадлежит только основной ферме.
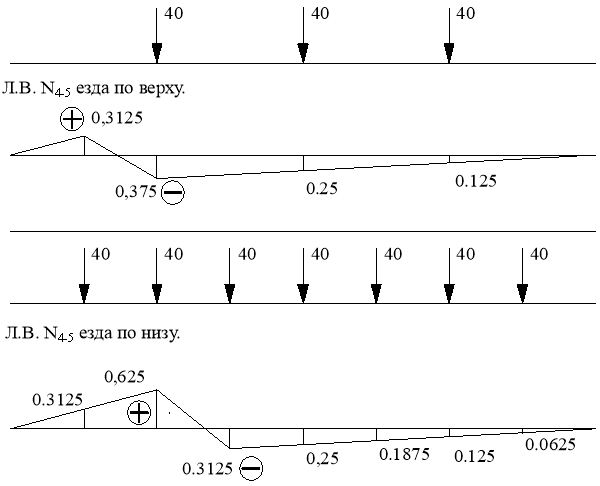
![]()
Линия влияния N2-3.
Основная ферма.
Стержень 2-3 принадлежит только шпренгелю.
Шпренгель.
Из заданной расчетной схемы (рис.2) выделим шпренгель первой панели
слева (рис.9.1.). Усилие находим методом сечений. Вырезаем узел 3 и рассматриваем его равновесие. Составим уравнение равновесия относительно оси у. (рис.9.2.).
Единичная сила в узле 1. ![]()
Единичная сила в узле 5. ![]()
Единичная сила в узле 3.
![]()
![]()
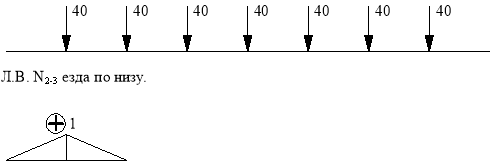
![]()
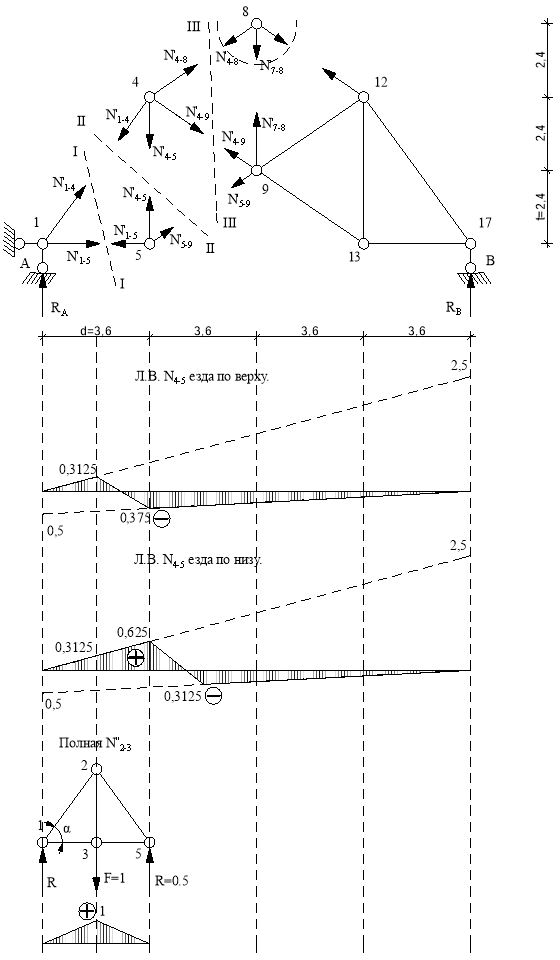 Рис.14
Рис.14
Линия влияния N5-7(N7-9).
Основная ферма.
Используем метод сечений. Рассекаем ферму (сечение III-III) Составим уравнение равновесия относительно моментной точки 4.(рис. 15).
Груз справа. Рассматриваем равновесие левой части фермы (рис.15). Составляем уравнение равновесия – сумма моментов относительно моментной точки 4.
![]()
![]()
То есть линия влияния ![]() представляет собой линию влияния усилия реакции RA, все ординаты которой умножены на (0.902). Над опорой А откладываем (0.902), соединяем с нулем над опорой В.
представляет собой линию влияния усилия реакции RA, все ординаты которой умножены на (0.902). Над опорой А откладываем (0.902), соединяем с нулем над опорой В.
Получили правую ветвь линии влияния усилия ![]() .
.
Груз слева. Рассматриваем равновесие правой части фермы (рис.15). Составляем уравнение равновесия – сумма моментов относительно моментной точки 4.
![]()
![]()
То есть линия влияния ![]() представляет собой линию влияния усилия реакции RB, все ординаты которой умножены на (2,707). Над опорой В откладываем
представляет собой линию влияния усилия реакции RB, все ординаты которой умножены на (2,707). Над опорой В откладываем
(2,707), соединяем с нулем над опорой А.
Получена левая ветвь линии влияния ![]() .
.
Строим передаточную прямую, расположенную под рассеченной панелью. Левый узел 5 рассеченной панели сносим на левую ветвь, правый узел 9 на правую ветвь. Соединяем эти точки и получаем передаточную прямую.
Ветви пересекаются под моментной точкой 4.
Шпренгель.
Стержень 5-7(7-9) принадлежит только основной ферме.
Определение усилия по линиям влияния
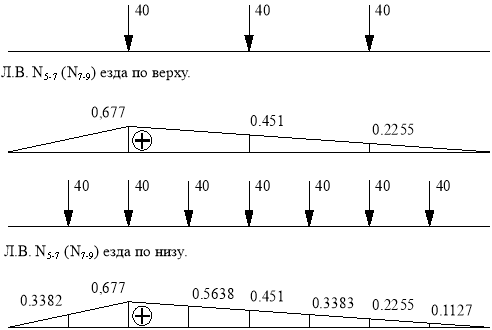
![]()
Линия влияния N6-7.
Основная ферма.
Стержень 6-7 принадлежит только шпренгелю.
Шпренгель.
Из заданной расчетной схемы (рис.2) выделим шпренгель второй панели
слева (рис.10.1.). Усилие находим методом сечений. Вырезаем узел 7 и рассматриваем его равновесие. Составим уравнение равновесия относительно оси у. (рис.10.3.).
Единичная сила в узле 5. ![]()
Единичная сила в узле 9. ![]()
Единичная сила в узле 3.
![]()
![]()
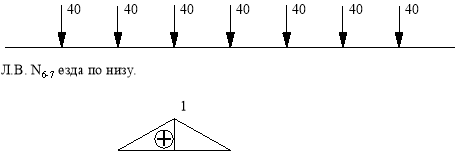
![]()
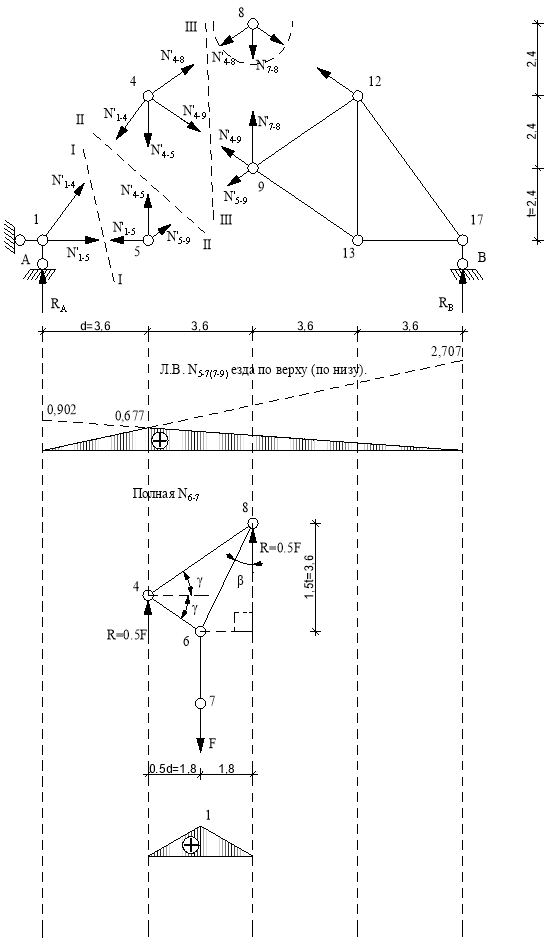 Рис.15
Рис.15
Линия влияния N4-6
Основная ферма.
Используем метод сечений. Рассекаем ферму (сечение III-III) Составим уравнение равновесия относительно оси у.(рис. 16).
Груз справа. Рассматриваем равновесие левой части фермы (рис.16). Составляем уравнение равновесия – сумма проекций всех сил на ось у.
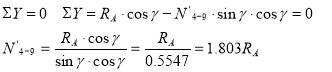
То есть линия влияния ![]() представляет собой линию влияния усилия реакции RA, все ординаты которой умножены на (1,803). Над опорой А откладываем (1,803), соединяем с нулем над опорой В.
представляет собой линию влияния усилия реакции RA, все ординаты которой умножены на (1,803). Над опорой А откладываем (1,803), соединяем с нулем над опорой В.
Получили правую ветвь линии влияния усилия ![]() .
.
Груз слева. Рассматриваем равновесие правой части фермы (рис.16). Составляем уравнение равновесия – сумма проекций всех сил на ось у.
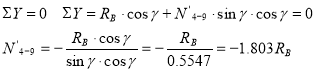
То есть линия влияния ![]() представляет собой линию влияния усилия реакции RB, все ординаты которой умножены на (-1,803). Над опорой В откладываем
представляет собой линию влияния усилия реакции RB, все ординаты которой умножены на (-1,803). Над опорой В откладываем
(-1,803), соединяем с нулем над опорой А.
Получена левая ветвь линии влияния ![]() .
.
Строим передаточную прямую, расположенную под рассеченной панелью. Левый узел 5 рассеченной панели сносим на левую ветвь, правый узел 9 на правую ветвь. Соединяем эти точки и получаем передаточную прямую.
Шпренгель.
Из заданной расчетной схемы (рис.2) выделим шпренгель второй панели
слева (рис.10.1.). Усилие находим методом сечений. Вырезаем узел 7 и рассматриваем его равновесие. Составим уравнение равновесия относительно осей хоу. (рис.10.2.).
Единичная сила в узле 5. ![]()
Единичная сила в узле 9. ![]()
Единичная сила в узле 7.
![]()
![]()
![]()
Геометрически суммируем линии влияния основной и дополнительной ферм
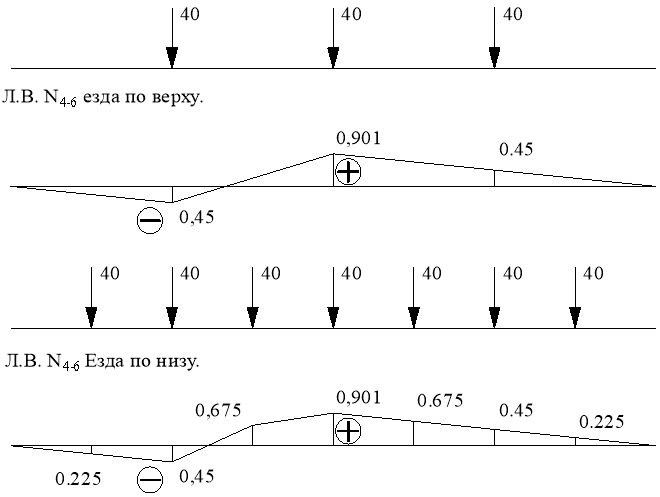
![]()
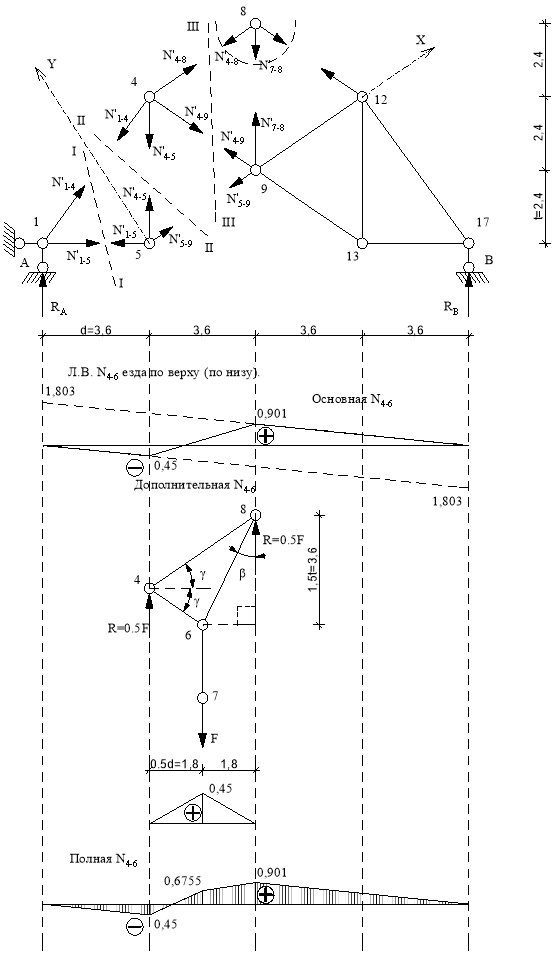 Рис.16
Рис.16
Линия влияния N6-9
Основная ферма.
Используем метод сечений. Рассекаем ферму (сечение III-III) Составим уравнение равновесия относительно оси у.(рис. 17).
Груз справа. Рассматриваем равновесие левой части фермы (рис.17). Составляем уравнение равновесия – сумма проекций всех сил на ось у.
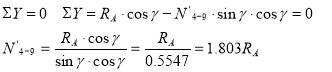
То есть линия влияния ![]() представляет собой линию влияния усилия реакции RA, все ординаты которой умножены на (1,803). Над опорой А откладываем (1,803), соединяем с нулем над опорой В.
представляет собой линию влияния усилия реакции RA, все ординаты которой умножены на (1,803). Над опорой А откладываем (1,803), соединяем с нулем над опорой В.
Получили правую ветвь линии влияния усилия ![]() .
.
Груз слева. Рассматриваем равновесие правой части фермы (рис.17). Составляем уравнение равновесия – сумма проекций всех сил на ось у.
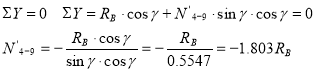
То есть линия влияния ![]() представляет собой линию влияния усилия реакции RB, все ординаты которой умножены на (-1,803). Над опорой В откладываем
представляет собой линию влияния усилия реакции RB, все ординаты которой умножены на (-1,803). Над опорой В откладываем
(-1,803), соединяем с нулем над опорой А.
Получена левая ветвь линии влияния ![]() .
.
Строим передаточную прямую, расположенную под рассеченной панелью. Левый узел 5 рассеченной панели сносим на левую ветвь, правый узел 9 на правую ветвь. Соединяем эти точки и получаем передаточную прямую.
Шпренгель.
Стержень 6-9 принадлежит только основной ферме.
Определение усилия по линиям влияния.
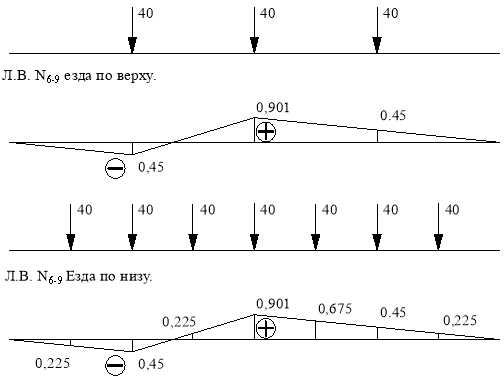
![]()
Линия влияния N6-8 (рис. 17)
Основная ферма.
Стержень 6-8 принадлежит только шпренгелю.
Шпренгель.
Из заданной расчетной схемы (рис.2) выделим шпренгель второй панели
слева (рис.10.1.). Усилие находим методом сечений. Вырезаем узел 7 и рассматриваем его равновесие. Составим уравнение равновесия относительно осей хоу. (рис.10.4.).
Единичная сила в узле 5. ![]()
Единичная сила в узле 9. ![]()
Единичная сила в узле 7.
![]()
Учитывая, что: ![]()
![]()
Определение усилия по линиям влияния.
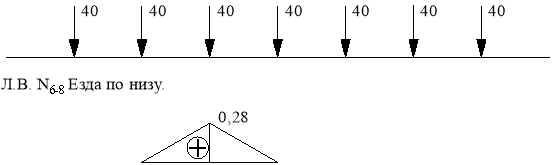
![]()
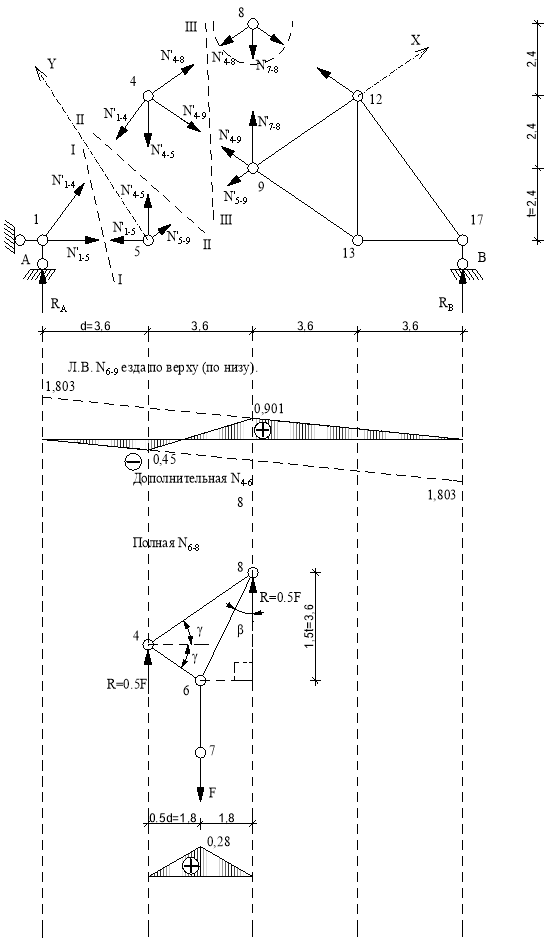 Рис.17
Рис.17
Линия влияния N4-8
Основная ферма.
Используем метод сечений. Рассекаем ферму (сечение III-III) Составим уравнение равновесия относительно моментной точки 9.(рис. 18).
Груз справа. Рассматриваем равновесие левой части фермы (рис.18).
![]()
![]()
То есть линия влияния ![]() представляет собой линию влияния усилия реакции RA, все ординаты которой умножены на (-1,803). Над опорой А откладываем (-1,803), соединяем с нулем над опорой В.
представляет собой линию влияния усилия реакции RA, все ординаты которой умножены на (-1,803). Над опорой А откладываем (-1,803), соединяем с нулем над опорой В.
Получили правую ветвь линии влияния усилия ![]() .
.
Груз слева. Рассматриваем равновесие правой части фермы (рис.18).
![]()
![]()
То есть линия влияния ![]() представляет собой линию влияния усилия реакции RB, все ординаты которой умножены на (-1,803). Над опорой В откладываем
представляет собой линию влияния усилия реакции RB, все ординаты которой умножены на (-1,803). Над опорой В откладываем
(-1,803), соединяем с нулем над опорой А.
Получена левая ветвь линии влияния ![]() .
.
Строим передаточную прямую, расположенную под рассеченной панелью. Левый узел 5 рассеченной панели сносим на левую ветвь, правый узел 9 на правую
ветвь. Соединяем эти точки и получаем передаточную прямую.
Шпренгель.
Из заданной расчетной схемы (рис.2) выделим шпренгель второй панели
слева (рис.10.1.). Усилие находим методом сечений. Вырезаем узел 5 и рассматриваем его равновесие. Составим уравнение равновесия относительно осей хоу. (рис.10.2.).
Единичная сила в узле 5. ![]()
Единичная сила в узле 9. ![]()
Единичная сила в узле 7.
![]()
![]()
![]()
Геометрически суммируем линии влияния основной и дополнительной ферм
Определяем значение усилия по линиям влияния.
![]()
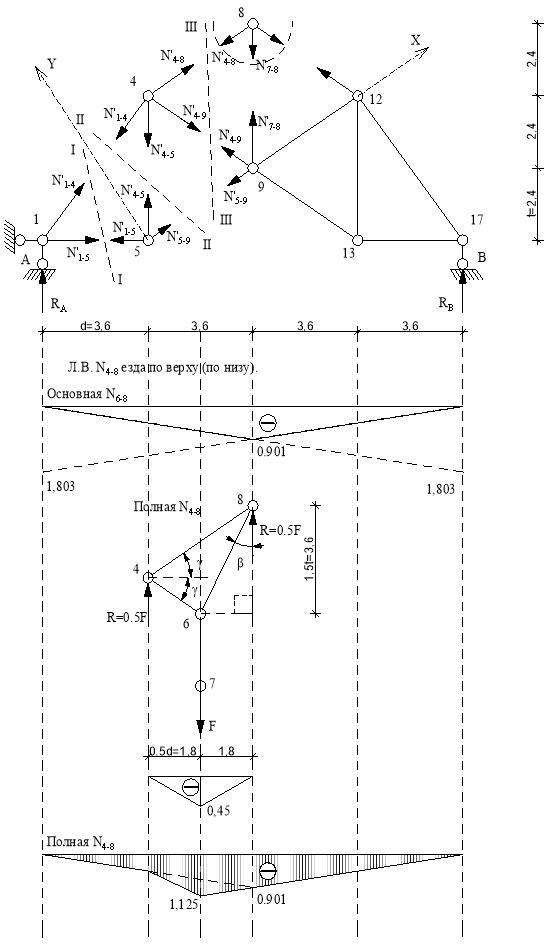 Рис.18
Рис.18
Линия влияния N8-9 (езда по верху)
Основная ферма.
Используем метод сечений. Рассекаем ферму (сечение III-III) Составим уравнение равновесия относительно моментной точки 9.(рис. 19).
Груз слева от узла 8. Рассматриваем равновесие левой части фермы (рис.19).
![]()
![]()
Учитывая что: ![]()
![]()
То есть линия влияния ![]() представляет собой линию влияния усилия реакции RA, все ординаты которой умножены на (2). Над опорой А откладываем
представляет собой линию влияния усилия реакции RA, все ординаты которой умножены на (2). Над опорой А откладываем
(2), соединяем с нулем над опорой В.
Получили правую ветвь линии влияния усилия ![]() .
.
Груз слева. Рассматриваем равновесие правой части фермы (рис.19).
![]()
![]()
Учитывая что: ![]()
![]()
То есть линия влияния ![]() представляет собой линию влияния усилия реакции RB, все ординаты которой умножены на (2). Над опорой В откладываем
представляет собой линию влияния усилия реакции RB, все ординаты которой умножены на (2). Над опорой В откладываем
(2), соединяем с нулем над опорой А.
Получена левая ветвь линии влияния ![]() .
.
Груз в узле 8.
![]()
![]()
Учитывая что: ![]()
![]()
То есть линия влияния ![]() (езда по верху) в точке 8 равна (-1).
(езда по верху) в точке 8 равна (-1).
Шпренгель.
Стержень 8-9 принадлежит только основной ферме.
Линия влияния N8-9 (езда по низу)
Основная ферма.
Используем метод сечений. Рассекаем ферму (сечение III-III) Составим уравнение равновесия относительно моментной точки 9.(рис. 19).
Груз слева от узла 8. Рассматриваем равновесие левой части фермы (рис.19).
![]()
![]()
Учитывая что: ![]()
![]()
То есть линия влияния ![]() представляет собой линию влияния усилия реакции RA, все ординаты которой умножены на (2). Над опорой А откладываем
представляет собой линию влияния усилия реакции RA, все ординаты которой умножены на (2). Над опорой А откладываем
(2), соединяем с нулем над опорой В.
Получили правую ветвь линии влияния усилия ![]() .
.
Груз слева. Рассматриваем равновесие правой части фермы (рис.19).
![]()
![]()
Учитывая что: ![]()
![]()
То есть линия влияния ![]() представляет собой линию влияния усилия реакции RB, все ординаты которой умножены на (2). Над опорой В откладываем
представляет собой линию влияния усилия реакции RB, все ординаты которой умножены на (2). Над опорой В откладываем
(2), соединяем с нулем над опорой А.
Получена левая ветвь линии влияния ![]() .
.
Шпренгель.
Стержень 8-9 принадлежит только основной ферме.
Определение усилия по линиям влияния.
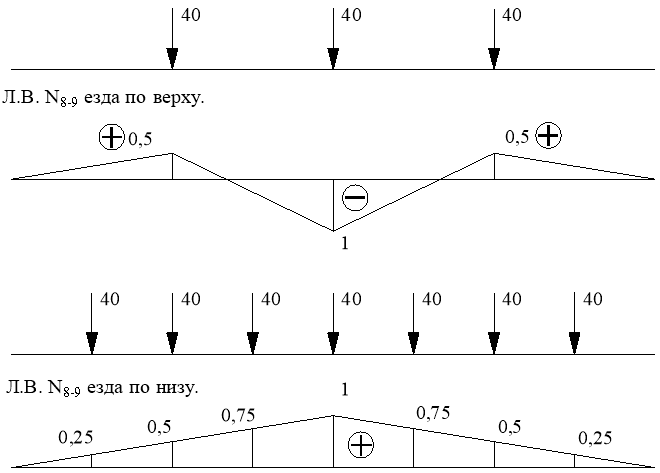
![]()
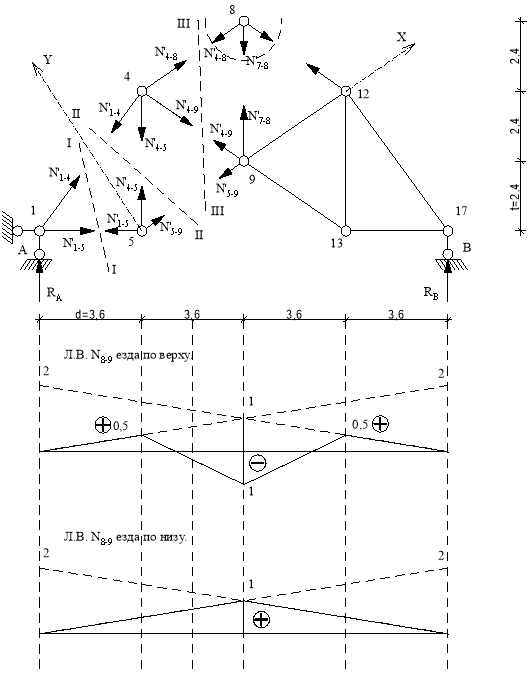
Рис.19
Сравнительная таблица
|
Стержень |
Определение аналитически |
По линиям влияния |
Невязка % |
|
1-3 |
150 |
150 |
0 |
|
3-5 |
150 |
150 |
0 |
|
1-2 |
-250 |
-250 |
0 |
|
2-4 |
-225 |
-225 |
0 |
|
2-3 |
40 |
40 |
0 |
|
2-5 |
-25 |
-25 |
0 |
|
4-5 |
-30 |
-30 |
0 |
|
5-7 |
162,41 |
162,4 |
0,006 |
|
7-9 |
162,41 |
162,4 |
0,006 |
|
4-6 |
126,2 |
126,08 |
0,1 |
|
6-9 |
108,17 |
108,08 |
0,08 |
|
4-8 |
-234,57 |
-234,08 |
0,2 |
|
6-7 |
40 |
40 |
0 |
|
6-8 |
11,18 |
11,2 |
0,18 |
|
8-9 |
160,23 |
160 |
0,14 |
1
Имя файла: ferma.doc
Размер файла: 689 Kb
Если закачивание файла не начнется через 10 сек, кликните по этой ссылке
