Расчет динамических нагрузок при вынужденных колебаниях.

    Требуется определить : 1. Статическое удлинение опорного стержня ;

  2. Статическое перемещение и статическое напряжение сечения балки, где находится электромотор ;

  3. Частоту вынужденных колебаний системы ;

  4. Коэффициент нарастания колебаний в случаях жёсткого опирания балки и упругого опирания ;

  5. Найти закон изменения во времени прогиба балки и максимального нормального напряжения в сечении, где находится электромотор при условии установившихся вынужденных колебаний ;

  6. Построить график этих функций и определить максимальный динамический коэффициент ;

  7. Проверить прочность балки и стержня при допускаемом напряжении [σ]=280 МПа.

                                                                     Решение.

               a=0.35L=0.35×2.6=0.91 м.

    По таблице сортамента определим геометрические характеристики двутавра № 20 :

              Jx=1840 см4 ; Wx=184 см3 ; F=26.8 см2

    1. Найдём статическое удлинение опорного стержня.

    Из уравнений равновесия статики ΣmA=0 и ΣmB=0 найдём опорные реакции в балке AB.

      ΣmA=0  ;  NBL-Qa=0 , откуда  NB=Qa/L=100×0.91/2.6=35 кН

      ΣmB=0 ;  -RAL+Q(L-a)=0 , откуда  RA=Q(L-a)/L=100×(2.6-0.91)/2.6=65 кН

    Найдём вертикальное перемещение опоры B за счёт удлинения подвески при растяжении. Конец балки B переместится (точка B1) на величину :

    YB=NBLs/(EF)  , где F – площадь подвески ; E=2×105 МПа=2×108 кН/м2

    F=πd2/4=3.14×0.0172/4=0.0002 м2

    YB=35×1.4/(2×108×0.0002)=0.0012 м=1.2 мм.

 

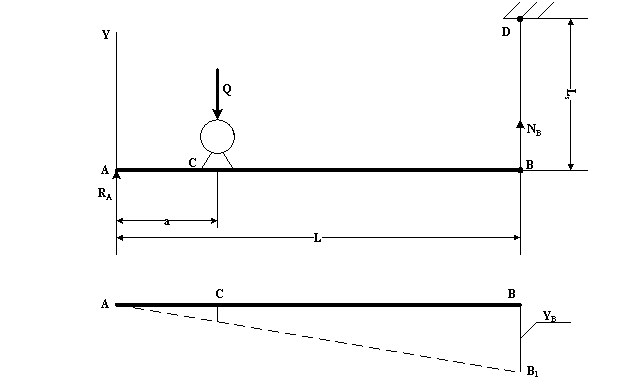
    2. Статическое перемещение и статическое напряжение сечения балки, где находится электромотор.

    Определим статический прогиб в точке «С» балки AB при условии, что опора B является жёсткой.

    Построим эпюру MQ изгибающих моментов от заданной нагрузки.

    Изобразим балку AB , нагруженной единичной силой P=1 в сечении С.

    Находим реакции опор.

              ΣmB=0  ;  -RAL+P(L-a)=0  , откуда  RA=(L-a)/L=(2.6-0.91)/2.6=0.65

              ΣmA=0  ;  RBL-Pa=0  , откуда  RB=a/L=0.91/2.6=0.35

    Строим эпюру изгибающих моментов MP=1 от единичной нагрузки.

               MC=RAa=0.65×0.91=0.59

    Используя правило Верещагина, найдём перемещение в сечении «С»

       YстС==

  =

  =0.004 м=4 мм

    Статическое напряжение в сечении «С» балки.

               σсст=161×106 Па=161 МПа.

    Вычислим величину полного перемещения «С» балки при учёте удлинения подвески по формуле

    Yполн(с) =YстС+YстС(B )=YстС+YстBa/L=0.004+0.0012×0.91/2.6=0.004 м.

 

 

 

 

 

    3. Найдём частоту вынужденных колебаний системы.

    Находим частоту собственных колебаний :

   при жёстком опирании

            ω1=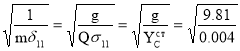=49.5 1/с

  при упругом опирании

            ω2=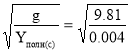=49.5 1/с

    Вертикальная составляющая центробежной силы вызывает поперечные колебания балки в вертикальной плоскости с частотой возмущающей силы.

            Θ=πn/30=3.14×600/30=62.8 1/с.

 

 

    4. Найдём коэффициент нарастания колебаний в случаях жёсткого опирания балки и упругого опирания.

Коэффициент нарастания колебаний при жёстком опирании.

                              β1=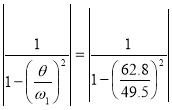=1.6

    Коэффициент нарастания колебаний при упругом опирании.

                          β2=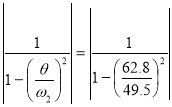=1.6

    5. Найдём закон изменения во времени прогиба балки и максимального нормального напряжения в сечении, где находиться электромотор.

   Находим амплитудное значение инерционной силы :

    P0=Pθ2e/g=×62.82×0.034=25 кН

    Закон изменения во времени прогиба балки в месте, где находится электромотор, при жёстком опирании :

  ν1(t)=νQ1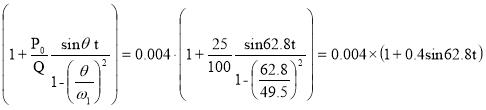  м.

    при упругом опирании

  ν2(t)=νQ2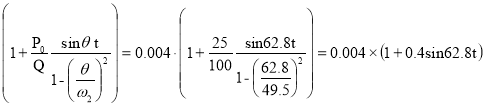 м.

   Период вынужденных колебаний  T=2π/θ=2×3.14/62.8=0.1 c

    Закон изменения во времени максимального напряжения при изгибе балки в сечении С :

    при жёстком опирании :

                   σ1(t)=σQ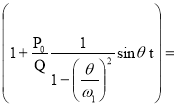

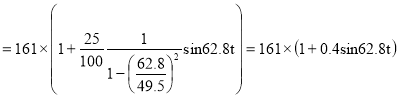             МПа.

    при упругом опирании

                          σ2(t)=161×(1+0.4sin62.8t) МПа.

    6. Построим графики этих функций и определим максимальный динамический коэффициент.

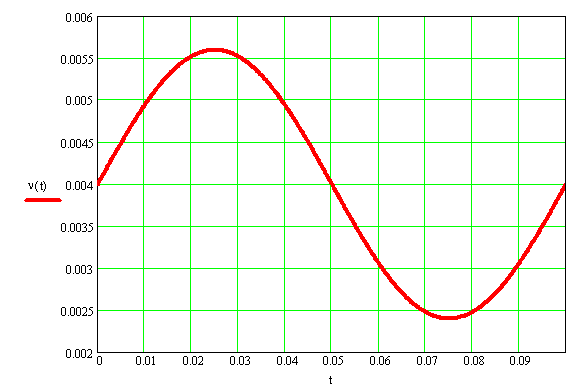
    Для построения графика ν(t) вычисления проводим в табличной форме.

                 ν(t)=0.004×(1+0.4sin62.8t)  м.

t, c	sin62.8t	0.4sin62.8t	ν1, м
0	0	0	0.004
0.025	1	0.4	0.006
0.05	0	0	0.4
0.075	-1	-0.4	0.002
0.1	0	0	0.4

 

 

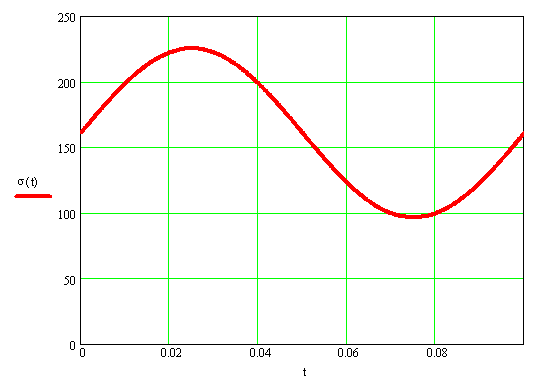
    Для построения графика σ(t) вычисления проводим в табличной форме.

                       σ1(t)= 161×(1+0.4sin62.8t) МПа.

t, c	sin62.8t	0.4sin62.8t	σ(t), МПа
0	0	0	161
0.025	1	0.4	225
0.05	0	0	161
0.075	-1	-0.4	97
0.1	0	0	161

   Коэффициент динамичности

                                  КД=1+P0β/Q=1+25×1.6/100=1.4

    Найдём максимальное напряжение в сечении, где находится электромотор :

                            σmax=σстКД=161×1.4=225 МПа.

    7. Проверим прочность балки и стержня при допускаемом напряжении [σ]=280 МПа.

    Максимальные напряжения в сечении балки : σmax=225 МПа<[σ]=280 МПа.

  Условие прочности соблюдается, причём недонапряжение составляет  20%.

               δ==0.2 

    Максимальное напряжение в сечении стержня :

                σmax=NB/F=35×103/0.0002=175×106 Па=175 МПа<[σ]=280 МПа.

    Условие прочности соблюдается.

    Как видно из расчёта величина прогиба ν и нормальные напряжения σ в сечении балки, где установлен электромотор, оказались одинаковыми, как в случае жёсткого опирания балки, так и в случае упругого опирания балки. Причём при разгоне ротора от нуля до расчётной частоты система проходит момент резонанса (ω<θ ).