Задача №2

 

Для заданных схем нагружения построить эпюры внутренних усилий

а) для Приложения 9 из условия прочности на изгиб по нормальным напряжениям определить размеры поперечного сечения в форме круга, прямоугольника с соотношением сторон h/b= 2 и двутавра. Считать q, а,  известными;

б) для Приложения 10 из условия прочности на изгиб по нормальным напряжениям определить безопасную нагрузку. Поперечное сечение – швеллер № 18. Считать q, а,  известными;

Примечание: в приложении №11 сделать систему один раз статически неопределимую- одну связь убрать на усмотрение обучающегося.

Дано: = 125 Мпа, k= 5, b(m)= 4, c(n)= 3, a= 380 мм, q= 12 Н/мм.

 

Решение

 

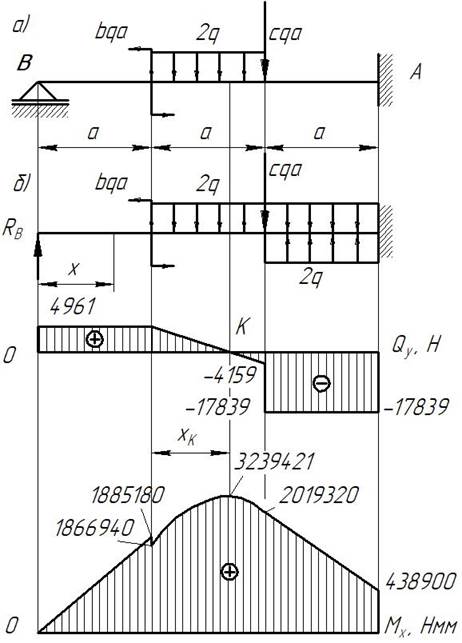
а) Заданная схема один раз статически неопределима, т.к. неизвестных реакций 4, а уравнений статики – 3. Для расчета балки представляем ее как статически определимую, полученную из заданной в результате отбрасывания левой опоры. Балка, показанная на рисунке 2,б, является основной системой для заданной балки 2,а.

На основную систему (рис. 2,б) кроме заданных нагрузок, действует неизвестная реакция R_B.

Для решения задачи используем метод начальных параметров. Составляем уравнения метода начальных параметров для сечения А:

 

; (1)

; (2)

 

            Так как на правом конце балки угол поворота  и прогиб  равны нулю, то из уравнения (1):

 

 

откуда

 

 

 

Из уравнения (2):

 

 

 

 

Так  как прогиб левого конца балки равен нулю, то

 

 

 

            Построим эпюры поперечных сил и изгибающих моментов. Построение начинаем со свободного левого конца.

            При х=0 слева:

Q=0, М=0.

При х=0 справа:

Q= , М=0.

При х=a  слева:  

Q=,

М=.

При х=a справа:

 Q=,

М= -bqa= -4∙12∙380= 1866940 Нмм .

При х=2a  слева:  

Q=,

М= 

При х=2a справа:

Q=,

М= 

При х=3a  слева:  

Q=,

М=

 

 

Эпюр поперечных сил пересекает нулевую линию в точке К. Из уравнения поперечных сил при х=2a справа определяем расстояние х_К.

 

Q= 

,

 

Определяем максимальный изгибающий момент:

 

М_max= 

 

 

 

Из условия прочности на изгиб по нормальным напряжениям:

 

,(3)

 

где - осевой момент сопротивления сечения.

            Из формулы (3):

 

 

            Для сечения в форме круга:

 

 

            Отсюда диаметр круга:

 

           

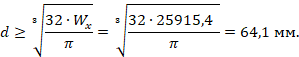
Принимаем d= 65 мм.

Площадь сечения

Для сечения в форме прямоугольника с соотношением сторон h/b= 2:

 

 

где b- ширина прямоугольника,

            h- высота прямоугольника.

            По условию соотношение сторон h/b= 2, отсюда

 

 

 

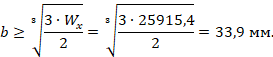
            Принимаем b= 34 мм, тогда h= 2∙34=68 мм.

            Площадь прямоугольника

 

 

 

Для сечения в форме двутавра.

По ГОСТ 8239-89 подвираем двутавр №10 с ,

 

            Сравниваем подобранные профили по площади сечения

 

            Наиболее выгодным является сечение  в форме двутавра.