Пример решения задачи по сопромату - расчет динамической нагрузки(удара)

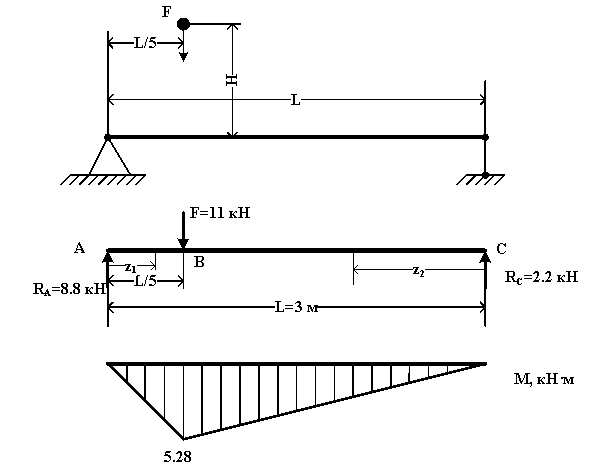
    На двутавровую балку с высоты H падает груз F.

    Требуется :

    1) Определить наибольшие нормальные напряжения в балке ;

    2) Вычислить наибольшие напряжения в балке при условии, что правая опора заменена пружиной, податливость которой (т.е. осадка от груза 1 кН) равна α ;

    3) Сравнить полученные результаты.

    Дано : номер двутавра 36 ; L=3 м ; F=11 кН ; α=3 мм/кН ; H=L/5 (высота падения не задана, поэтому принимаем самостоятельно).

                                                                       Решение.

    Балка подвергается поперечному (изгибающему) удару.

    Условие прочности балки :

                           

    Наибольшее напряжение в балки от статического действия груза :

                            

    где Mx – максимальный момент в сечении балки (определяется по эпюре) ; Wx – момент сопротивления сечения при изгибе, для двутавра № 36 : Wx=743 cм3 (определяется по таблицам сортамента прокатной стали).

    Построим эпюру изгибающих моментов. Определим реакции опор :

              ΣmC=-RAL+0.8FL=0  , откуда

              RA=0.8F=0.8×11=8.8 кН

              ΣmA=RCL-0.2FL=0  , откуда

              RC=0.2F=0.2×11=2.2 кН

    Балка имеет два участка. Обозначим zi расстояние от левого (правого) конца балки до некоторого её сечения. Найдём изгибающие моменты в характерных сечениях балки.

                        MA=0  ; MBл=0.2RAL=0.2×8.8×3=5.28 кН·м ; MBпр=0.8RCL=0.8×2.2×3=5.28 кН·м ; MC=0.

    Эпюра изгибающих моментов построена на рисунке, со стороны растянутых волокон.

    Тогда, при Mx=5.28 кН∙м (в сечении B) наибольшее напряжение в балке от статического действия груза :

                             =7.1×106 Па=7.1 МПа

    Для определения динамического коэффициента вычислим величину прогиба в точке приложения груза от статического действия его.

    Воспользуемся методом начальных параметров. Начало отсчёта абсциссы z примем на опоре A, где y0=0. В точке удара :

                              EJyB=

    Неизвестный начальный параметр ν0 найдём, составив уравнения для сечения С, где yC=0 :

                EJyC=

    Откуда :  ν0= 

    Тогда, при найденном выражении для ν0, получим :

                         EJyB=

                        EJyB=

    Откуда  yB==-9.5×10-5 м=-0.095 мм

    где Е=2×1011 Па – модуль упругости ; J=Jx=13380 см4 – момент инерции (по таблице сортамента прокатной стали).

    Находим динамический коэффициент :

                               kd=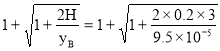=113.4

    Находим динамическое напряжение :

              МПа

    Находим прогиб от динамического действия груза F в точке удара :

               yd=kdyst=kdyB=113.4×0.095=10.8 мм.

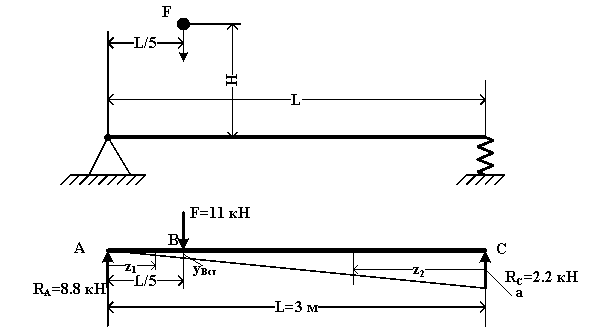
    Вычислим наибольшее напряжение в балке при условии, что правая опора заменена пружиной.

    В случае опирания правого конца балки на пружину при действии на балку статической силы F пружина под влиянием опорной реакции RC=2.2 кН, укоротится на длину a=RCα=

=2.2×3=6.6 мм. Правый конец балки при этом опустится на величину a, а сечение B балки – на величину yBст=0.2a=0.2×6.6=1.32 мм.

    Полное вертикальное перемещение от статического действия силы F в сечении под силой (в сечении B) равно сумме величин прогиба, найденной при расчёте балки без пружины, и перемещения, вызванного сжатием пружины, т.е. :

                                    Δст=yB+yBст=0.095+1.32=1.415 мм.

    Находим динамический коэффициент :

                               kd=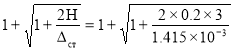=30.1

    Находим динамическое напряжение :

              МПа

    Находим прогиб от динамического действия груза F в точке удара :

               yd=kdyst=kdΔст=30.1×1.415=42.6 мм.

    Таким образом, установка пружины под правым концом балки уменьшила динамические напряжения в 805.14/213.71=3.8 раза.