Пример решения задачи по сопромату - Определение прогиба свободного конца балки переменного сечения.
Ниже приведено условие и решение задачи. Закачка решения в формате doc начнется автоматически через 10 секунд.
Определить прогиб свободного конца балки переменного сечения.
Дано : F=20 кН ; q=8 кН/м ; k=10 ; a=2 м ; b=1.1 м.
Решение.
Определим прогиб свободного конца балки.
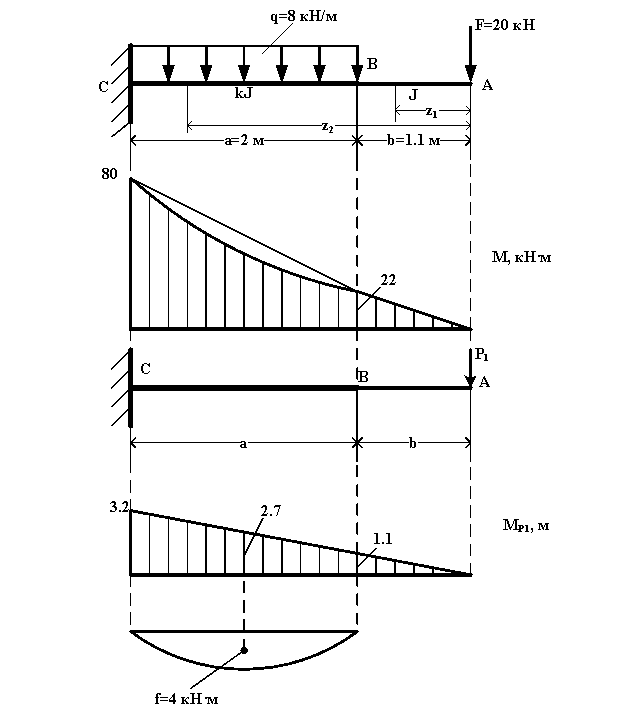
Построим эпюру изгибающих моментов для данного состояния балки. Определим выражения для изгибающих моментов для каждого участка в общем виде. Балка имеет два участка. Обозначим расстояние zi от точки А до некоторого сечения, получим :
На участке AB (ход справа) :
0≤z1≤b ; M1=-Fz1
На участке BC (ход справа) :
b≤z2≤a+b ; M2=-Fz2-0.5q(z2-b)2
Определяем значения изгибающих моментов в характерных точках балки.
Участок AB : при z1=0 ; MA=0 ;
при z1=b ; MBпр=-Fb=-20×1.1=-22 кН·м
Участок BC : при z2=b ; MBл=-Fb=-20×1.1=-22 кН·м ;
при z2=a+b ; MC=-F(a+b)-0.5qa2=-20×(2+1.1)-0.5×8×22=-80 кН·м
На участке AB эпюра ограничена прямой линией, на участке BC эпюра ограничена параболой.
Поперечная сила на участке BC :
![]() <0
<0
Таким образом, на участке BC эпюра не имеет экстремума, так как поперечная сила, на этом участке, не меняет знак.
По полученным данным строим эпюру изгибающих моментов со стороны растянутых волокон.
Рассмотрим балку в состоянии P1 под действием только сосредоточенной силы ![]() , приложенной в точке А.
, приложенной в точке А.
Для построения эпюры МP1 найдём значения изгибающих моментов в характерных сечениях.
MA=0 ; MB=-P1b=-1.1 ; MC=-P1(a+b)=-3.2
По этим данным строим эпюру MP1 со стороны растянутых волокон.
Определим прогиб свободного конца балки Δ1q по формуле Мора с помощью правила Верещагина. При этом криволинейную эпюру Mq на участке BC , можно представить в виде сложения двух эпюр, как показано на рисунке. Стрелка f=qa2/8=8×22/8=4 кН·м. Δ1q=![]() =
=![]()
![]() +
+
+![]() .
.
Знак «плюс» означает, что точка А перемещается вниз (в сторону действия ![]() ).
).
Ответ : Δ1q=![]() .
.
Имя файла: sopr1.doc
Размер файла: 291.5 Kb
Если закачивание файла не начнется через 10 сек, кликните по этой ссылке
