Пример решения задачи на теорию напряженного состояния.

  Требуется:

 1. Определить величину главных напряжений и положение главных площадок;

 2. Найти максимальные касательные напряжения τmax;

 3. Определить относительные деформации и относительное изменение объёма;

4. Установить удельную потенциальную энергию деформации.

                                                                       Решение.

1. Определим величину главных напряжений и положение главных площадок

В соответствии с правилом знаков, устанавливаем : σx=50 МПа ; σy=60 МПа ; τyx=-τxy

 По формуле

   σmax/min=  определим величину главных напряжений.

   σmax==125,2 МПа

   σmin== - 15,2 МПа

Для определения положения главных площадок используем формулу:

   tg2α0=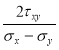== 14 = tg86°

  откуда 2α0=86° и α0=43°

  Для определения площадки, по которой действуют напряжения σmax , поворачиваем горизонтальную площадку (так как по ней действуют нормальные напряжения, больше, чем по вертикальной площадке) на угол α0=43° против часовой стрелки, т.е. в том направлении, в котором вектор касательного напряжения (на поворачиваемой площадке) стремиться вращать элементарный параллелепипед относительно его центра. Найденная площадка показана на рисунке.

 

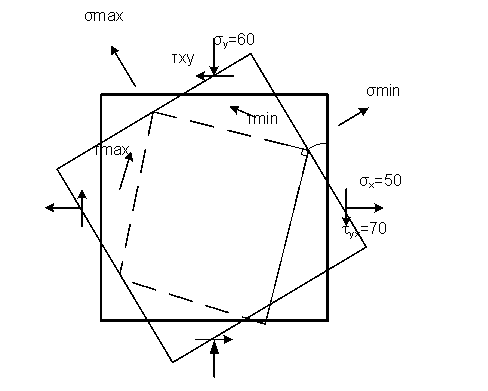
2. Найдём максимальные касательные напряжения τmax

  Максимальные касательные напряжения находим по формуле :

  τmax/min===±140,4 МПа

Положения площадок сдвига (по которым касательные напряжения имеют максимальные значения) определяем по положениям главных площадок, к которым они наклонены под углами 45°. Экстремальные касательные напряжения действуют в направлениях от σmin к σmax.

 

3. Определим относительные деформации и относительное изменение объёма

Относительные деформации находим по формулам:

  εx=(1/E)[σx-μσy]=1/(1.3*1011)[50-0.22*60]*106=2,83*10-4

  εy=(1/E)[σy-μσx]=1/(1.3*1011)[60-0.22*50]*106=3,77*10-4

  Относительное изменение объёма по формуле Ж

  θ=εx+εy=(2,83+3,77)*10-4=6,6*10-4

 

4. Установим удельную потенциальную энергию деформации.

  Удельную потенциальную энергию деформации находим по формуле:

  u== ==57956,7 Дж/м3

Ответ : σmax=125,2 МПа; σmin= -15,2 МПа; τmax/min=±140,4 МПа; εx=2,83*10-4 ; εy=3,77*10-4 ; θ=6,6*10-4 ; u=57956,7 Дж/м3.