Пример решения задач по сопромату(расчет стержня на растяжение и вала на кручение)
Стальной стержень (рис. 1.1) нагружен силами, направленными вдоль его оси. Материал стержня – сталь с модулем продольной упругости E = 2·105 МПа. Построить эпюры продольных сил N, нормальных напряжений и продольных перемещений сечений стержня.
Дано: а=0,2 м; b=0,5 м; c=0,2 м; A1=4 см2; A2=9 см2; F1=40 кН; F2=30 кН; F3=50 кН.
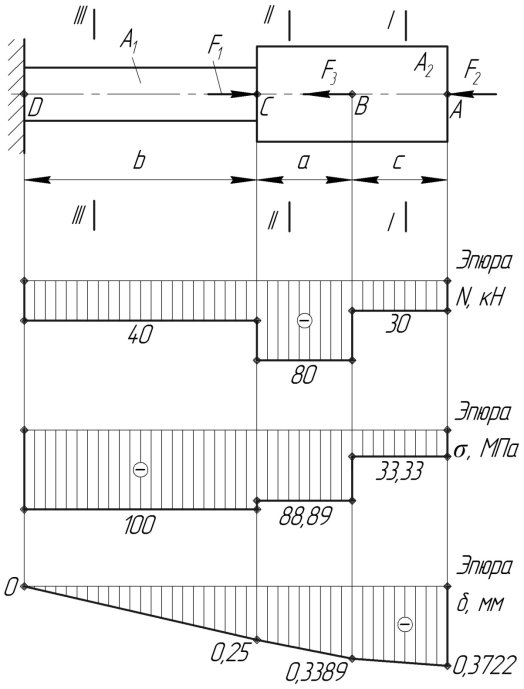
Рис. 1.1. Расчетная схема стержня с эпюрами
Решение
1. Построение эпюры N.
На стержень действуют три силы, следовательно, продольная сила по его длине будет изменяться. Разбиваем стержень на участки, в пределах которых продольная сила будет постоянной. Обозначим сечения буквами А, В, С, D начиная со свободного конца, в данном случае правого.
Для определения продольной силы на каждом участке рассматриваем произвольное поперечное сечение, сила в котором считается положительной при растяжении и отрицательной при сжатии. Ее величина может быть найдена с помощью метода сечений. Чтобы не определять предварительно реакцию в заделке D, начинаем расчеты со свободного конца стержня А.
Участок АВ, сечение I-I. Справа от сечения действует сжимающая сила F2 (рис. 1.1). В соответствии с упомянутым ранее правилом, получаем:
кН.
Участок ВС, сечение II-II. Справа от него расположены две силы, направленные в одну сторону. С учетом правила знаков, получим:
кН.
Участок CD, сечение III-III. Аналогично получаем:
кН.
По найденным значениям N в выбранном масштабе строим эпюру, учитывая, что в пределах каждого участка продольная сила постоянна (рис. 1.1).
Положительные значения N откладываем вверх от оси эпюры, отрицательные - вниз.
2. Построение эпюры напряжений σ.
Вычисляем напряжения в поперечном сечении для каждого участка стержня:
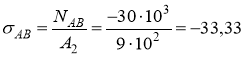МПа;
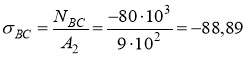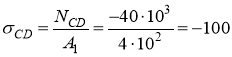МПа;
МПа.
Эпюра напряжений показана на рис. 1.1.
3. Построение эпюры продольных перемещений .
Для построения эпюры перемещений вычисляем абсолютные перемещения отдельных участков стержня, используя закон Гука:
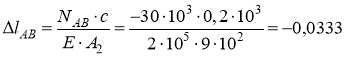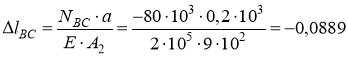мм;
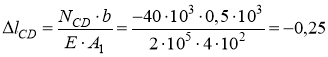мм;
мм.
Определяем перемещения сечений, начиная с неподвижного закрепленного конца. Сечение D расположено в заделке, оно не может смещаться и его перемещение равно нулю: 
.
Сечение С переместится в результате изменения длины участка CD. Перемещение сечения С определяется по формуле:
мм.
Перемещение сечения В является результатом изменения длин CD и ВС. Складывая их перемещения, получаем:
мм.
Рассуждая аналогично, вычисляем перемещение сечения A:
мм.
В выбранном масштабе откладываем от исходной оси значения вычисленных перемещений. Соединив полученные точки прямыми линиями, строим эпюру перемещений (рис. 1.1).
Задача №2
К стальному валу круглого сечения приложены четыре крутящих момента (рис. 2.1). Модуль сдвига стали G=8·104 МПа.
Требуется:
1) построить эпюру крутящих моментов ТК;
2) при заданном значении допускаемого касательного напряжения [τ] определить диаметр вала D из расчета на прочность по наибольшему крутящему моменту и округлить величину D до ближайшего большего значения, оканчивающегося на 0 или 5 мм;
3) построить эпюру углов поворота 
сечений вала относительно заделки.
Дано: а=1 м; b=1,8 м; c=1,2 м; d=1,5 м; Т1=1,7 кН·м; Т2=0,8 кН·м; Т3=1,1 кН·м; Т4=0,6 кН·м; [τ]=50 МПа.
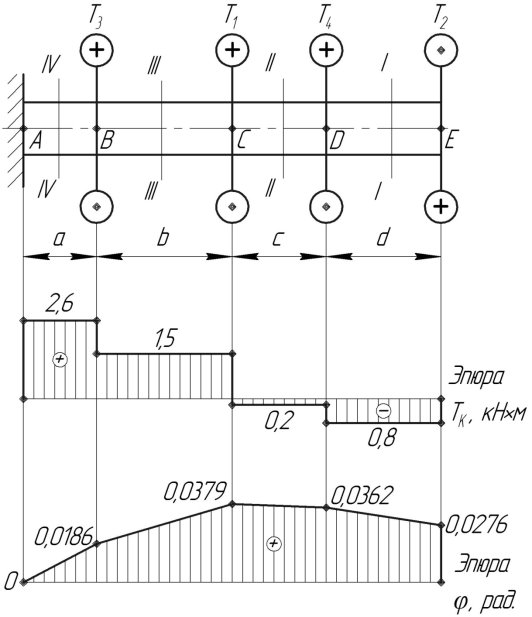
Рис. 2.1. Расчетная схема вала с эпюрами
Решение
1. Построение эпюры крутящих моментов ТК.
Вал жестко заделан левым концом А, правый конец Е свободный. В
сечениях В, С, D и Е приложены крутящие моменты.
Крутящие моменты ТК, определяем методом сечений. Вычисления начинаем с незакрепленного конца:
Участок DE, сечение I-I:
кН·м.
Участок СD, сечение II-II:
кН·м.
Участок ВС, сечение III-III:
кН·м.
Участок АВ, сечение IV-IV:
кН·м.
По найденным значениям ТК строим эпюру крутящих моментов. Для этого рассматриваем последовательно участки DE, CD, BC и AB. Крутящие моменты, действующие на этих участках, уже вычислены.
Величина крутящего момента на каждом участке не зависит от положения сечения в пределах участка (крутящий момент постоянен), поэтому эпюра крутящих моментов ограничена отрезками прямых (рис. 2.1). Построенная эпюра позволяет найти опасное сечение, т.е. такое, в котором действует максимальный (по модулю) крутящий момент.
В данном случае опасными будут сечения в пределах участка АВ. Расчетное значение крутящего момента: 
кН·м.
2. Подбор диаметра поперечного сечения вала D.
Используем условие прочности: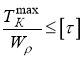 
.
Учитывая, что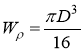 
, выразим диаметр из условия прочности:
,
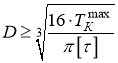отсюда
м = 64 мм, принимаем 
мм.
3. Построение эпюры углов поворота .
Предварительно определим величину полярного момента инерции вала:
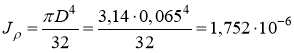м4;
Вычисляем углы закручивания по участкам:
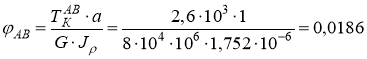рад;
рад;
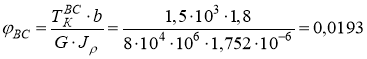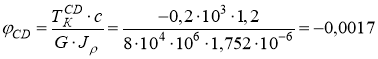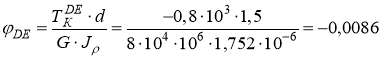рад;
рад.
Угол поворота каждого сечения равен сумме углов закручивания соответствующих участков вала. Суммирование углов начинаем с закрепленного конца А:
, так как сечение в заделке неподвижно;
рад;
рад;
рад;
рад.
По вычисленным углам поворота сечений строим эпюру углов закручивания (рис. 2.1).