Определение усилий в стержнях статически неопределимой системы.

  Дано: F=15 см2; а= 2,5 м; b= 2,6 м; с= 1,7 м.

  Найти:

 1. Найти усилия и напряжения в стержнях, выразив их через силу Q.

2. Найти допускаемую нагрузку Qдоп, приравняв большее из напряжений в двух стержнях к допускаемому напряжению [] = 160 МПа.

3. Найти предельную грузоподъемность системы Qтк и допускаемую нагрузку Qдоп, если предел текучести т = 240 МПа и запас прочности k = 1,5.

4. Сравнить величины Qдоп, полученные при расчете по допускаемым напряжениям и допускаемым нагрузкам.

                                                                            Решение.

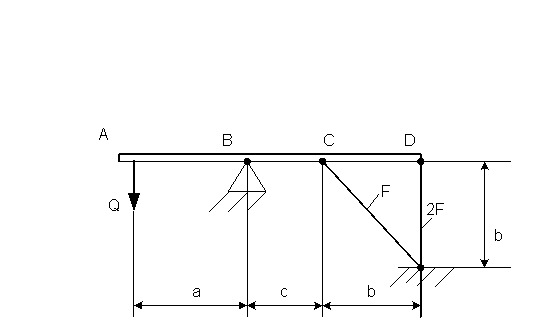
  1. Для составления уравнений равновесия покажем схему сил. Для этого абсолютно жёсткий брус ABCD отсоединим от шарнирно-неподвижной опоры B и прикладываем две реакции Bx и By, стержни 1 и 2 разрезаем и в сечениях показываем продольные силы N1 и N2

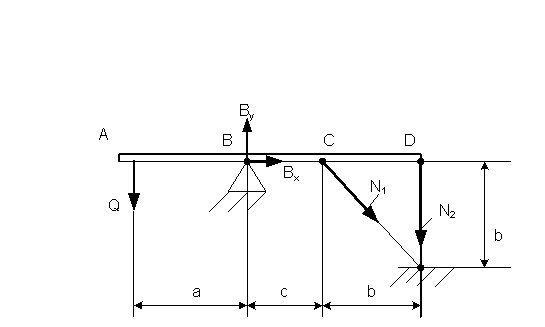
Из трёх уравнений равновесия составим уравнение моментов относительно точки B.

  ∑mB= - c∙N1sin45° + a∙Q – (c+b)∙N2=0

или  - 1,202∙N1 + 2,5Q – 4,3∙N2=0                                          (1)

для составления уравнения совместности деформаций построим схему перемещений. Так как сила Q создаёт момент относительно точки B, то брус ABCD будет поворачиваться против часовой стрелки, вызывая растяжения стержней. Следует иметь ввиду, что деформации стержней ∆l1 и ∆l2 и перемещения δC и δD весьма малы. Вследствие этого дуги окружностей CC1 и DD1, по которым перемещаются шарниры C и D, заменены отрезками касательных.

 

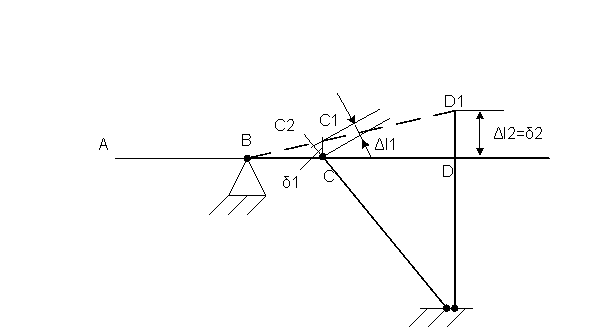
Из прямоугольного треугольника CC1C2 видно, что перемещение δ1 шарнира C из точки C в точку C1 равно : δ1=∆l1/sin45° (∆l1- удлинение стержня 1). Из рисунка видно, что перемеще-   ние шарнира С δ2 равно укорочению ∆l2 второго стержня.

Найдём соотношение ∆l1 и ∆l2. Из подобия треугольников ABB1 и ACC1 следует :

  δ1/δ2=CC1/DD1=BC/BD=c/(c+b)= 1,7/(1,7+2,6)= 0,3953

или ∆l1/(∆l2sin45°)= 0,3953

Окончательно уравнение совместности деформаций примет вид:

  ∆l1=0,2796∙∆l2                                       (2)

Отсюда выражаем N1 через N2

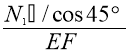  =0.2796∙ 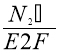, N1=(0.2796∙N2∙cos45°)/2= 0,0989∙N2

Подставив в первое уравнение, получим:

  - 1,202∙N1 + 2,5Q – 4,3∙N2=0 

 1,202∙0,099∙N2 + 4,3∙N2=2,5∙Q

Находим N1 и N2:

  N1=0.056∙Q ;  N2=0,566∙Q

Определяем напряжения 1 и 2 :

  1=N1/F=0.056Q/F=0.056Q/(15*10-4)=37,33Q ; 2=N2/2F=0,566Q/(2∙15∙10-4)=188,67Q

2. Из условия прочности находим Qдоп - допускаемое значение силы.

  max=188,67Q=[] , откуда  Qдоп=[]/188,67=160∙106/188,67=848∙103 Н=848 кН

3. При увеличении нагрузки напряжение в одном стержне достигнет предела текучести ранее, чем в другом. Когда это произойдет напряжение в одном стержне не будет некоторое время расти доже при увеличении нагрузки, система станет как бы статически определимой, нагруженной силой Q и усилием в одном стержне:

N1 = т∙F1            (3)

   При дальнейшем увеличении нагрузки напряжение в другом стержне достигнет предела текучести:

N2 = т∙F2            (3)

   Подставим выражения (3) и (4) в выражение статики (1):

-          1,202∙т∙F + 2,5Q – 4,3∙ т∙2F=0

Откуда находим Qтк:

Qтк = (1,202∙240∙106∙15∙10-4+ 4,3∙240∙106∙2∙15∙10-4) /2,5 = 3528,7 ∙103 Н.

  Находим допустимую нагрузку, разделив предельную грузоподъемность на запас прочности:

Qдоп = 3528,7/1,5 = 2352,5 кН.

4. Сравнивая значения допускаемых нагрузок, полученных в пунктах 2 и 3, рассматриваемой задачи. Можем сделать вывод, значение допускаемой нагрузки, полученной методом допускаемой нагрузке более чем в 2 раза больше значения допустимой нагрузки, полученной методом допускаемых напряжений.