Примеры решения задач по общей теории статистики - контрольная работа 11
Задание 1.
-
Данные группируются по признаку-фактору. Затем по каждой группе рассчитывается среднее значение. Ширина интервала составит:
Для каждого значения ряда подсчитаем, какое количество раз оно попадает в тот или иной интервал. Для этого сортируем ряд по возрастанию.
Х – численность сотрудников, Y – выпуск продукции, млн. р.
|
X |
Интервал |
Количество |
Y |
|
600 |
600 - 900 |
1 |
130 |
|
700 |
600 - 900 |
2 |
140 |
|
750 |
600 - 900 |
3 |
190 |
|
600 - 900 |
4 |
180 |
|
|
820 |
600 - 900 |
5 |
186 |
|
885 |
600 - 900 |
6 |
210 |
|
900 |
900 - 1200 |
1 |
250 |
|
1000 |
900 - 1200 |
2 |
260 |
|
1150 |
900 - 1200 |
3 |
280 |
|
1200 |
1200 - 1500 |
1 |
370 |
|
1200 |
1200 - 1500 |
2 |
340 |
|
1205 |
1200 - 1500 |
3 |
310 |
|
1280 |
1200 - 1500 |
4 |
420 |
|
1280 |
1200 - 1500 |
5 |
370 |
|
1290 |
1200 - 1500 |
6 |
370 |
|
1340 |
1200 - 1500 |
7 |
570 |
|
1350 |
1200 - 1500 |
8 |
462 |
|
1400 |
1200 - 1500 |
9 |
580 |
|
1400 |
1200 - 1500 |
10 |
580 |
|
1400 |
1200 - 1500 |
11 |
580 |
|
1410 |
1200 - 1500 |
12 |
480 |
|
1500 |
1200 - 1500 |
13 |
605 |
Аналитическая группировка.
|
Группы |
Кол-во предприятий, nj |
Общая численность сотрудников |
Xcp , средняя численность сотрудников на одно предприятие |
Общий выпуск продукции, млн. р. |
Ycp, выпуск продукции на одно предприятие, млн. р. |
|
600 - 900 |
6 |
4555 |
759.17 |
1036 |
172.67 |
|
900 - 1200 |
3 |
3050 |
1016.67 |
790 |
263.33 |
|
1200 - 1500 |
13 |
17255 |
1327.31 |
6037 |
464.38 |
|
Итого |
22 |
24860 |
7863 |
Вывод: с возрастанием численности сотрудников возрастает объём выпуска продукции на предприятиях.
-
Данные группируются по признаку-фактору. Затем по каждой группе рассчитывается среднее значение.
Х – стоимость основных фондов, млн. р., Y – выпуск продукции, млн. р.
Ширина интервала составит:
Для каждого значения ряда подсчитаем, какое количество раз оно попадает в тот или иной интервал. Для этого сортируем ряд по возрастанию.
|
X |
Интервал |
Количество |
Y |
|
6 |
6 - 12 |
1 |
190 |
|
7 |
6 - 12 |
2 |
140 |
|
8 |
6 - 12 |
3 |
130 |
|
8 |
6 - 12 |
4 |
180 |
|
9 |
6 - 12 |
5 |
186 |
|
11 |
6 - 12 |
6 |
260 |
|
11 |
6 - 12 |
7 |
210 |
|
12 |
12 - 18 |
1 |
250 |
|
12 |
12 - 18 |
2 |
280 |
|
13 |
12 - 18 |
3 |
310 |
|
14 |
12 - 18 |
4 |
370 |
|
15 |
12 - 18 |
5 |
340 |
|
15 |
12 - 18 |
6 |
370 |
|
16 |
12 - 18 |
7 |
370 |
|
17 |
12 - 18 |
8 |
420 |
|
18 |
18 - 24 |
1 |
462 |
|
18 |
18 - 24 |
2 |
580 |
|
19 |
18 - 24 |
3 |
480 |
|
19 |
18 - 24 |
4 |
570 |
|
21 |
18 - 24 |
5 |
580 |
|
21 |
18 - 24 |
6 |
580 |
|
24 |
18 - 24 |
7 |
605 |
Аналитическая группировка.
|
Группы |
Кол-во предприятий, nj |
Суммарная стоимость основных фондов, млн. р. |
Xcp Стоимость основных фондов на одно предприятие, млн. р. |
Общий выпуск продукции, млн. р. |
Ycp, выпуск продукции на одно предприятие, млн. р. |
|
6 - 12 |
7 |
60 |
8.57 |
1296 |
185.14 |
|
12 - 18 |
8 |
114 |
14.25 |
2710 |
338.75 |
|
18 - 24 |
7 |
140 |
20 |
3857 |
551 |
|
Итого |
22 |
314 |
7863 |
Вывод: с возрастанием стоимости основных средств возрастает объём выпуска продукции на предприятиях.
Задание 2
Задача 1
Строим комбинированную аналитическую группировку.
|
№ |
Уровень образования |
Стаж работы, лет |
Заработная плата за месяц, руб. |
|
2 |
Среднее |
2 |
4800 |
|
3 |
Среднее |
4 |
10100 |
|
16 |
Среднее |
5 |
5300 |
|
5 |
Среднее |
6 |
5700 |
|
10 |
Среднее |
7 |
10100 |
|
8 |
Среднее |
12 |
12800 |
|
13 |
Среднее |
13 |
13100 |
|
9 |
Среднее специальное |
5 |
9300 |
|
4 |
Среднее специальное |
7 |
9800 |
|
12 |
Среднее специальное |
8 |
9150 |
|
6 |
Среднее специальное |
9 |
7960 |
|
1 |
Среднее специальное |
10 |
12050 |
|
14 |
Среднее специальное |
11 |
13700 |
|
11 |
Среднее специальное |
12 |
13900 |
|
15 |
Среднее специальное |
13 |
14000 |
|
7 |
Среднее специальное |
15 |
14300 |
Группировка по фонду заработной платы:
|
Стаж работы |
До 10 лет |
Более 10 лет |
|
Образование |
||
|
Среднее |
36000 |
25900 |
|
Среднее специальное |
36210 |
67950 |
Группировка по средней заработной плате:
|
Стаж работы |
До 10 лет |
Более 10 лет |
|
Образование |
||
|
Среднее |
7200 |
12950 |
|
Среднее специальное |
9052,5 |
13590 |
Видим, что с увеличением стажа и уровня образования заработная плата возрастает.
Задача 2
Составим таблицу.
|
Начало года |
2002 |
2003 |
2004 |
2005 |
2006 |
|
Зарегистрировано кредитных организаций, всего |
2003 |
1828 |
1668 |
1518 |
1409 |
|
из них действующих |
1319 |
1329 |
1329 |
1011 |
1009 |
|
Число филиалов действующих кредитных организаций |
3433 |
3326 |
|
|
|
|
Из них филиалы сбербанка |
1233 |
1162 |
1045 |
|
|
|
Число кредитных организаций с иностранным участием |
130 |
125 |
126 |
131 |
136 |
Задание 3
Задача 1
Построим дискретный вариационный ряд. Для этого отсортируем ряд по возрастанию и подсчитаем количество повторения для каждого элемента ряда.
|
xi |
Кол-во, fi |
Относительная частота, fi/f |
|
2 |
4 |
0.133 |
|
3 |
8 |
0.267 |
|
4 |
11 |
0.367 |
|
5 |
7 |
0.233 |
|
Итого |
30 |
1 |
Изобразим ряд графически.
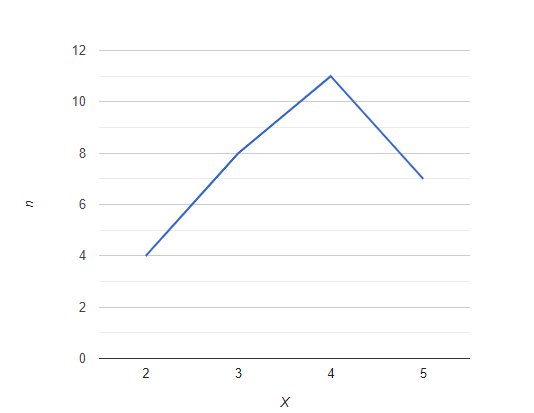
Разобьём рад на успевающих и не успевающих.
|
xi |
Кол-во, fi |
|
Неуспевающие |
4 |
|
Успевающие |
26 |
|
Итого |
30 |
Задача 2
Ширина интервала составит:
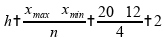
xmax - максимальное значение группировочного признака в совокупности.
xmin - минимальное значение группировочного признака.
Определим границы группы.
|
Номер группы |
Нижняя граница |
Верхняя граница |
|
1 |
12 |
14 |
|
2 |
14 |
16 |
|
3 |
16 |
18 |
|
4 |
18 |
20 |
Одно и тоже значение признака служит верхней и нижней границами двух смежных (предыдущей и последующей) групп.
Для каждого значения ряда подсчитаем, какое количество раз оно попадает в тот или иной интервал. Для этого сортируем ряд по возрастанию.
|
12 |
12 − 14 |
1 |
|
12 |
12 − 14 |
2 |
|
12 |
12 − 14 |
3 |
|
12 |
12 − 14 |
4 |
|
13 |
12 − 14 |
5 |
|
13 |
12 − 14 |
6 |
|
14 |
14 − 16 |
1 |
|
14 |
14 − 16 |
2 |
|
14 |
14 − 16 |
3 |
|
14 |
14 − 16 |
4 |
|
15 |
14 − 16 |
5 |
|
15 |
14 − 16 |
6 |
|
15 |
14 − 16 |
7 |
|
16 |
16 − 18 |
1 |
|
16 |
16 − 18 |
2 |
|
16 |
16 − 18 |
3 |
|
16 |
16 − 18 |
4 |
|
16 |
16 − 18 |
5 |
|
17 |
16 − 18 |
6 |
|
17 |
16 − 18 |
7 |
|
17 |
16 − 18 |
8 |
|
17 |
16 − 18 |
9 |
|
17 |
16 − 18 |
10 |
|
18 |
18 − 20 |
1 |
|
18 |
18 − 20 |
2 |
|
18 |
18 − 20 |
3 |
|
18 |
18 − 20 |
4 |
|
18 |
18 − 20 |
5 |
|
19 |
18 − 20 |
6 |
|
19 |
18 − 20 |
7 |
|
19 |
18 − 20 |
8 |
|
19 |
18 − 20 |
9 |
|
20 |
18 − 20 |
10 |
|
20 |
18 − 20 |
11 |
|
20 |
18 − 20 |
12 |
|
20 |
18 − 20 |
13 |
Результаты группировки оформим в виде таблицы:
|
Группы |
№ совокупности |
Частота fi |
|
12 − 14 |
1,12,19,32,10,36 |
6 |
|
14 − 16 |
23,24,27,30,13,28,33 |
7 |
|
16 − 18 |
3,18,21,29,34,5,8,9,11,25 |
10 |
|
18 − 20 |
2,15,17,20,22,6,16,26,31,4,7,14,35 |
13 |
Изобразим ряд графически.
Построим ряд, поступивших и не поступивших.
|
xi |
Кол-во, fi |
|
Непоступившие |
10 |
|
Поступившие |
26 |
|
Итого |
36 |
Задача 3
Построим ряд динамики валового сбора культур в регионе.
|
Годы |
Валовой сбор, млн. тонн |
|
2000 |
237 |
|
2001 |
179 |
|
2002 |
189 |
|
2003 |
158 |
|
2004 |
186 |
|
2005 |
192 |
|
2006 |
172 |
|
2007 |
191 |
|
2008 |
210 |
|
2009 |
211 |
