Пример самостоятельной работы по статистике

<

Самостоятельная работа №4

N = 2.

Задание 1. Известны следующие данные по организациям региона:

Рассчитайте: 1) коэффициент корреляции знаков Фехнера; 2) коэффициент линейной парной корреляции между признаками. Сделайте выводы о силе, направлении и форме зависимости между двумя признаками;

Определите: 3) параметры уравнения регрессионной зависимости прибыли организаций от объема основных фондов и представьте полученную зависимость аналитически и графически; 4) теоретические значения результативного признака по уравнению регрессии; 5) значение эмпирического корреляционного отношения; 6) оцените значимость полученного уравнения регрессии с помощью дисперсионного критерия Фишера для уровня значимости α=0,05 и сделайте выводы о аналитических возможностях полученной регрессионной модели.

Решение

Примем за зависимую переменную Y - прибыль, за факторную Х - стоимость основных фондов.

1. Рассчитаем коэффициент корреляции знаков Фехнера промежуточные расчёты представим в таблице ниже.

Из таблицы  которая приведена ниже, видно, что число пар, у которых знаки отклонений не совпали , таким образом, число пар, у которых знаки отклонений совпали .

 

Тогда:

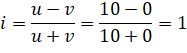
2) Для вычисления коэффициента линейной корреляции проведем в таблице промежуточные расчёты.

 

Коэффициент корреляции найдем по формуле:

 

 

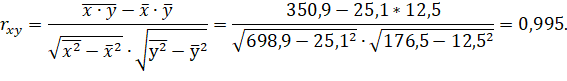
Выводы:

Линейный коэффициент корреляции положителен и близок к 1, следовательно, связь между результативным и факторным признаками очень сильная прямая.

Коэффициент корреляции Фехнера положительный и равен 1, т.е. подтверждается очень сильная прямая связь между стоимостью основных фондов и прибылью.

3) Найдем параметры уравнения регрессии  зависимости прибыли организаций от объема основных фондов.

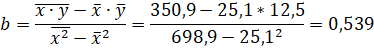
Получено уравнение регрессии:

Таким образом, увеличение стоимости основных фондов на 1 млн. руб. приведет к увеличению прибыли на 0,539 млн. руб.

Представим полученную зависимость аналитически и графически:

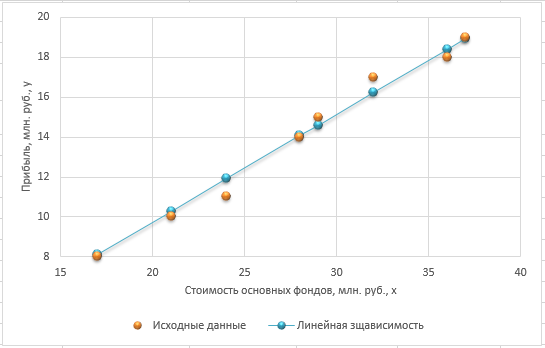
 4) теоретические значения результативного найдем, подставляя в полученное уравнения значения Х.  Результаты расчётов представлены в расчетной таблице под наименованием ŷ.

5) значение эмпирического корреляционного отношения найдем по формуле:

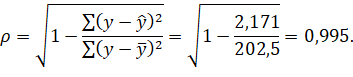
6) оценим значимость полученного уравнения регрессии с помощью дисперсионного критерия Фишера для уровня значимости α=0,05.

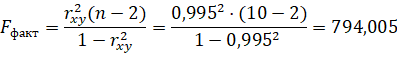
Табличное значение критерия при пятипроцентном уровне значимости и степенях свободы k₁ = 1 и k₂= 10-2= 8 составляет F_табл= 5,32.

Вывод: так как F_факт>F_табл, то уравнение регрессии в целом признается статистически значимым, т.е. стоимость основных фондов оказывает значимое влияние на прибыль.

 

Задание 2. В результате обследования организаций получены следующие данные:

Показатель	Коэффициент износа основных фондов, %
	До 10	10-20	20-30	30-40	40-50	50-60	60 и более
Число предприятий	10	11	15	20	30	8	6
Производительность труда, тыс. шт. в год	8,5	10	7,9	7,9	6,5	6	5,8

1) Рассчитайте показатели степени тесноты корреляционной парной зависимости: коэффициент парной линейной корреляции; коэффициент ранговой корреляции Спирмена. Сделайте вывод о силе корреляционной зависимости, ее направлении и форме связи между признаками.

2) Определите параметры уравнения линейной регрессии. Дайте экономическую интерпретацию параметров уравнения. По уравнению регрессии исчислите теоретическое значения результативного признака по каждой группе организаций.

3) Проверьте полученное уравнение линейной регрессии на значимость для α=0,05.

Решение

Примем за зависимую переменную Y - производительность труда, за факторную Х - коэффициент износа основных фондов (т.к. даны интервальные данные за Х примем ледерины интервалов.

1. Коэффициент парной линейной корреляции найдем по формуле:

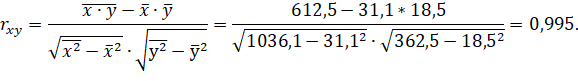
Для сгруппированных данных все средние будем рассчитывать по формуле средней арифметической взвешенной:

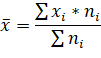
Результаты расчетов представим в таблице:

Показатель	Коэффициент износа основных фондов, %, х							Сумма	Среднее
	5	15	25	35	45	55	65	-	-
Число предприятий	10	11	15	20	30	8	6	100	-
Производительность труда, тыс. шт. в год, у	8,5	10	7,9	7,9	6,5	6	5,8	-	-
xn	50	165	375	700	1350	440	390	3470	34,7
yn	85	110	118,5	158	195	48	34,8	749,3	7,493
xyn	425	1650	2962,5	5530	8775	2640	2262	24244,5	242,445
nx2	250	2475	9375	24500	60750	24200	25350	146900	1469
ny2	722,5	1100	936,15	1248,2	1267,5	288	201,84	5764,19	57,642

Тогда:

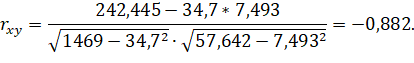
Рассчитаем коэффициент корреляции рангов Спирмена:

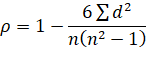
Ранжирование значений показателей приведем в таблице:

№ пред.	х	у	Ранги по х,	Ранги по y,
1	5	8,5	1	6	25
2	15	10	2	7	25
3	25	7,9	3	4,5	2,25
4	35	7,9	4	4,5	0,25
5	45	6,5	5	3	4
6	55	6	6	2	16
7	65	5,8	7	1	36
Сумма					108,5

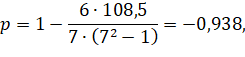
Выводы:

Линейный коэффициент корреляции отрицательный и находится в интервале от 0,7 до 0,9, следовательно, связь между результативным и факторным признаками сильная обратная.

Коэффициент корреляции Спирмена отрицательный и близок к 1, т.е. подтверждается очень сильная обратная связь между износом основных фондов и производительностью труда.

2) Найдем параметры уравнения регрессии  зависимости прибыли организаций от объема основных фондов.

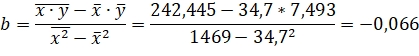
Получено уравнение регрессии:

Экономическая интерпретация: с увеличением коэффициента износа основных фондов на 1 производительность труда снизится на 0,066 тыс. шт. в год.

По уравнению регрессии исчислим теоретическое значения результативного признака по каждой группе организаций. результаты представим в таблице:

 

 

 

3) Проверим полученное уравнение линейной регрессии на значимость для α=0,05.

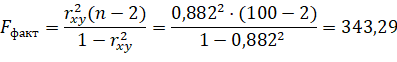
Табличное значение критерия при пятипроцентном уровне значимости и степенях свободы k₁ = 1 и k₂= 100-2= 98 составляет F_табл= 3,94.

Вывод: так как F_факт>F_табл, то уравнение регрессии в целом признается статистически значимым, т.е. износ основных фондов оказывает значимое влияние на производительность труда.