Теория функций комплексного переменного.

№1 Найдите изображения данных оригиналов и укажите, какими теоремами пользовались.

1)

Решение.

Преобразуем данный оригинал по формуле

Находим изображение по формуле 

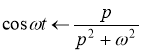
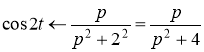
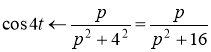
То по свойству линейности изображений следует, что

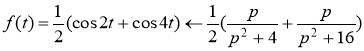
Ответ: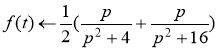

2)

Находим изображение и по формулам 

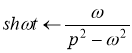
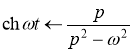
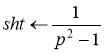
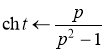
По теореме смещения . Тогда

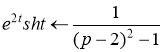
По свойству линейности окончательно получаем

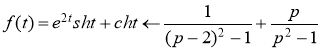
Ответ: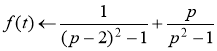

 

3)

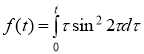
По формуле понижения степени упростим

Тогда

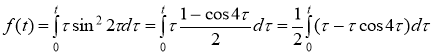
Находим изображение и по формулам 

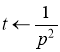
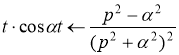
Находим

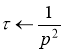
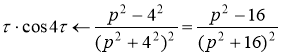
С учетом свойства линейности

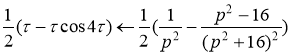
По теореме интегрирования изображений, получаем

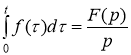
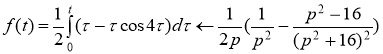
Ответ: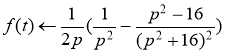

4)

По формуле 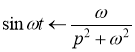получаем

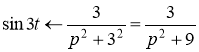
По свойству линейности

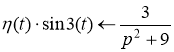
По теореме запаздывания

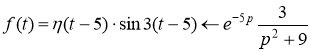
Ответ: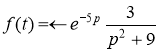

 

5)

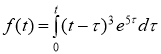
Данный интеграл есть свертка оригиналов и .

Операции свертки оригиналов соответствует умножение изображений.

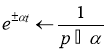Так как и , то

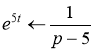
То по  теореме об умножении изображений.

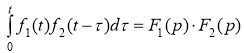, получаем

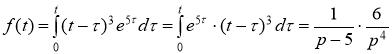
Ответ: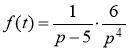

6)

 

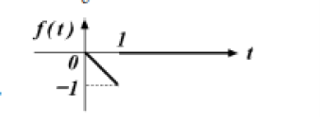
Аналитическая запись функции имеет вид

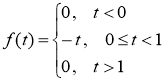
Применяя функцию Хевисайда, данную функцию можно представить следующим образом.

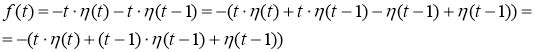
Так как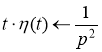

На основании теоремы запаздывания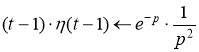

По свойству линейности получим

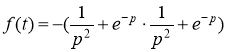
Ответ: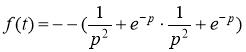

 

7)

Разложим функцию по степеням t-5 пользуясь формулой Тейлора

, =5

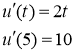
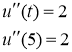
Тогда

Получаем

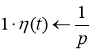
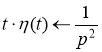
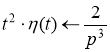
Согласно теореме запаздывания

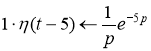
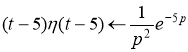
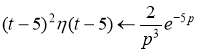
Применим свойство линейности

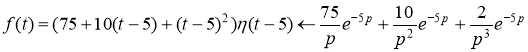
Ответ: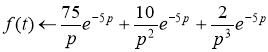

 

 

 

 

 

 

 

 

№8 Найдите оригинал изображения 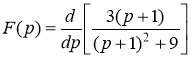с помощью свойств преобразования Лапласа.

Решение.

 Наличие слагаемого в сумме , стоящей в знаменателе, говорит о том, что косинус имеет смещение, т.е. нужно воспользоваться формулой

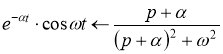
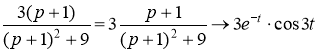
По теореме о дифференцировании изображения, имеем

 

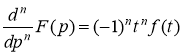
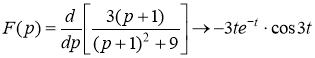
Ответ:

 

№9 Найдите оригинал изображения 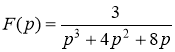с помощью вычетов.

Решение.

Для отыскания f(t) нужно найти сумму вычетов функции во всех особых точках . Найдем корни знаменателя

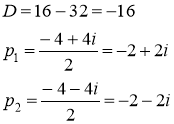
Получили корни . Все корни являются простыми полюсами для функции . Для простого полюса справедливо следующее: если 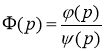, а р0 является простым полюсом , то вычет можно вычислить по формуле

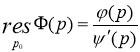
В данном случае , ,

Следовательно

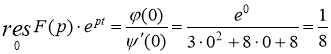
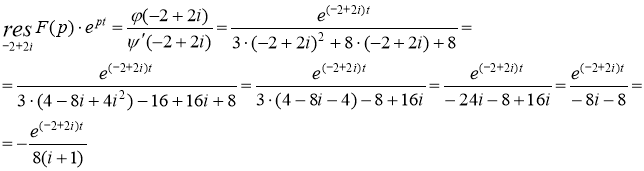
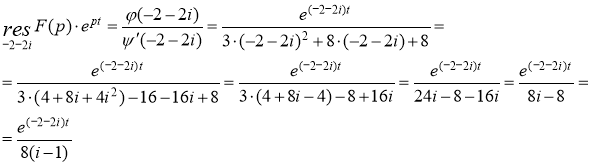
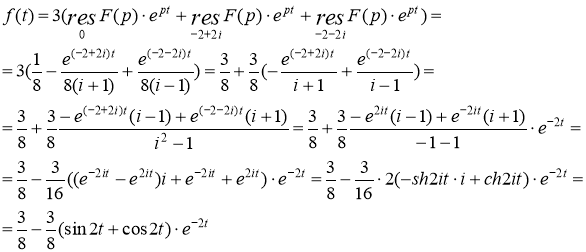
Были учтены формулы:

,

,

Ответ:

 

№10 Найдите оригинал изображения 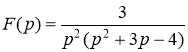с помощью разложения рациональной дроби в сумму элементарных.

Решение.

Найдем корни знаменателя функции

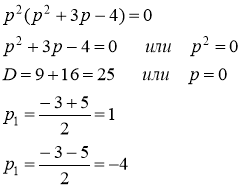
Разложим данную дробь на элементарные

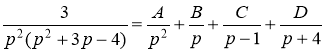
Приведя правую часть последнего равенства к общему знаменателю и приравняв числители дробей, получим тождество:

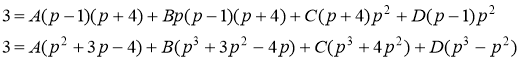
Найдём искомые коэффициенты из системы:

 

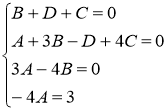
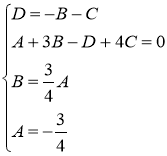
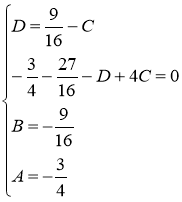
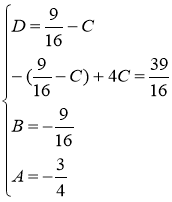
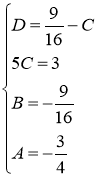
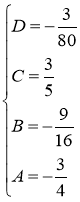
Тогда

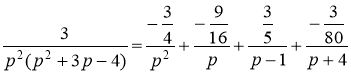
Применяя теорему смещения и свойство линейности, получим

, ,

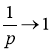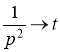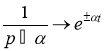
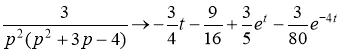
Ответ: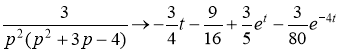

 

№11 Решить дифференциальное уравнение с заданными начальными условиями

,

Решение.

Запишем уравнение в изображениях

Пусть , то

 ,

С учетом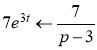

исходное дифференциальное уравнение запишется в виде

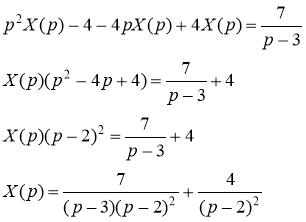
Разложим дробь 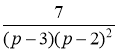на простые дроби

 

 

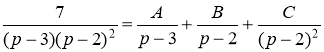
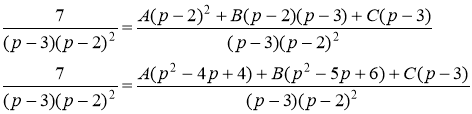
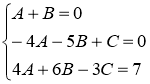
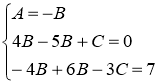
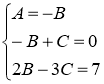
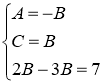
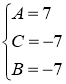
Тогда

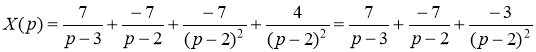
Используя соответствия

   

, ,

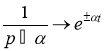
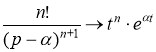
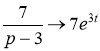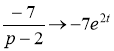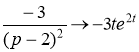
получаем искомое частное решение дифференциального уравнения:

Ответ:

 

 

 

 

 

 

№12 Решить дифференциальное уравнение с заданными начальными условиями

,

Решение.

Запишем уравнение в изображениях

Пусть , то

 ,

С учетом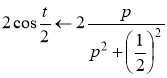

исходное дифференциальное уравнение запишется в виде

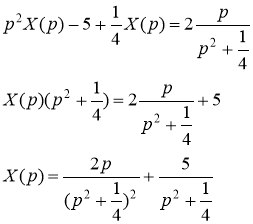
Используя соответствия

  

 

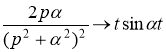
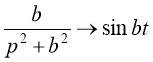
Получим

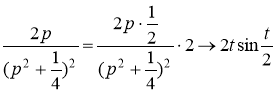
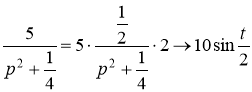
получаем искомое частное решение дифференциального уравнения:

Ответ: