Ряды.

№1 Исследовать на сходимость ряды

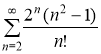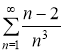а) , б) , в)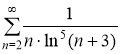

г) Исследовать на сходимость и абсолютную сходимость

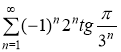
Решение.

а)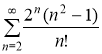

Воспользуемся признаком Даламбера

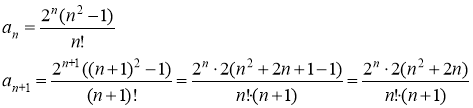
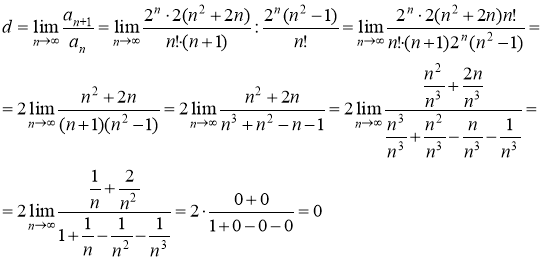
Так как то ряд  сходится.

 

б)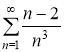

Воспользуемся предельным признаком сравнения. Будем сравнивать заданный ряд со сходящимся обобщенным гармоническим рядом . Тогда

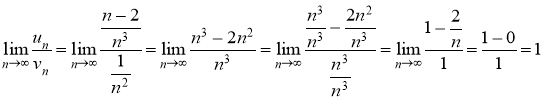
Следовательно, данный ряд сходится в соответствии с предельным признаком сравнения. 

 

в)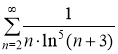

Сравним данный ряд 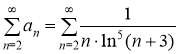с рядом .

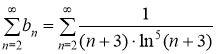Исследуем на сходимость ряд 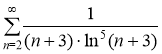с помощью интегрального признака сравнения.

 Рассмотрим функцию

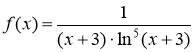
Так как

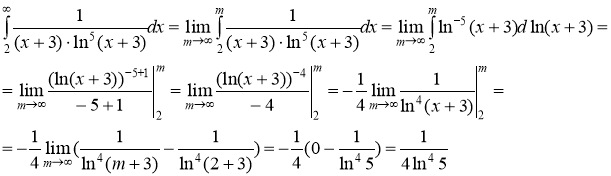
Тогда ряд 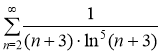сходится вместе с несобственным интегралом.

Так как 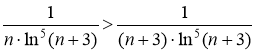, откуда по признаку сравнения в конечной форме следует сходимость ряда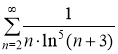

 

г) Исследовать на сходимость и абсолютную сходимость

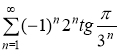
Исследуем на сходимость данный ряд. Для этого составим ряд из абсолютных величин его членов, то есть вида

 

Исследуем сходимость ряда по признаку Даламбера. Находим

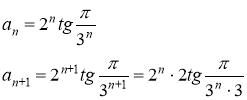
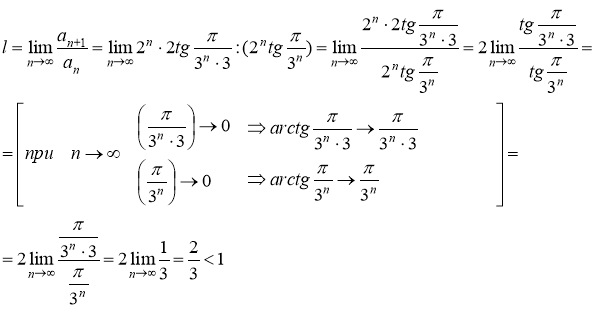
то данный ряд по признаку Даламбера сходится, а исходный ряд сходится абсолютно.

Ответ: а) сходится по признаку Даламбера, б) сходится по предельному признаку, в) сходится по признаку сравнения в конечной форме, г) сходится абсолютно.

 

 

№2 Найти область сходимости ряда

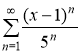
Решение.

Интервал сходимости находим из следующего условия:

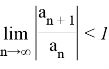
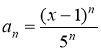
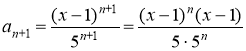
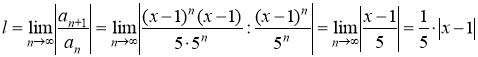
Следовательно, ряд сходится при

  .

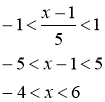Исследуем сходимость ряда на концах этого интервала.

При х =   имеем ряд

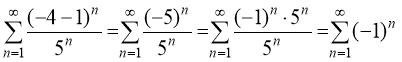
Это знакочередующийся ряд, он расходится, так как для него не  выполняются условия признака Лейбница: общий член ряда не стремится к нулю:

При х =6  имеем ряд

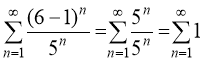
Данный ряд расходится, т.к. не выполнено необходимое условие сходимости рядов: общий член ряда не стремится к нулю .

Следовательно, областью сходимости исходного ряда является интервал .

Ответ: