Примеры решенных задач по математике - Контрольная 4
Ниже приведены условия и решения задач. Закачка решений в формате doc начнется автоматически через 10 секунд.
Задание 1.
Вычислить пределы:
9 а) ![]() ;
;
б) ![]() ;
;
в) 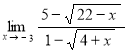 ;
;
г) ![]() ;
;
д) ![]() .
.
Решение.
а) ![]()
![]() .
.
Здесь ни числитель, ни знаменатель не имеют конечного предела, так как оба неограниченно возрастают. То есть имеем неопределённость (∞/∞). Если предварительно преобразовать аналитическое выражение под знаком предела, разделив числитель и знаменатель на переменную ![]() в старшей степени (в нашем случае
в старшей степени (в нашем случае ![]() ), то получим:
), то получим:
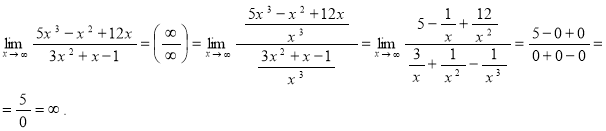
Ответ: ![]() .
.
б) ![]()
![]() .
.
Для раскрытия неопределённости (0/0) разложим числитель и знаменатель на множители, а затем сократим дробь на общий множитель (x – 2):
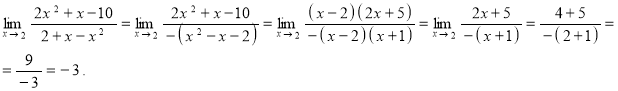
Ответ: ![]() .
.
в) 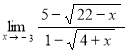
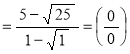 .
.
Для раскрытия неопределённости (0/0) умножим числитель и знаменатель дроби на выражение ![]() :
:
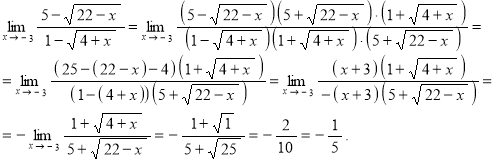
Ответ: ![]() .
.
г) ![]()
![]() .
.
Для раскрытия неопределённости (0/0) применим эквивалентные бесконечно малые функции. Так как при ![]() :
:
![]() ,
, ![]() ,
,
то:
![]()
Ответ: ![]() .
.
д) ![]()
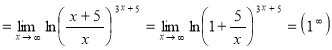 .
.
Чтобы раскрыть неопределённость (1∞), преобразуем предел так, чтобы применить второй замечательный предел в виде:
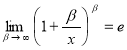 .
.
Имеем:
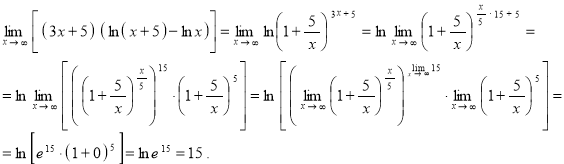
Ответ: ![]() .
.
Задание 2.
Найти точки разрыва функции y = f(x) и определить их характер. Сделать чертёж.
9 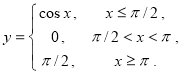
Решение.
Условие непрерывности функции в точке ![]() :
:
![]() .
.
«Подозрительными на разрыв» являются точки «внутри» областей, в которых теряется непрерывность функции (таких точек нет), и точки, в которых меняется аналитическое описание функции (![]() ).
).
Точка ![]() .
.
Предел «слева» в этой точке:
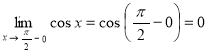 .
.
Предел «справа» в этой точке:
![]() .
.
Значение функции в этой точке:
![]() .
.
Левый и правый пределы функции конечны, равны между собой и равны значению функции в точке. Следовательно, в точке ![]() функция непрерывна.
функция непрерывна.
Точка ![]() .
.
Предел «слева» в этой точке:
![]() .
.
Предел «справа» в этой точке:
![]() .
.
Значение функции в этой точке:
![]() .
.
Левый и правый пределы функции конечны, но не равны между собой. Значит, в точке ![]() функция имеет разрыв скачка. Скачок в точке равен:
функция имеет разрыв скачка. Скачок в точке равен:
![]()
Построим схематично график функции.
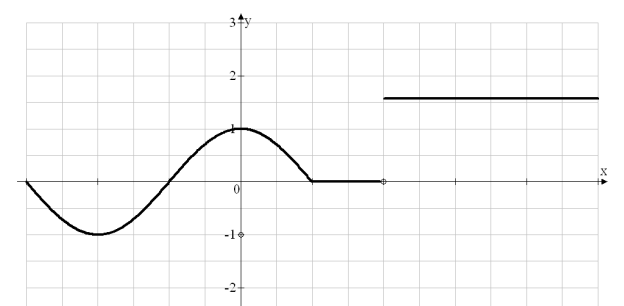
![]()
![]()
![]()
-п 0 п 2п
Ответ: функция терпит разрыв скачка в точке ![]() .
.
Задание 3.
Найти производные:
9 а) 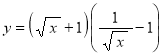 ;
;
б) ![]() ;
;
в) 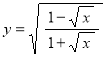 ;
;
г) ![]() ;
;
д) ![]() ;
;
е) y = ln3(1 + ex/3);
ж) x = at cost,
y = at sint.
Решение.
а) 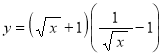 .
.
По правилу дифференцирования произведения двух функций запишем:
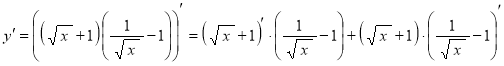 .
.
Используя правило дифференцирования суммы (разности) двух функций, а также таблицу производных, получим:
![]() ;
;
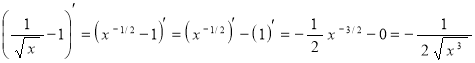 .
.
Окончательно запишем:
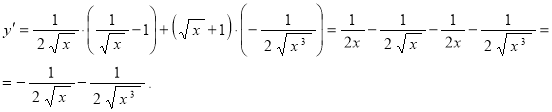 .
.
Ответ: 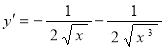 .
.
б) ![]() .
.
Постоянный множитель можно выносить за знак производной:
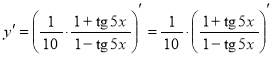 .
.
По правилу дифференцирования частного двух функций запишем:
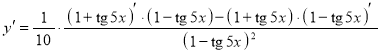 .
.
Применяя правила дифференцирования и таблицу производных, получим:
![]()
![]()
Окончательно запишем:
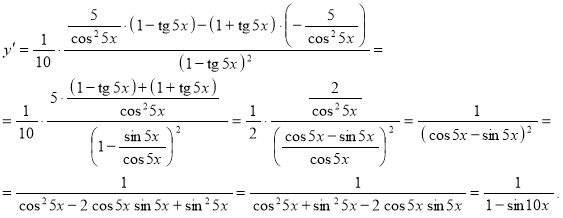
Ответ: ![]() .
.
в) 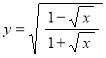 .
.
Сначала используем формулу дифференцирования сложной функции:
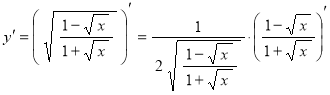 .
.
Для оставшейся производной применим формулу дифференцирования частного двух функций:
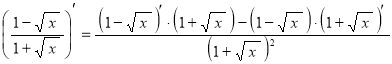 .
.
Для производных, стоящих в числителе, сначала применим правила дифферен-цирования, а затем используем таблицу производных:
![]() ;
;
![]() .
.
Окончательно получаем:
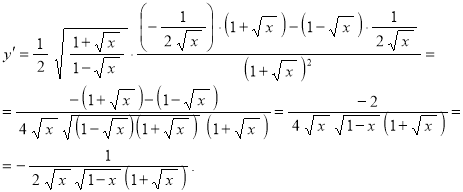
Ответ: ![]() .
.
г) ![]() .
.
Применим правило дифференцирования суммы функций:
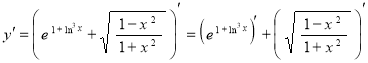 .
.
Далее используя правило дифференцирования сложной функции, а также правила дифференцирования и таблицу производных:
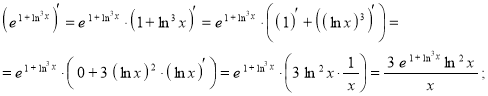
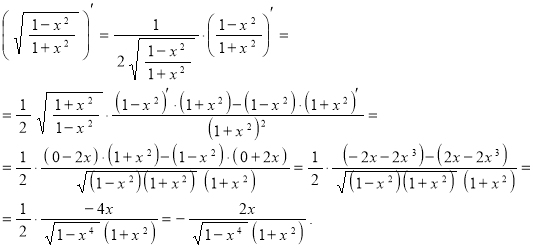
Окончательно запишем:
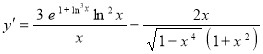 .
.
Ответ: 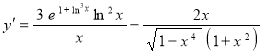 .
.
д) ![]() .
.
Применим правило дифференцирования произведения двух функций:
![]() .
.
Далее используя правило дифференцирования сложной функции, а также правила дифференцирования и таблицу производных:
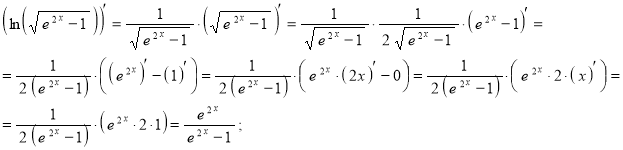
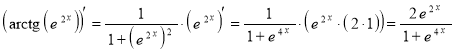 .
.
Окончательно запишем:
![]() .
.
Ответ: ![]() .
.
е) ![]() .
.
Используя правило дифференцирования сложной функции, а также правила дифференцирования и таблицу производных, получим:
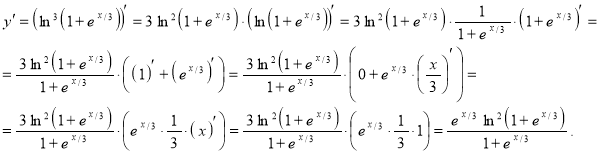
Ответ: ![]() .
.
ж) ![]()
Найдём первую производную.
Найдём производные от ![]() и
и ![]() по параметру
по параметру ![]() :
:
![]() ;
;
![]() .
.
Тогда первая производная функции будет равна:
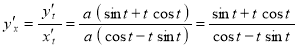 .
.
Ответ: ![]() .
.
Задание 4.
Вычислить предел, используя правило Лопиталя:
9 ![]() .
.
Решение.
Подставляем предельное значение в функцию:
![]() .
.
В данном случае имеем неопределённость (∞0).
Обозначим вычисляемый предел:
![]() .
.
Прологарифмируем это равенство:
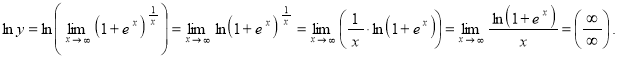
Получили неопределённость (∞/∞), значит, можем применить правило Лопиталя:
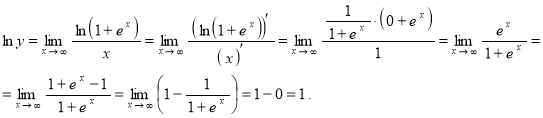
Таким образом:
![]() .
.
Следовательно:
![]() ,
,
или:
![]() .
.
Ответ: ![]() .
.
Задание 5.
Провести полное исследование функций и построить их графики:
9 а) y = (2x + 1) / x2;
б) y = (x – 1) e3x + 1.
Решение.
а) ![]() .
.
Заданная функция:
![]() , или
, или ![]() .
.
1) Область определения функции:
![]() .
.
2) ![]() – функция общего вида.
– функция общего вида.
Функция непериодическая.
3) Точки пересечения графика функции с осями координат:
с осью Оy: ![]() – точек пересечения нет;;
– точек пересечения нет;;
с осью Оx: ![]() .
.
4) Интервалы знакопостоянства функции.

![]() − + +
− + +
![]()
![]()
![]()
![]()
![]()
![]() при
при ![]() – график функции ниже оси Ox;
– график функции ниже оси Ox;
![]() при
при ![]() – график функции выше оси Ox.
– график функции выше оси Ox.
5) Асимптоты функции.
а) Вертикальные асимптоты.
Функция непрерывна в области определения. Исследуем точку ![]() :
:
![]() ;
;
![]() .
.
Таким образом, ![]() – точка разрыва функции 2-го рода.
– точка разрыва функции 2-го рода.
Следовательно, прямая ![]() – вертикальная асимптота графика функции.
– вертикальная асимптота графика функции.
б) Наклонная асимптота ![]() :
:
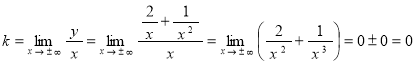 ;
;
![]() .
.
Таким образом:
наклонных асимптот нет;
прямая ![]() – горизонтальная асимптота.
– горизонтальная асимптота.
6) Определим интервалы возрастания и убывания функции, и её точки экстремума, для чего вычислим первую производную:
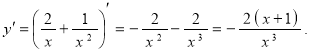
Из условия ![]() находим стационарные точки:
находим стационарные точки:
![]() ;
;
![]() не определена при
не определена при ![]() , однако, эта точка не входит в область определения.
, однако, эта точка не входит в область определения.
Точки ![]() и
и ![]() делят числовую прямую на 3 интервала. Определим знак производной на каждом интервале и укажем стрелками характер монотонности функции на диаграмме:
делят числовую прямую на 3 интервала. Определим знак производной на каждом интервале и укажем стрелками характер монотонности функции на диаграмме:

![]() − + −
− + −
![]()
![]()
![]()
![]()
![]()
![]()
Интервалы монотонности функции:
функция убывает при ![]() ;
;
функция возрастает при ![]() .
.
Точки экстремума:
минимум ![]() .
.
7) Определим интервалы выпуклости графика функции и точки перегиба, для чего вычислим вторую производную:
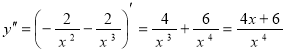
Из условия ![]() находим точки, подозрительные на перегиб:
находим точки, подозрительные на перегиб:
![]() ;
;
![]() не определена при
не определена при ![]() , однако, эта точка не входит в область определения.
, однако, эта точка не входит в область определения.
Точки ![]() и
и ![]() делят числовую прямую на 3 интервала. Определим знак второй производной на каждом интервале и укажем на ней интервалы выпуклости функции:
делят числовую прямую на 3 интервала. Определим знак второй производной на каждом интервале и укажем на ней интервалы выпуклости функции:

![]() − + +
− + +
![]()
![]()
![]()
![]()
![]()
![]()
Интервалы выпуклости функции:
график функции выпуклый вверх при ![]() ;
;
график функции выпуклый вниз при ![]() .
.
Точки перегиба:
![]() .
.
8) Найдём несколько дополнительных точек для построения графика:
|
|
|
|
|
|
|
x |
-3 |
1 |
3 |
5 |
|
y |
-5/9 |
3 |
7/9 |
11/25 |
|
|
|
|
|
|
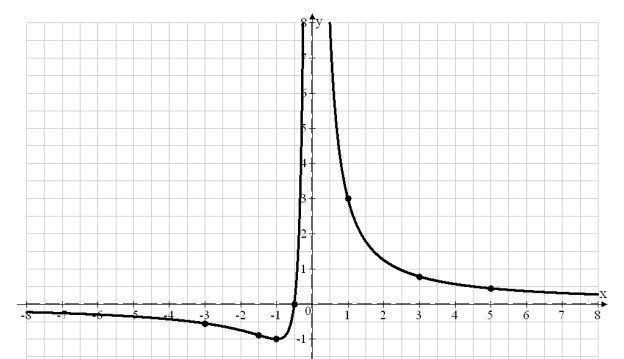
По результатам исследования строим график функции ![]() .
.
![]()
![]()
![]()
![]()
![]()
б) ![]() .
.
1) Функция определена на всей числовой прямой, то есть область определения функции:
![]() .
.
2) ![]() – функция общего вида.
– функция общего вида.
Функция непериодическая.
3) Точки пересечения графика функции с осями координат:
с осью Оy: ![]() ;
;
с осью Оx: ![]() .
.
4) Интервалы знакопостоянства функции.

![]() − +
− +
![]()
![]()
![]()
![]()
![]() при
при ![]() – график функции ниже оси Ox;
– график функции ниже оси Ox;
![]() при
при ![]() – график функции выше оси Ox.
– график функции выше оси Ox.
5) Асимптоты функции.
а) Вертикальные асимптоты.
Функция определена на всей числовой прямой – вертикальных асимптот нет.
б) Наклонная асимптота ![]() :
:
![]() ;
;
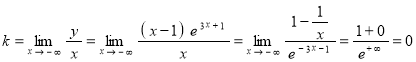 ;
;
![]() Правило Лопиталя
Правило Лопиталя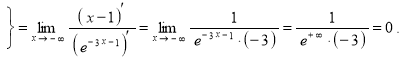
Таким образом:
наклонных асимптот нет;
![]() – горизонтальная асимптота.
– горизонтальная асимптота.
6) Определим интервалы возрастания и убывания функции, и её точки экстремума, для чего вычислим первую производную:
![]()
Из условия ![]() находим стационарные точки:
находим стационарные точки:
![]() .
.
Точек разрыва нет.
Найденная критическая точка делит числовую прямую на 2 интервала. Определим знак производной на каждом интервале и укажем стрелками характер монотонности функции на диаграмме:
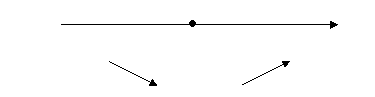
![]() − +
− +
![]()
![]()
![]()
![]()
![]()
Интервалы монотонности функции:
функция убывает при ![]() ;
;
функция возрастает при ![]() .
.
Точки экстремума:
минимум 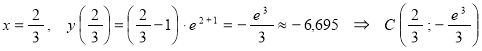 .
.
7) Определим интервалы выпуклости графика функции и точки перегиба, для чего вычислим вторую производную:
![]()
Из условия ![]() находим точки, подозрительные на перегиб:
находим точки, подозрительные на перегиб:
![]() .
.
Точек разрыва нет.
Найденная точка делит числовую прямую на 2 интервала. Определим знак второй производной на каждом интервале и укажем на ней интервалы выпуклости функции:

![]() − +
− +
![]()
![]()
![]()
![]()
![]()
Интервалы выпуклости функции:
график функции выпуклый вверх при ![]() ;
;
график функции выпуклый вниз при ![]() .
.
Точки перегиба:
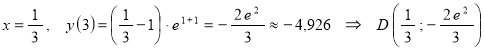 .
.
8) Построим график функции ![]() по результатам исследования.
по результатам исследования.
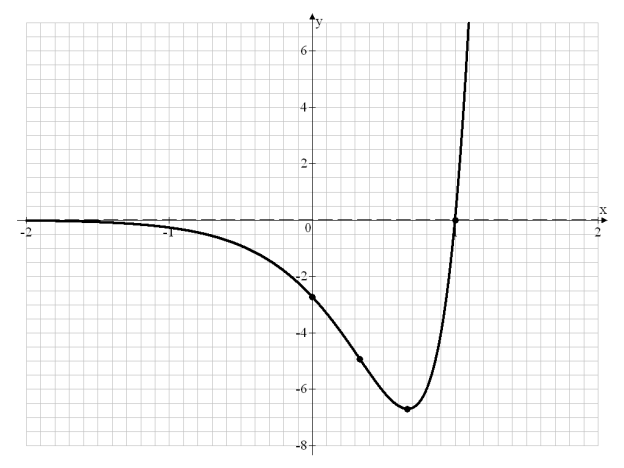
![]()
![]()
![]()
![]()
![]()
1
Имя файла: gotovoe.doc
Размер файла: 328 Kb
Если закачивание файла не начнется через 10 сек, кликните по этой ссылке
