Примеры решенных задач по математике - Контрольная 3
Ниже приведены условия и решения задач. Закачка решений в формате doc начнется автоматически через 10 секунд.
Вариант 5
Задача 1. Решить задачу Коши для дифференциального уравнения с разделяющими переменными:
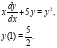
Решение: Данное уравнение является уравнением с разделяющимися переменными. Решим его:
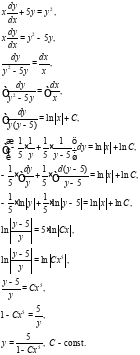
Найдем частное решение, подставив исходные данные:
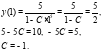
Тогда частое решение имеет вид:
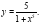
Ответ: 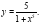
Задача 2. Найти общее решение однородного дифференциального уравнения:
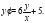
Решение: Данное уравнение является линейным однородным уравнением, которое решим с помощью замены 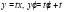 , которая приводит к уравнению с разделяющимися переменными:
, которая приводит к уравнению с разделяющимися переменными:
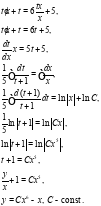
Ответ: 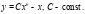
Задача 3. Найти общее решение линейного дифференциального уравнения:
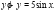
Решение:
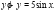
Данное уравнение является линейным неоднородным уравнением, которое решим с помощью замены 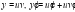
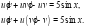
Составим и решим систему:
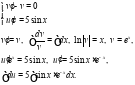
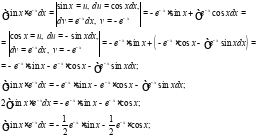
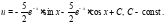
Таким образом общее решение имеет вид:
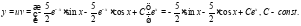
Ответ: 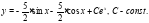
Задача 4. Найти общее решение линейного однородного дифференциального уравнения:
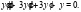
Решение: Данное уравнение является однородным дифференциальным уравнением 3го порядка.
Составим и решим характеристическое уравнение: 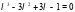 ,
, 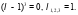
Общее решение имеет вид: 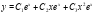 , где
, где 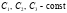 .
.
Ответ: 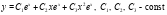
Задача 5. Найти общее решение линейного неоднородного дифференциального уравнения второго порядка:
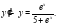
Решение: Данное уравнение является неоднородным дифференциальным уравнением 2го порядка.
Найдем общее решение соответствующего однородного уравнения: 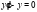 .
.
Составим и решим характеристическое уравнение: 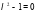 ,
, 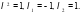
Общее решение имеет вид: 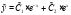 , где
, где 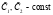 .
.
Общее решение неоднородного уравнения ищем в виде: 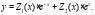
Составим систему:
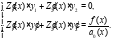
В данном случае:
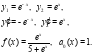
Таким образом:
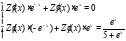
Решим систему по формулам Крамера:
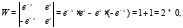
значит система имеет единственное решение.
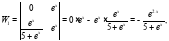
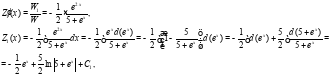
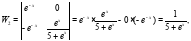
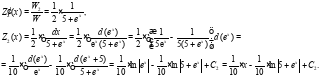
В результате общее решение исходного уравнения имеет вид:
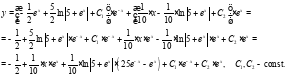
Ответ: 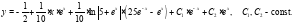
Задача 6. Найти общее решение системы линейного дифференциальных уравнений:
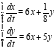
Решение:
Выразим y из первого уравнения системы:
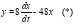
Дифференцируем по t:
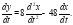
Подставим y и 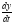 во второе уравнение системы:
во второе уравнение системы:
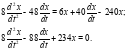
Характеристическое уравнение:
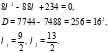
Тогда 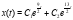 .
.
Дифференцируем по t:
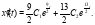
Подставим 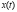 и
и 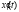 в уравнение (*):
в уравнение (*):
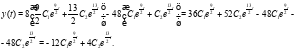
Общее решение системы:
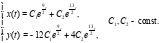
Ответ: 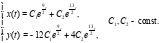
Контрольная работа № 2
Вариант 5
Задача 1. Найти частные производные функции 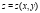 , заданной неявно:
, заданной неявно:
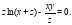
Решение:
Рассматриваем функцию трёх переменных 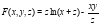 . Тогда частные производные можно найти по следующим формулам:
. Тогда частные производные можно найти по следующим формулам:
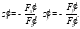
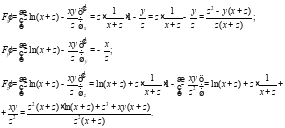
Таким образом:
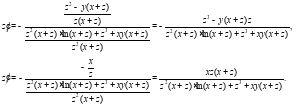
Задача 2. Построить матрицу Якоби 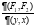 отображения, заданного системой уравнений
отображения, заданного системой уравнений
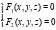
И найти производные функций 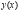 и
и 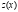 , если
, если
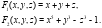
Решение:
Вычислим частные производные:
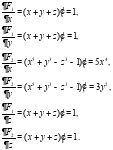
Матрица Якоби имеет вид: 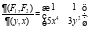
Таким образом:
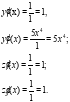
Задача 3. Найти точки локального экстремума функции:
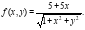
Решение: Найдем стационарные точки. Для этого найдем частные производные 1-го порядка:
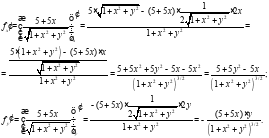
И решим систему:
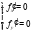
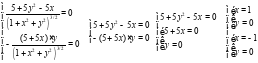
Таким образом, получили 2 стационарные точки: 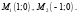
Проверим выполнение достаточного условия экстремума:
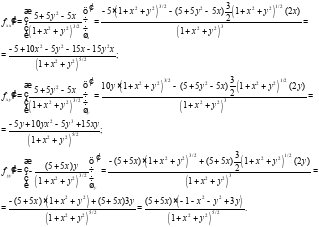
Для точки 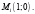
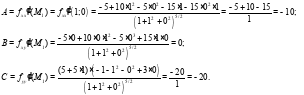
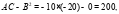 значит в точке
значит в точке 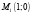 существует экстремум, так как
существует экстремум, так как 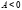 , то это максимум.
, то это максимум.
Для точки 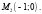
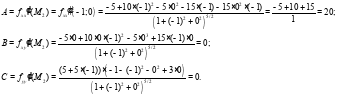
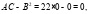 значит необходимо еще исследовать.
значит необходимо еще исследовать.
Ответ: 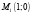 точка максимума.
точка максимума.
Задача 4. Найти решение задачи на условный экстремум методом множителей Лагранжа:
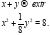
Решение:
Составим функцию Лагранжа:
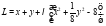
Найдём частные производные 1-го порядка:
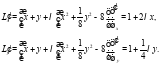
Найдём стационарные точки:
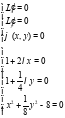
Из первых двух уравнений выразим:
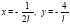 – подставим в уравнение связи:
– подставим в уравнение связи:
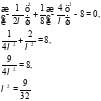
Если 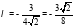
то 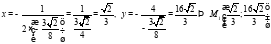
Если 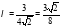
то 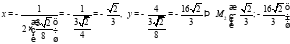
Проверим выполнение достаточного условия экстремума. Составим дифференциал второго порядка:
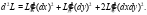
Найдём частные производные второго порядка:
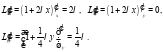
Таким образом:
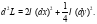
При 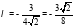
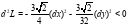 , значит, функция
, значит, функция 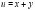 достигает условного максимума в точке
достигает условного максимума в точке 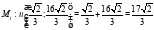 .
.
При 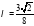
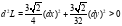 , значит, функция
, значит, функция 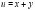 достигает условного минимума в точке
достигает условного минимума в точке 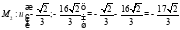 .
.
Ответ: при условии 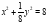 :
:
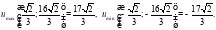
Задача 5. Найти неопределенный интеграл: 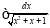
Решение:
Решим данный интеграл приведя его к табличному виду:
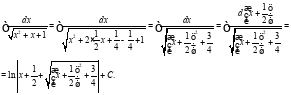
Ответ: 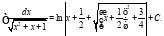
Задача 6. Вычислить определенный интеграл: 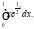
Решение:
Решим данный интеграл методом интегрирования по частям: 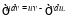
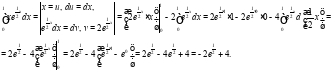
Ответ: 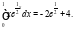
Задача 8. Исследовать на сходимость несобственный интеграл (если несобственный интеграл сходится, то найти его значение):
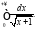
Решение:
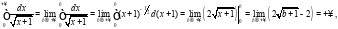
таким образом, исследуемый ряд расходится.
Ответ: ряд расходится.
Задача 8. Исследовать на сходимость числовой ряд 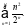
Решение:
Воспользуемся признаком Даламбера:
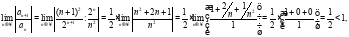
значит ряд сходится.
Ответ: ряд сходится.
Задача 9. С помощью двойного интеграла вычислить площадь плоской фигуры, ограниченной прямыми.
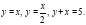
Решение: Изобразим область интегрирования на чертеже:

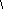
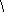
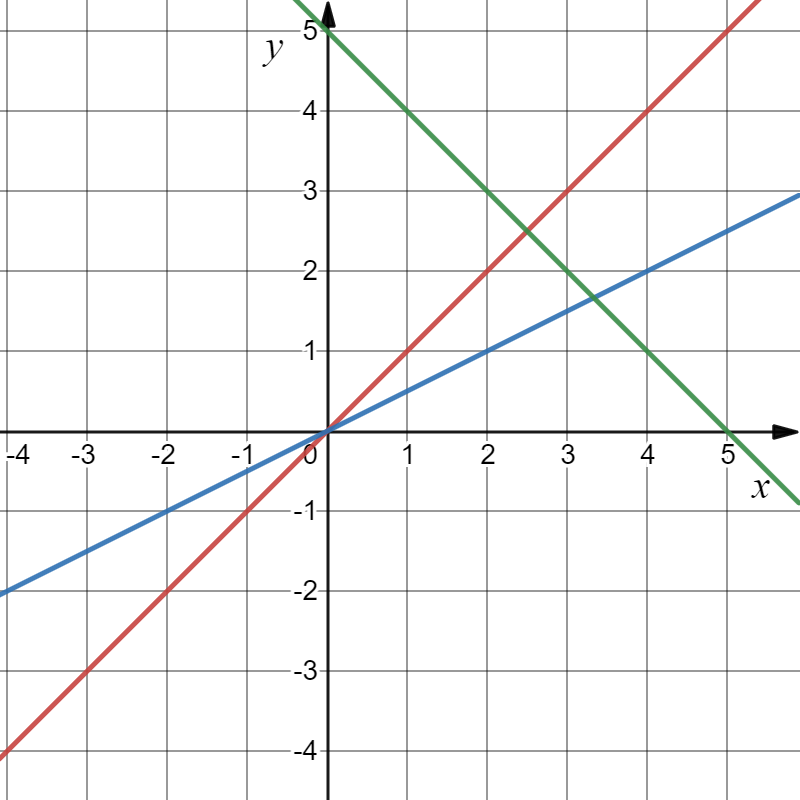
Вычислим точки пересечения прямых:
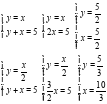
Выберем следующий порядок обхода области:
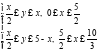
Таким образом:
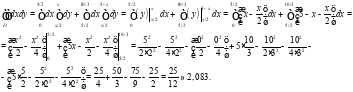
Имя файла: vyshka_var_51.docx
Размер файла: 313.33 Kb
Если закачивание файла не начнется через 10 сек, кликните по этой ссылке