Примеры решенных задач по математике - Контрольная 2
Ниже приведены условия и решения задач. Закачка решений в формате doc начнется автоматически через 10 секунд.
№394
Стрелок А поражает мишень с вероятностью 0.6, стрелок B – с вероятностью 0.5 и стрелок С – с вероятностью 0.4. Стрелки дали залп по мишени и две пули попали в цель. Что вероятнее : попал стрелок С в мишень или нет?
Дано : P(A)=0.6 ; P(B)=0.5 ; P(C)=0.4
Решение.
Введём обозначения : А – «попадание в мишень первым стрелком», B – «попадание в мишень вторым стрелком», С – «попадание в мишень третьим стрелком», D – «попадание в мишень третьим стрелком, при условии, что две пули попали в цель». Тогда, событие D можно выразить через события C, A, B, ![]() ,
, ![]() :
:
D=![]()
Так как события ![]() ,
, ![]() несовместные, то по теореме сложения вероятностей несовместных событий, получим :
несовместные, то по теореме сложения вероятностей несовместных событий, получим :
P(D)=![]()
Так как события А, B, С независимы, то по теореме умножения вероятностей независимых событий, получим :
P(D)=![]()
где P(![]() )=1-P(A)=1-0.6=0.4 ; P(
)=1-P(A)=1-0.6=0.4 ; P(![]() =1-P(B)=1-0.5=0.5
=1-P(B)=1-0.5=0.5
P(D)=0.6×0.5×0.4+0.4×0.5×0.4=0.2
Найдём вероятность события ![]() - «стрелок С не попал в мишень, при попадании двух пуль», противоположного событию D :
- «стрелок С не попал в мишень, при попадании двух пуль», противоположного событию D :
P(![]() )=P(AB
)=P(AB![]() )=P(A)P(B)P(
)=P(A)P(B)P(![]() )=0.6×0.5×0.6=0.18
)=0.6×0.5×0.6=0.18
где P(![]() )=1-P(С)=1-0.4=0.6
)=1-P(С)=1-0.4=0.6
Так как P(D)>P(![]() ) , то попадание стрелка С в мишень при одном залпе, при условии, что в мишень попало две пули, вероятнее, чем промах.
) , то попадание стрелка С в мишень при одном залпе, при условии, что в мишень попало две пули, вероятнее, чем промах.
Ответ : попадание стрелка С в мишень более вероятно, чем промох.
№ 404
Задана непрерывная случайная величина X своей плотностью распределения вероятностей f(x) . Требуется :
1) определить коэффициент А ;
2) найти функцию распределения F(x) ;
3) схематично построить графики функций f(x) и F(x) ;
4) вычислить математическое ожидание и дисперсию X;
5) определить вероятность того, что X примет значение из интервала (a, b).
Дано : f(x)=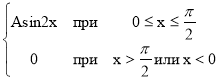 ; a=
; a=![]() ; b=
; b=![]()
Решение.
1) Определим коэффициент А. Поскольку все значения данной случайной величины заключены на отрезке [0 ; π/2], то
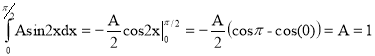
2) Найдём функцию распределения F(x), с помощью отношения 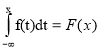
При x≤0 имеем :
F(x)=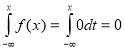
При 0<x<![]() имеем : F(x)=
имеем : F(x)=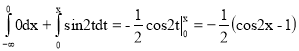
При x>![]() получаем :
получаем :
F(x)=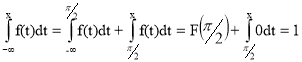
Таким образом, получаем :
F(x)=
3) на рисунке построены графики f(x) и F(x).
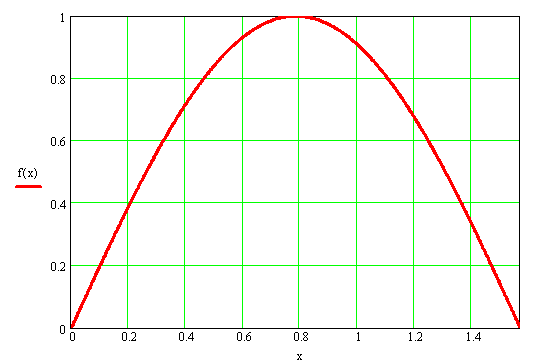
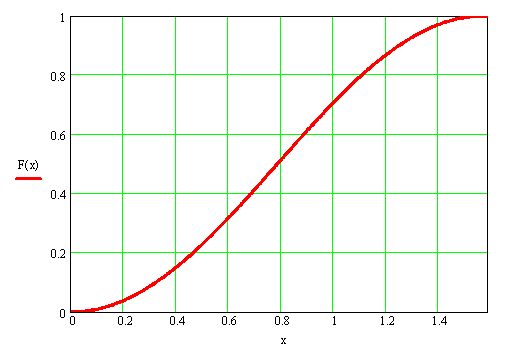
4) вычислим математическое ожидание и дисперсию X.
Математическое ожидание по формуле :
M(x)=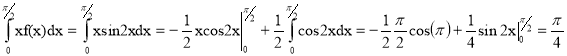
Находим дисперсию непрерывной случайной величины.
M(X2)=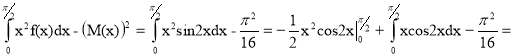
=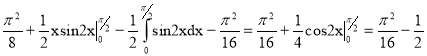
5) определим вероятность того, что X примет значение из интервала (a, b).
Вероятность того, что X примет значение из интервала ![]() , находим следующим образом : P
, находим следующим образом : P![]() =F
=F![]() -F
-F![]() =-
=-![]()
Ответ : 1) A=1 ; 2) F(x)=  ; 3) M(X)=
; 3) M(X)=![]() ; 4) D(X)=
; 4) D(X)=![]() ; 5) P
; 5) P![]() .
.
№ 414
Нормально распределённая случайная величина X задана своими параметрами а ( математическое ожидание) и σ (среднее квадратическое отклонение). Требуется :
а) написать плотность вероятностей и схематически изобразить график ;
б) найти вероятность того, что X примет значение из интервала (α;β) ;
в) найти вероятность того, что X отклонится (по модулю) от а не более, чем на δ ;
г) применяя правило «трёх сигм» найти значения случайной величины X.
Дано : a=4 , σ=2, α=5 , β=6 , δ=4.
Решение.
а) плотность вероятности нормально распределённой случайной величины имеет вид :
f(x)=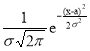 , где а – математическое ожидание ; σ – среднее квадратическое отклонение.
, где а – математическое ожидание ; σ – среднее квадратическое отклонение.
В нашем случае а=4, σ=2, тогда : f(x)=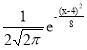
Изобразим график функции f(x) :
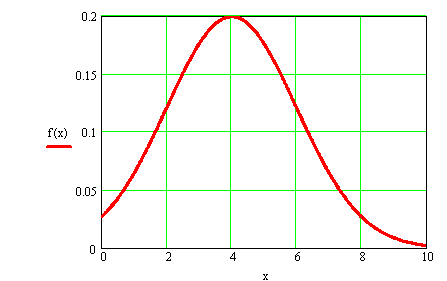
б) найдём вероятность того, что X примет значение из интервала (α;β) ;
P(α<X<β)=Ф![]() - Ф
- Ф![]()
P(5<X<6)=Ф![]() - Ф
- Ф![]() =Ф(1) – Ф(0.5)
=Ф(1) – Ф(0.5)
По таблице значений функции Лапласа находим Ф(1)=0.3413 ; Ф(0.5)=0.1915
Тогда : P(5<X<6)=0.3413 - 0.1915=0.1498
в) найдём вероятность того, что X отклонится (по модулю) от а не более, чем на δ ;
Воспользуемся формулой : P(|X-a|<δ)=2Ф(δ/σ)
В нашем случае : P(|X-4|<4)=2Ф(4/2)=2Ф(2)=2×0.4772=0.9544
где Ф(2)=0.4772
г) применяя правило «трёх сигм» найдём значения случайной величины X.
Из равенства : P(|X-a|<3σ)=0.9973
Из неравенства : |X-4|<3 получаем -3<X-4<3 ; 4-3<X<4+3 ; 1<X<7
Значит значения случайной величины X лежат в интервале : (1 ; 7)
Ответ : а) f(x)=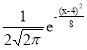 ; б) P(5<X<6)=0.1498 ; в) P(|X-4|<4)=0.9544 ; г) X∈(1 ; 7).
; б) P(5<X<6)=0.1498 ; в) P(|X-4|<4)=0.9544 ; г) X∈(1 ; 7).
№ 424
АТС имеет к линий связи. Поток вызовов – простейший с интенсивностью λ вызовов в минуту. Среднее время переговоров составляет t мин. Время переговоров распределено по показательному закону. Найти : 1) абсолютную и относительную пропускные способности АТС ; 2) вероятность того, что все линии связи заняты ; 3) среднее число занятых линий связи ; 4) определить, имеет ли АТС число линий связи, достаточное для того, чтобы вероятность отказа не превышала α.
Дано : k=5 ; λ=0.7 ; t=3.5 ; α=0.05
Решение.
1) найдём абсолютную и относительную пропускные способности АТС.
Так как время переговоров распределено по показательному закону и среднее время переговоров t, то пропускная способность одной линии : a=1/t. Пропускная способность АТС, имеющей к линий : k/t=5/3.5=1.4 1/мин. Относительная пропускная способность : δ=k/(tλ)=
=1.4/(0.8×3.5)=0.5
2) вероятность того, что все линии связи заняты
Вероятность того, что все линии связи заняты , равна вероятности того, что за 1 мин поступит пять вызовов. Для этого воспользуемся формулой Пуассона :
Pt(k)=![]()
В нашем случае : P1(5)=![]() =0.0007
=0.0007
3) среднее число занятых линий связи
Среднее число занятых линий равно среднему числу вызовов : N=1/λ=1/0.7=1.43
4) определить, имеет ли АТС число линий связи, достаточное для того, чтобы вероятность отказа не превышала α.
Так как вероятность того, что хотя бы одна линия связи свободна P1(k≥1)=1-P1(5)=
=1-0.0007=0.9993 больше чем вероятность безотказного прохождения вызова p=1-α=
=1-0.05=0.95, то АТС имеет число линий, достаточное для того, чтобы вероятность отказа не превышала 0.05.
Ответ : 1) a=1.4 ; δ=0.5 ; 2) P1(5)=0.0007 ; 3) N=1.43 ; 4) число линий АТС , достаточно для того, чтобы вероятность отказа не превышала 0.05.
Имя файла: mat2.doc
Размер файла: 152.5 Kb
Если закачивание файла не начнется через 10 сек, кликните по этой ссылке
