Пример решенной контрольной работы по теории вероятностей
2.
Найдем вероятность, что были извлечены только белые шары (событие А):
.
Найдем вероятность, что были извлечены только синие шары (событие В):
.
Найдем вероятность, что были извлечены только красные шары (событие С):
.
События А, В, С несовместны, тогда по теореме сложения вероятностей вероятность извлечь шары одного цвета 
.
3.
Событие А – взятые 2 изделия оказались годными. Рассмотрим возможные гипотезы:
– в партии нет деталей с дефектами: 
, 
;
– в партии одна деталь с дефектом: 
, 
;
– в партии две детали с дефектом: 
, 
;
– в партии три детали с дефектом: 
, 
.
По формуле Байеса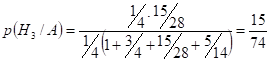 
.
4.
Стрельба на каждом рубеже удовлетворяет схеме Бернулли с параметрами 
, 
для 1-го рубежа и 
для 2-го рубежа.
Пусть событие А – оба рубежа преодолены без промахов, тогда по теореме умножения вероятностей 
.
Пусть событие В – оба рубежа преодолены с одним промахом, тогда по теореме умножения вероятностей 
.
Пусть событие С – биатлонист допустил 1 промах. Промахи на каждом из рубежей являются совместными событиями, поэтому по теореме сложения вероятностей 
.
Пусть событие D – на первом рубеже допущен 1 промах, на втором – 2 промаха, тогда по теореме умножения вероятностей
.
5. ДСВ Х принимает значения от 2 до 4, т.к. необходимо извлечь минимум 2 шара, а среди 4-х шаров точно найдется пара одного цвета.
, т.е. извлечено подряд два шара одного цвета. 
, т.к. из оставшихся 8 шаров подходят только два.
, т.е. следующим извлечен непарный по цвету шар, а потом – парный к одному из двух. Тогда 
.
, т.е. последующие два шара должны быть непарными по цветам, а последний будет гарантированно парным к одному из них. Тогда 
.
Выполним проверку условия нормировки: 
.
Составим табличный закон распределения ДСВ Х:
|
Х |
2 |
3 |
4 |
|
р |
|
|
|
Найдем математическое ожидание ДСВ Х: 
.
6.
По свойству функции плотности распределения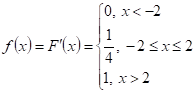 
.
Построим графики 
и 
.
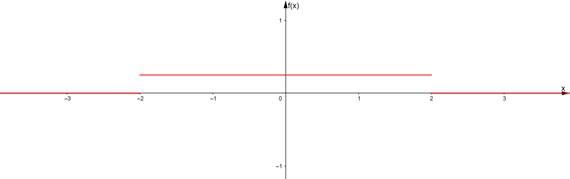
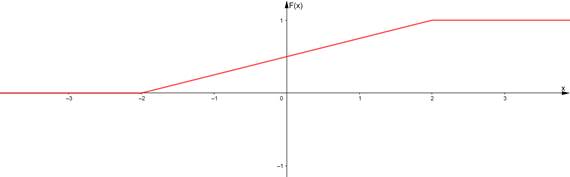
Найдем характеристики НСВ Х:
(как интеграл от нечетной функции по симметричному промежутку);
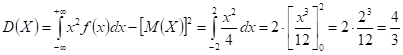(использовано свойства интеграла от четной функции по симметричному промежутку);
.
По свойству функции распределения 
.