Пример решенной контрольной работы по аналитической геометрии

Вариант 11

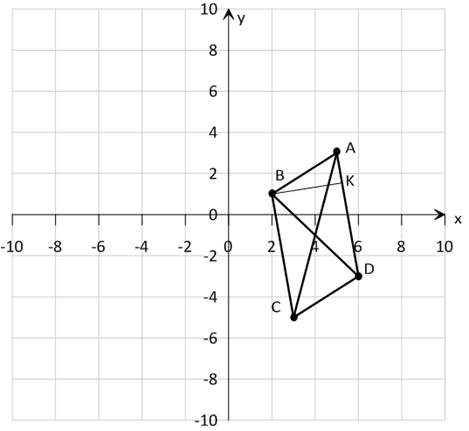
Задача 1. Даны три последовательные вершины параллелограмма

А(5; 3), В(2; 1),С(3; -5). Не находя координаты вершины D, найти:

1)    уравнение стороны AD;

2)    уравнение высоты BK, опущенной из вершины В на сторону AD;

3)    длину высоты BK;

4)    уравнение диагонали BD;

5)    тангенс угла между диагоналями параллелограмма.

Записать общие уравнения найденных прямых. Построить чертеж.

Решение

1) Уравнение прямой, проходящей через две заданные точки, имеет вид

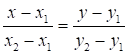
Найдем уравнение прямой BС:

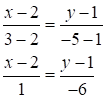
Запишем полученное уравнение в общем виде:

Запишем уравнение с угловым коэффициентом:

Воспользуемся тем фактом, что противоположные стороны параллелограмма параллельны. Составим искомое уравнение прямой AD как уравнение прямой, проходящей через точку А параллельно прямой ВС.

Угловые коэффициенты прямых AD и ВС совпадают, следовательно, можно записать:

Подставим координаты точки А и получим уравнение прямой с угловым коэффициентом:

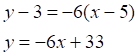   (AD)

Составим уравнение прямой в общем виде:

2) Из условия перпендикулярности двух прямых найдем угловой коэффициент

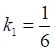
Подставим в уравнение  координаты точки В:

 

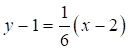
Запишем уравнение высоты BK в общем виде:

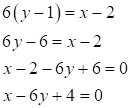
Запишем это же уравнение в виде с угловым коэффициентом: 

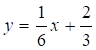 (ВК)

3) Расстояние от точки до прямой найдем по формуле:

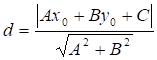
По условию В(2; 1), прямая AD определяется уравнением

Таким образом, длина высоты BK равна:

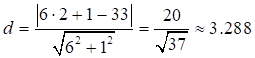
4) Обозначим Е - середина отрезка АС.

Координаты середины отрезка найдем по формуле:

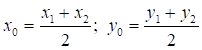
Подставим координаты точек А(5; 3) и С(3; -5):

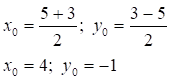
Следовательно .

Найдем уравнение прямой ВЕ:

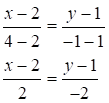
Запишем это уравнение в общем виде:

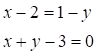
Запишем это же уравнение в виде с угловым коэффициентом:  (ВD)

5) Найдем уравнение диагонали АС:

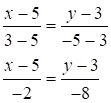
Общее уравнение:

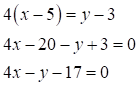
Уравнение с угловым коэффициентом имеет вид:

Угловой коэффициент k₁ = 4

Уравнение диагонали BD имеет вид

Угловой коэффициент k₂ = -1

Тангенс угла φ между двумя прямыми определяется формулой

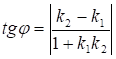
Следовательно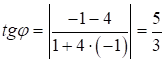

Отсюда: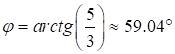

 

Задача 2. Даны точки A(2; -3; -2), B(-1; 3; 0), C(-2; 0; 1), D(4; -1; 3). Найти:

1)  общее уравнение плоскости АВС;

2)  общее уравнение плоскости, проходящей через точку D параллельно плоскости АВС;

3)  расстояние от точки D до плоскости ABC;

4)  канонические уравнения прямой АD;

5)  канонические уравнения прямой, проходящей через точку B параллельно прямой AD;

6)  синус угла между плоскостью ABC и прямой AD.

Решение

1)  Уравнение плоскости, проходящей через три заданные точки, имеет вид:

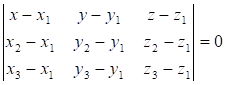
Найдем общее уравнение плоскости АВС:

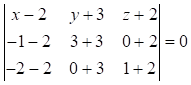  или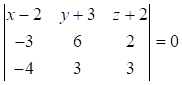

Раскроем определитель по первой строке:

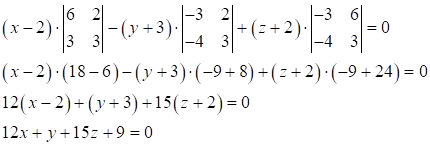
Получили уравнение плоскости АВС:

2)  Уравнение плоскости, проходящей через заданную точку, имеет вид:

Подставим координаты точки D:

В качестве нормального вектора плоскости можно взять вектор

Таким образом, запишем общее уравнение плоскости, проходящей через точку D параллельно плоскости АВС.

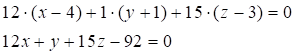
3)  Расстояние от точки D до плоскости ABC найдем по формуле: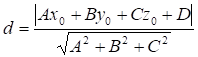

Следовательно

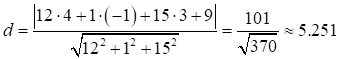
4)  Уравнения прямой, проходящей через точки, имеют вид:

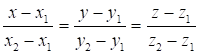
Найдем канонические уравнения прямой АD.

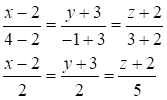
5)  Канонические уравнения прямой имеют вид: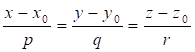

Подставим координаты точки В:

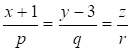
В качестве направляющего вектора можно взять вектор

Следовательно, канонические уравнения прямой, проходящей через точку B параллельно прямой AD, имеет вид:

6)  Угол между прямой и плоскостью определяется формулой:

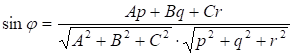
Найдем синус угла между плоскостью ABC и прямой AD.

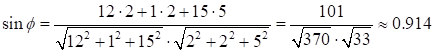
Ответ: 1) ;

2) ;

3) ;

4) ;

5) ;

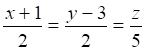6) .

 

Задача 3. Уравнение кривой второго порядка   путем выделения полного квадрата привести к каноническому виду. Построить кривую.

Решение

Сгруппируем слагаемые:

Выделим полный квадрат:

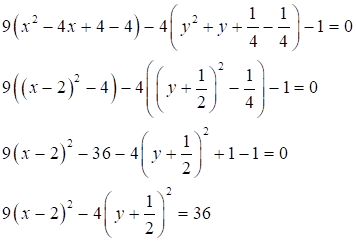
Разделим обе части равенства на 36:

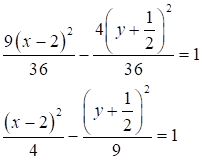
Выполним параллельный перенос осей координат по формулам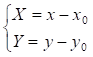

При таком преобразовании начало координат переносится в точку , уравнение эллипса принимает канонический вид .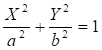

В нашем примере

Итак, рассматриваемое уравнение определяет гиперболу с центром в точке 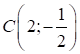  и полуосями а = 2  и b = 3.

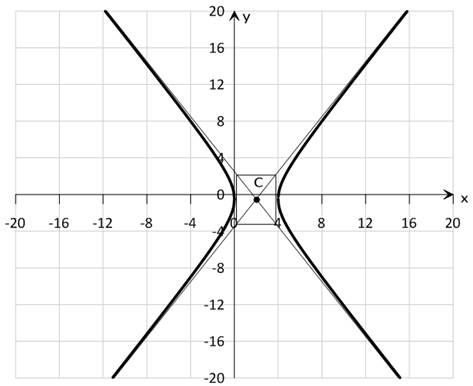
Ответ: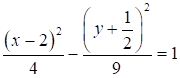

 

Задача 4. Кривая задана в полярной системе координат уравнением .

Требуется:

1)    найти точки, лежащие на кривой, давая  значения через промежуток, равный , начиная от  до ;

2)    построить полученные точки;

3)    построить кривую, соединив построенные точки (от руки или с помощью лекала);

4)    составить уравнение этой кривой в прямоугольной декартовой системе координат.

Решение

Сначала построим таблицу значений j и r.

j	0
r	0,00	0,20	0,39	0,59	0,79	0,98	1,18	1,37	1,57

 

j
r	1,77	1,96	2,16	2,36	2,55	2,75	2,95	3,14

 

Построим все точки, определенные в таблице и соединим их линией.

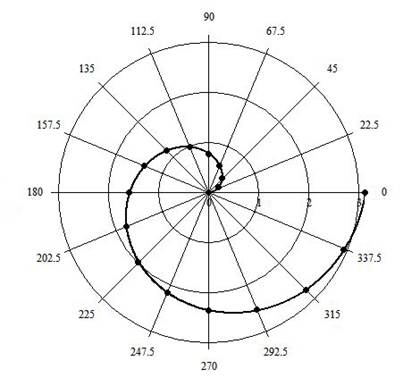
Запишем уравнение рассматриваемой кривой в прямоугольной декартовой системе координат. Воспользуемся формулами перехода от декартовой к полярной системе координат.

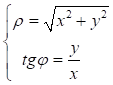
Получаем

 

Задача 5. Построить на плоскости геометрическое место точек, определяемое неравенствами

1)  ;

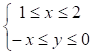2)  .

Решение

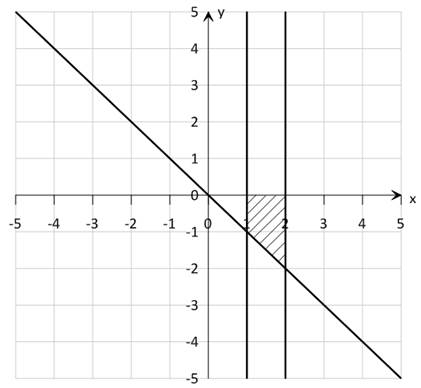
1) 

Построим прямые х = 1 и х = 2 и заштрихуем область между ними.

Построим прямую y = -x.

Заштрихуем область, лежащую ниже оси ОХ и выше прямой y = -x.

Пересечение всех заштрихованных областей и определит множество точек, представляющих решение рассматриваемой системы.

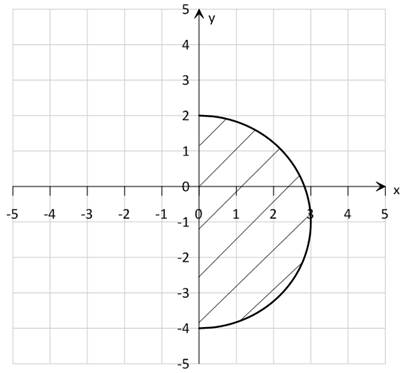
2) 

Построим линию, определяемую уравнением

 

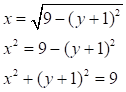
Получили уравнение окружности с центром в точке (0;-1) и радиуса 3.

Эта линия представляет собой ту часть окружности, на которой

Решением рассматриваемого двойного неравенства является часть плоскости, расположенная между осью ОY и окружностью .