Пример решенной контрольной по линейной алгебре
Задание №1
Дана матрица ![]() . Найти:
. Найти:
1) Базис линейной оболочки строк матрицы ![]()
2) Базис пространства решений системы ![]()
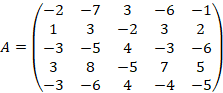
Решение:
Элементарными преобразованиями над строками матрицы приведем ее к ступенчатому виду:
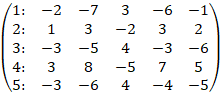
Поменяем местами первую и вторую строки:
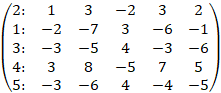
Умножим первую строку на 2 и сложим со второй, умножим первую строку на 3 и сложим с третьей, умножим первую строку на (-3) и сложим с четвертой, умножим первую строку на 3 и сложим с пятой
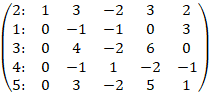
Умножим вторую строку на 4 и сложим с третьей, умножим вторую строку на (-1) и сложим с четвертой, умножим вторую строку на 3 и сложим с пятой
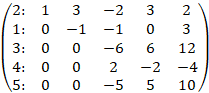
Разделим третью строку на (-6), разделим четвертую строку на 2, разделим пятую строку на (-5)
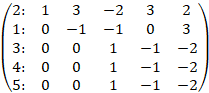
Умножим третью строку на (-1) и сложим с четвертой, умножим третью строку на (-1) и сложим с пятой
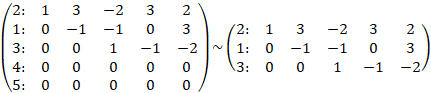
Строки матрицы 1, 2, 3 линейно независимы. Ранг матрицы равен 3, переменных 5, значит, базис пространства решений состоит из двух векторов. Примем переменные ![]() за базисные, а переменные
за базисные, а переменные ![]() за свободные. Выразим базисные переменные через свободные:
за свободные. Выразим базисные переменные через свободные:
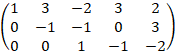
Сложим третью и вторую строки, умножим третью строку на 2 и сложим с первой
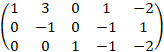
Умножим вторую строку на (-1)
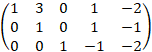
Умножим вторую строку на (-3) и сложим с первой
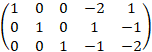
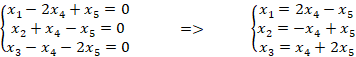
Положим ![]() получим первый базисный вектор пространства решений:
получим первый базисный вектор пространства решений:
![]()
Положим ![]() получим второй базисный вектор пространства решений:
получим второй базисный вектор пространства решений:
![]()
Задание №2
Найти координаты столбца ![]() в ортогональном базисе:
в ортогональном базисе: ![]()
![]() .
.
Решение:
1) 1 способ
Представим вектор ![]() в виде линейной комбинации векторов
в виде линейной комбинации векторов ![]()
![]()
![]()
![]()
Последнему равенству соответствует система уравнений:
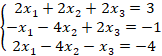
Решим систему уравнений по формулам Крамера:
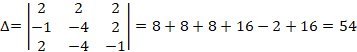
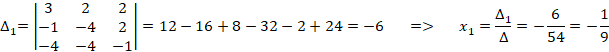
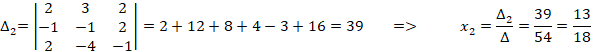
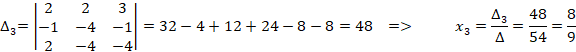
![]()
2) Способ 2
Так как базис ортогональный, то координаты вектора ![]() в базисе
в базисе ![]() можно найти по формулам:
можно найти по формулам:
![]()
![]()
![]()
Задание №3
Даны столбцы ![]() и
и ![]() . Найти столбец
. Найти столбец ![]() , ортогональный
, ортогональный ![]() так, чтобы линейные оболочки
так, чтобы линейные оболочки ![]() и
и ![]() совпадали.
совпадали.
Решение:
Найдем вектор ![]() , применяя процесс ортогонализации:
, применяя процесс ортогонализации:
![]()
![]()
Учитывая, что вектор ![]() есть линейная комбинация векторов
есть линейная комбинация векторов ![]() и
и ![]() , то
, то ![]()
Аналогично, вектор ![]() есть линейная комбинация векторов
есть линейная комбинация векторов ![]() и
и ![]() , поэтому
, поэтому ![]()
Откуда получаем, что ![]()
Задание №4
Запишите матрицу линейного оператора ![]() в базисе
в базисе ![]() , если известно, что
, если известно, что ![]() ,
, ![]()
Решение:
![]() -ый столбец матрицы оператора
-ый столбец матрицы оператора ![]() в базисе
в базисе ![]() равен столбцу координат элемента
равен столбцу координат элемента ![]() в этом базисе:
в этом базисе:
![]()
![]()
![]()
Получаем

Задание №5
В стандартном базисе пространства ![]() найти матрицу оператора
найти матрицу оператора ![]() , если
, если
![]() , где
, где ![]()
Решение:
Найдем образы базисных векторов ![]()
![]()
![]()
![]()
![]() -ый столбец матрицы оператора
-ый столбец матрицы оператора ![]() в стандартном базисе равен столбцу координат элемента
в стандартном базисе равен столбцу координат элемента ![]() в этом базисе:
в этом базисе: