Неопределенные и определенные интегралы.

№1.8. Вычислить  неопределенный интеграл

Решение.

Для вычисления данного интеграла будем использовать формулу интегрирования по частям

Обозначим: , . Тогда

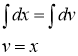
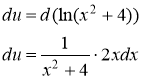
В итоге получим

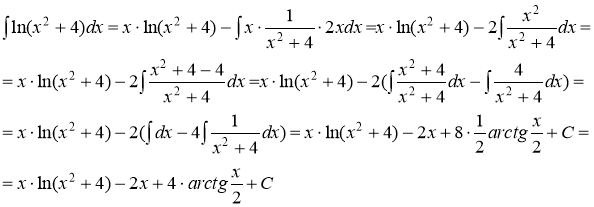
Ответ:

 

№2.8. Вычислить  определенный интеграл

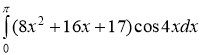
Решение.

 

Используем метод интегрирования по частям:

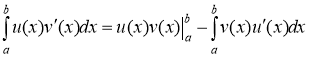
Обозначим: , . Найдем v 

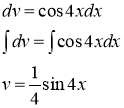
Найдем :

Тогда

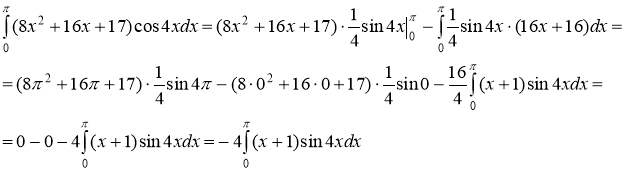Для вычисления интеграла опять применим метод интегрирования по частям

  Обозначим: , . Найдем v 

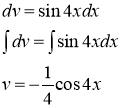
Найдем :

Тогда

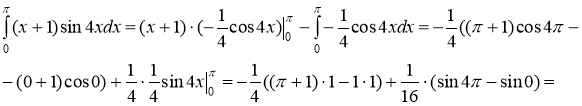
Тогда исходный интеграл равен

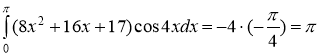
Ответ:

 

№3.8. Вычислить  неопределенный интеграл

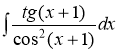
Решение.

Так как 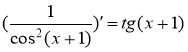, то используем теорему о «замене типа подведение под знак дифференциала»

 , где t = g(x)

В данном случае . Тогда

 

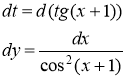
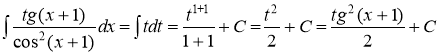
Ответ: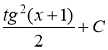

 

 

 

 

№4.8. Вычислить определенный интеграл

 

Решение.

Выполним замену переменной , тогда

При x=1  

При x= 4 

Переходя к новой переменной, получаем

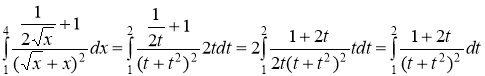
Введем новую переменную . Тогда

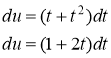
При  

При  

Тогда

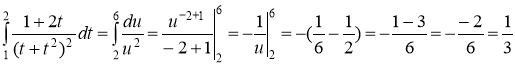
Ответ:

 

 

 

 

№5.8. Найти неопределенный интеграл

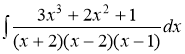
Решение.

Разделим числитель на знаменатель , в итоге получим

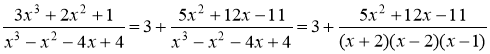
Представим дробь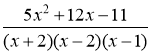 в виде суммы элементарных дробей

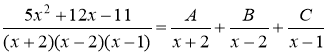
Приведя правую часть последнего равенства к общему знаменателю и приравняв числители дробей, получим тождество:

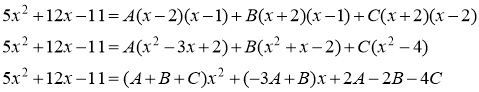
Найдём искомые коэффициенты:

              

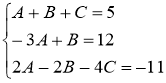
- умножим первую строку на 4 и прибавим к 3-ей

  

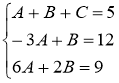
- умножим вторую строку на -2 и прибавим к 3-ей

  

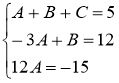
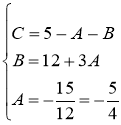
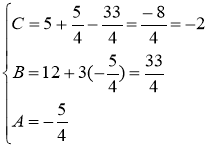
Подставив найденные коэффициенты в разложение подынтегральной функции на простейшие дроби, получим:

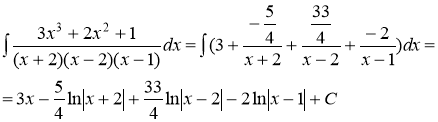
Ответ:

№8.8. Вычислить определенный интеграл

 

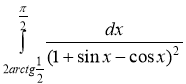
Решение.

Применяем подстановку , тогда ,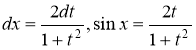

При x=   

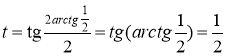
При x=  

Переходя к новой переменной, получаем

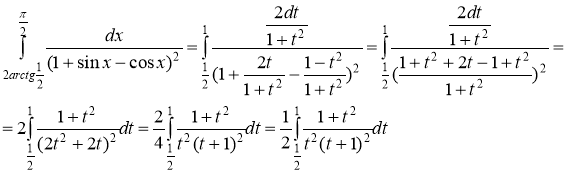
Представим дробь 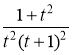в виде суммы элементарных дробей

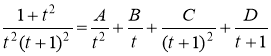
Приведя правую часть последнего равенства к общему знаменателю и приравняв числители дробей, получим тождество:

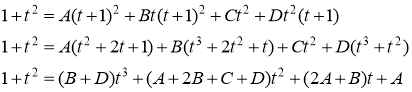
Найдём искомые коэффициенты:

        

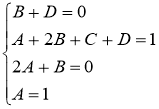
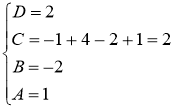
Подставив найденные коэффициенты в разложение подынтегральной функции на простейшие дроби, получим:

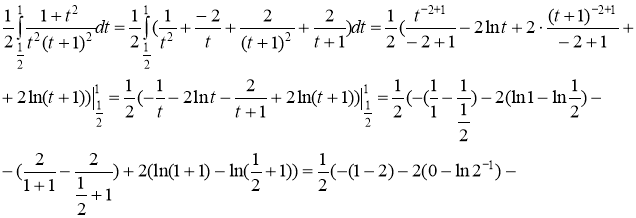
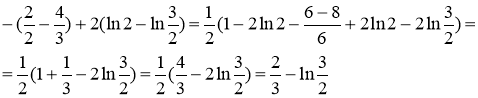
Ответ:

 

№9.8. Вычислить определенный интеграл

 

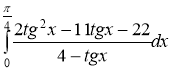
Решение.

Применяем подстановку , тогда

При x= 0  

При x=  

Переходя к новой переменной, получаем

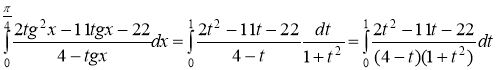
Представим дробь 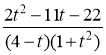в виде суммы элементарных дробей

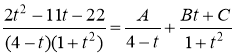
Приведя правую часть последнего равенства к общему знаменателю и приравняв числители дробей, получим тождество:

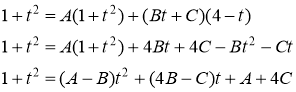
Найдём искомые коэффициенты:

        

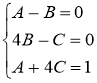
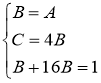
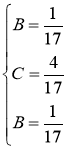
Подставив найденные коэффициенты в разложение подынтегральной функции на простейшие дроби, получим:

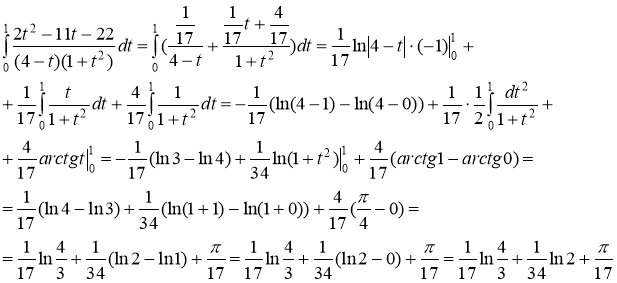
Ответ:

 

№10.8. Вычислить определенный интеграл

 

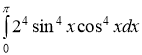
Решение.

Так как , то

Так как , то

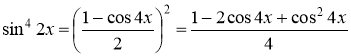
Так как , то

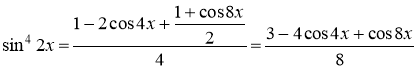
Тогда

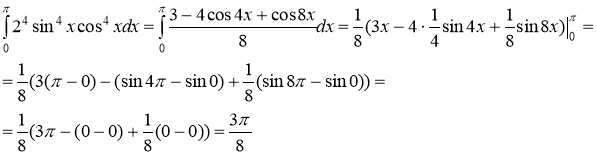
Ответ: