Линейная алгебра.
Ниже приведены условия и решения задач. Закачка решений в формате doc начнется автоматически через 10 секунд.
Вариант 4
№1 Вычислить![]() , если
, если
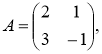
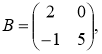
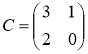
Решение.
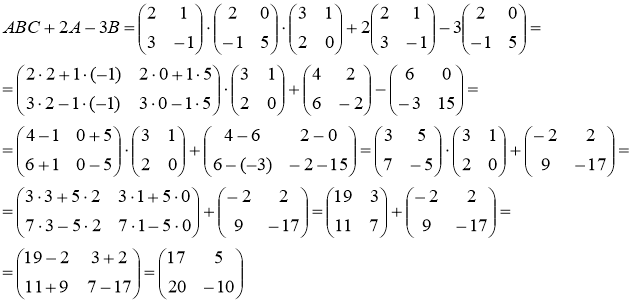 Ответ:
Ответ: 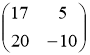
№2 Вычислить![]() и
и![]() , если
, если
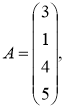
![]()
Решение.
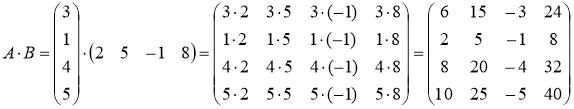
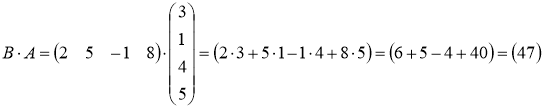
Ответ: 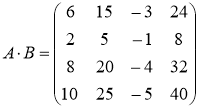 ,
, ![]()
№3 Вычислить
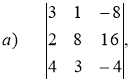
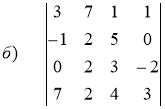
Решение.
а) Вычислим определитель методом треугольников
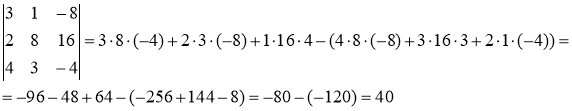
б) Вычислим определитель, получив предварительно нули в 1-ой строке.
Умножим третий столбец определителя на -3 и прибавим к первому, умножим третий столбец определителя на -7 и прибавим ко второму, умножим третий столбец определителя на -1 и прибавим к четвертому. Тогда в первой строке все элементы, кроме одного, будут нулями.
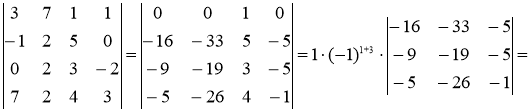
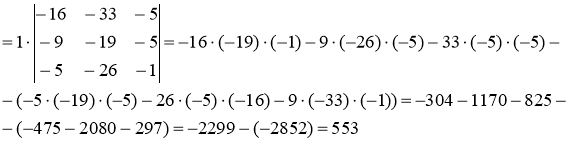
Ответ: а) 40, б) 553
№4 Найти ранг матрицы
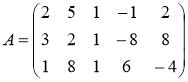
Решение.
Ранг матрицы – это наивысший порядок минора, отличного от нуля.
Исходя из определения ранга матрицы, будем искать минор наивысшего порядка, отличный от нуля. Сначала преобразуем матрицу к более простому виду. Для этого первую строку матрицы умножим на -![]() и прибавим ко второй и третьей строкам:
и прибавим ко второй и третьей строкам:
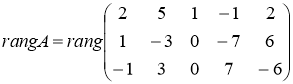
-разделим третью строку на -1
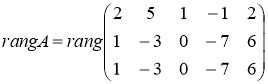
Поскольку вторая и третья строки пропорциональны, то одну из них можно вычеркнуть, что не изменит ранг. Получаем 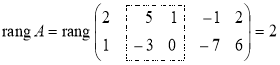 , так как в матрице есть минор второго порядка, отличный от нуля, а миноры более высокого порядка отсутствуют.
, так как в матрице есть минор второго порядка, отличный от нуля, а миноры более высокого порядка отсутствуют.
Ответ: ранг матрицы равен 2
№5 Найти матрицу, обратную данной

Решение.
Найдем обратную к матрице A матрицу A-1 по формуле
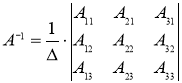
Вычислим определитель матрицы
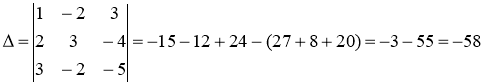
![]() Найдем алгебраические дополнения
Найдем алгебраические дополнения
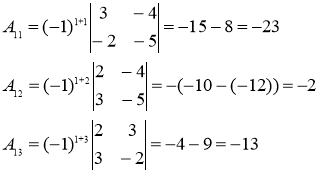
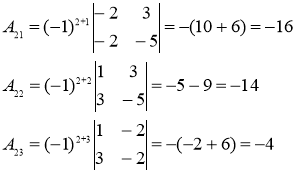
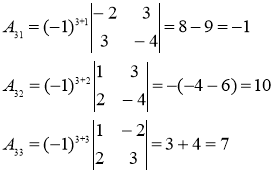
Обратная матрица
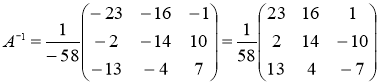
Ответ: 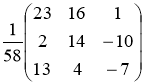
№6 а) Решить системы: а) по формулам Крамера, б) матричным способом
а) 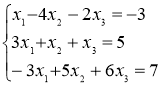 б)
б) 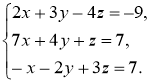
Решение.
а)
Находим главный определитель системы
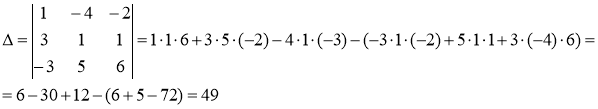
Находим вспомогательные определители ![]() , полученные заменой в определителе
, полученные заменой в определителе ![]() столбца из коэффициентов при неизвестном
столбца из коэффициентов при неизвестном ![]() , столбцом свободных членов системы
, столбцом свободных членов системы
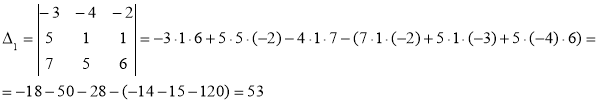
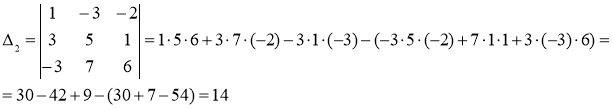
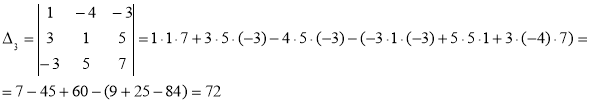
По формулам Крамера, имеем
![]()
![]()
![]()
б) 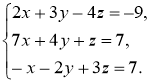
Рассмотрим матрицы
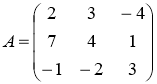
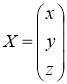
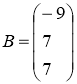
Тогда
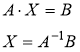
Найдем обратную к матрице А матрицу А-1 по формуле
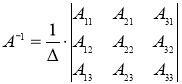
Вычислим определитель
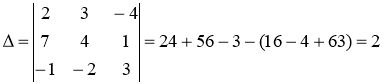
![]() Найдем алгебраические дополнения
Найдем алгебраические дополнения
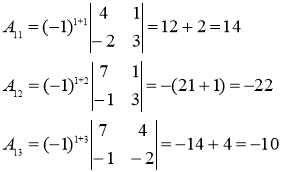
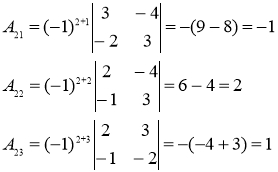
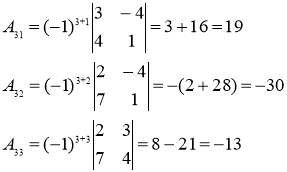
Обратная матрица
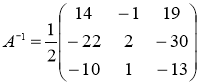
Находим 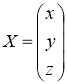
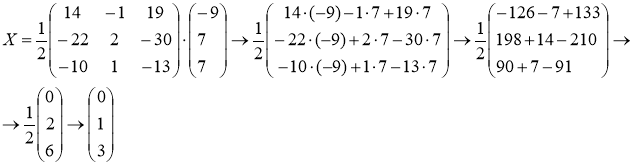
таким образом, ![]()
Ответ: а) ![]()
![]()
![]() , б)
, б) ![]()
Практическое занятие №4
№1 Доказать, что![]() (указать
(указать ![]() )
)
Решение.
По определению предела числовой последовательности ![]()
![]() ,
, ![]()
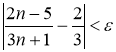 .
.
Будем решать последнее неравенство относительно ![]() :
: 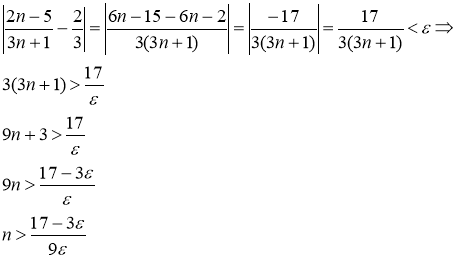
Таким образом, получили, что неравенство 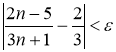 выполняется не для всех номеров
выполняется не для всех номеров ![]() , а только для тех, которые больше
, а только для тех, которые больше ![]() , следовательно, за
, следовательно, за ![]() можно взять целую часть числа
можно взять целую часть числа ![]() , то есть
, то есть 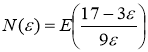 .
.
и тогда 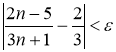 при
при ![]() .
.
Ответ: 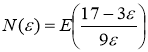
№2 Доказать(указать ![]() ), что
), что
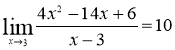
Решение.
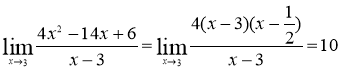
Пусть ![]() произвольное положительное число. Найдем такое число
произвольное положительное число. Найдем такое число ![]() (зависящее от
(зависящее от ![]() ), чтобы для всех
), чтобы для всех ![]() , удовлетворяющих неравенству
, удовлетворяющих неравенству ![]() , выполнялось неравенство
, выполнялось неравенство 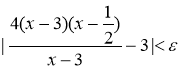 .
.
Преобразуем
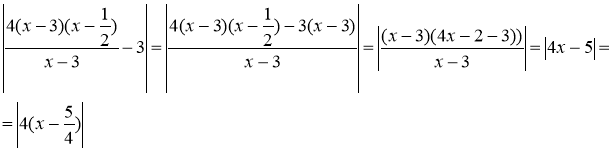 .
.
Используя неравенство ![]() , оценим
, оценим ![]() :
:
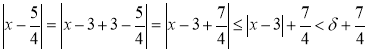
Следовательно, 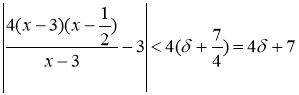 . Для выполнения неравенства
. Для выполнения неравенства 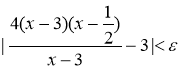 достаточно потребовать, чтобы
достаточно потребовать, чтобы ![]() то есть чтобы
то есть чтобы ![]() .
.
Ответ: ![]()
№3 Вычислить предел функции
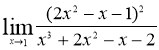
Решение.
Так как числитель и знаменатель обращается в нуль при ![]() , то 1 – корень обоих многочленов, а значит, каждый из них разлагается на множители, одним из которых будет
, то 1 – корень обоих многочленов, а значит, каждый из них разлагается на множители, одним из которых будет ![]() . Получаем
. Получаем
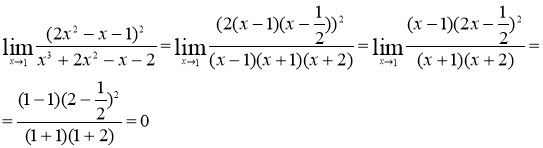
Ответ: 0
№4 Вычислить предел функции
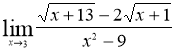
Решение.
Избавимся от иррациональности в числителе
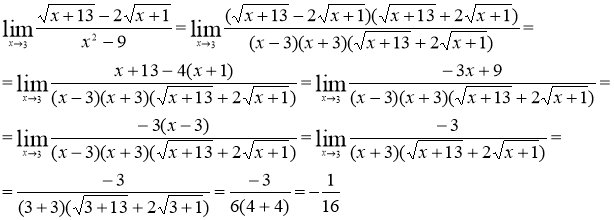
Ответ: ![]()
№5 Вычислить предел функции
![]()
Решение.
Используем первый замечательный предел 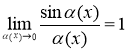 ,
,
формулу понижения степени ![]()
формулу ![]()
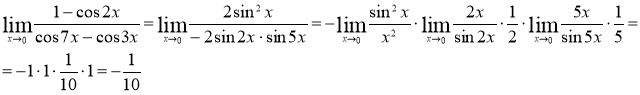 Ответ:
Ответ: ![]()
№6 Вычислить предел функции
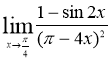
Решение.
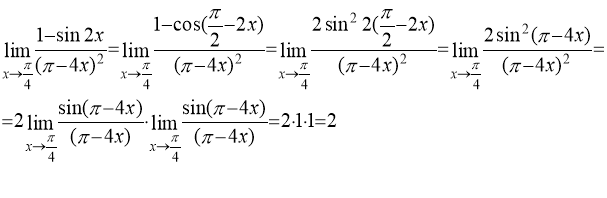
Ответ: 2
№7 Вычислить предел функции
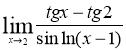
Решение.
Используем формулы
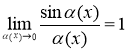
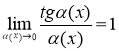
![]()
![]() , тогда
, тогда ![]()
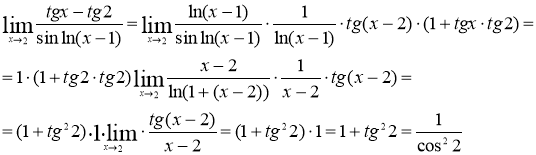
Ответ: ![]()
№8 Вычислить предел функции
![]()
Решение.
Так как ![]()
![]()
Тогда
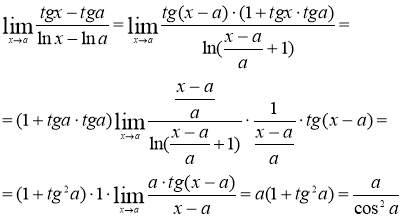
Ответ: ![]()
№9 Вычислить предел функции
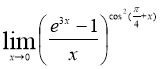
Решение.
Так как 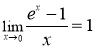 , то
, то
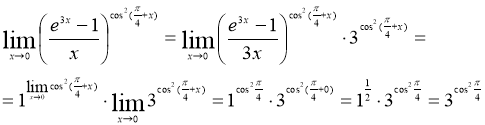
Ответ: ![]()
№10 Вычислить предел функции
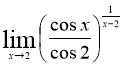
Решение.
Так как 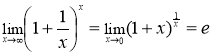 , то
, то
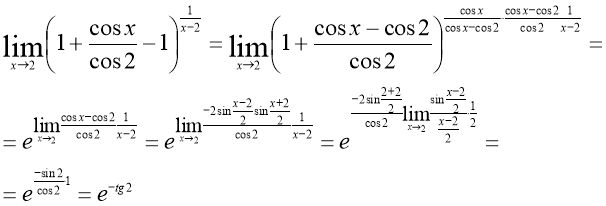
Ответ: ![]()
№11 Вычислить предел функции
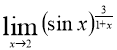
Решение.
Так как неопределенности нет, то
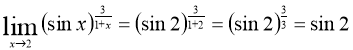
Ответ: ![]()
Практическая работа №5
№1 Найти производные функции
а) ![]()
б) 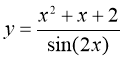
в) ![]()
Решение.
а) ![]()
Используем формулы
![]()
![]()
![]()
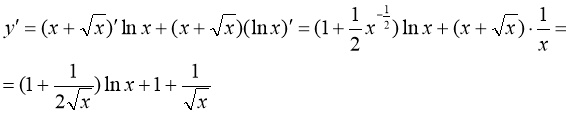
б) 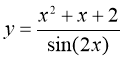
Используем формулы
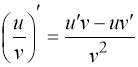 ,
, ![]()
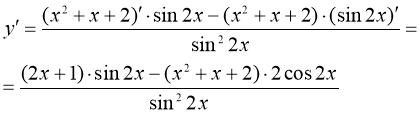
в) ![]()
Прологарифмируем данную функцию
![]()
Продифференцируем полученную функцию
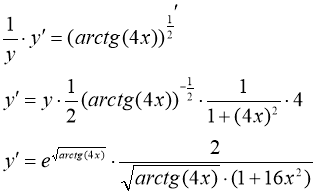
Использовали формулу
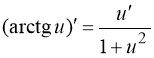
Ответ: а) 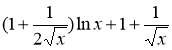 , б)
, б) 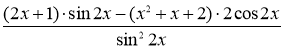 ,
,
в) 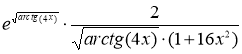
№2 Исследовать средствами дифференциального исчисления функцию. Найти асимптоты и построить график
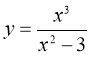
Решение.
Решение.
- Функция
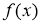 определена, если
определена, если
![]()
значит область определения ![]() .
.
- Найдем нули функции
Если х=0, то 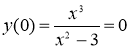
график пересекает ось ОY в точке (0;0)
Если у=0,то
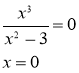
график пересекает ось Ох в точке (0;0)
- Выясним, является ли функция четной или нечетной. Находим
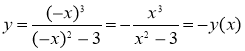
Функция является нечетной
- Данная функция не является периодической, так как значение функции изменится при добавлении к аргументу определенного, не равного нулю числа.
- Находим промежутки монотонности и точки экстремума функции.
Производная
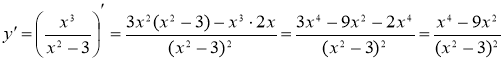
определена на ![]()
Для нахождения критических точек, решаем уравнение ![]()
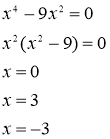
Получили критические точки ![]() ,
,![]() ,
, ![]() .
.
Так как ![]() при
при ![]() , то на интервалах
, то на интервалах ![]() функция возрастает,
функция возрастает,
![]() при
при ![]() , то на интервалах
, то на интервалах ![]() функция убывает.
функция убывает.
При x=-3 функция имеет максимум, т.к. переходе через эту точку ![]() меняет знак с «+» на «
меняет знак с «+» на «![]() ».
».
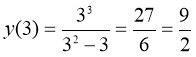 , значит точка
, значит точка ![]() - точка максимума
- точка максимума
При ![]() функция имеет минимум, т.к. переходе через эту точку
функция имеет минимум, т.к. переходе через эту точку ![]() меняет знак с «-» на «+».
меняет знак с «-» на «+».
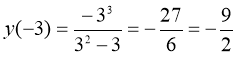 , значит точка
, значит точка ![]() - точка минимума
- точка минимума
- Определим интервалы выпуклости и вогнутости графика функции и точки перегиба.
Находим вторую производную
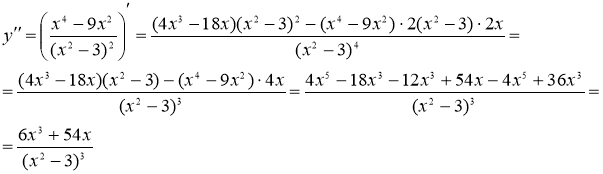
Она определена для ![]() .
.
![]() , при
, при
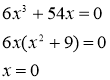
Так как ![]() при
при ![]() , то функция выпукла на интервалах
, то функция выпукла на интервалах ![]() ;
;
![]() при
при ![]() , то функция вогнута на
, то функция вогнута на ![]() .
.
Точка x = 0 – точка перегиба, так как при переходе через эту точку производная ![]() меняет знак.
меняет знак.
![]()
- Определим вертикальные, горизонтальные и наклонные асимптоты графика функции.
Функция является непрерывной во всех точках области определения. В точках ![]() ,
, ![]() функция имеет разрыв.
функция имеет разрыв.
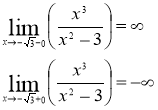
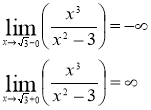
Значит в точках ![]() ,
, ![]() функция имеет разрыв 2-го рода
функция имеет разрыв 2-го рода
А прямые ![]() - вертикальные асимптоты.
- вертикальные асимптоты.
Найдём наклонные асимптоты ![]() , где
, где
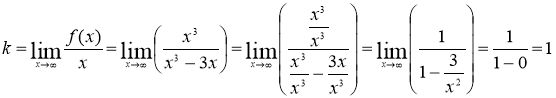
![]() Следовательно, y = x- уравнение наклонной асимптоты
Следовательно, y = x- уравнение наклонной асимптоты
График функции
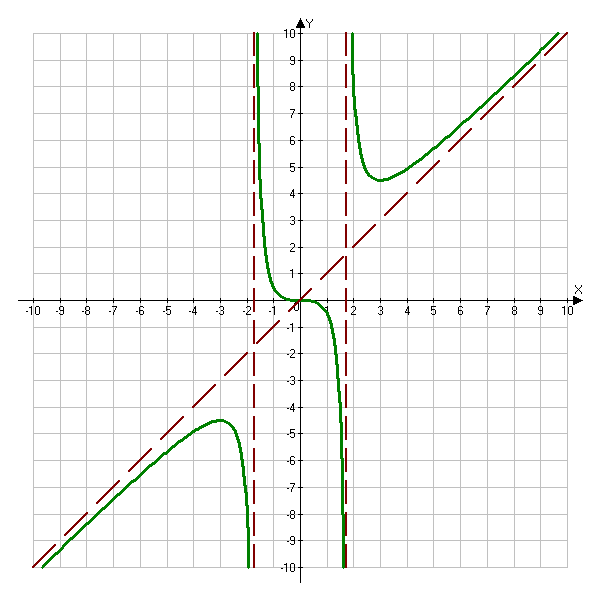
1
Имя файла: Mat12.doc
Размер файла: 483 Kb
Если закачивание файла не начнется через 10 сек, кликните по этой ссылке
