ДОМАШНЕЕ ЗАДАНИЕ К ТЕМЕ 10

ВАРИАНТ 1

 

Выбрать регулятор (закон регулирования) для статического объекта, передаточная функция которого приведена ниже.

 

Дано:

;

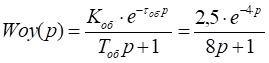·        Максимально-допустимое значение динамического отклонения регулируемой величины ε_max = 9 %;

·        Принятый типовой переходный процесс – апериодический переходный процесс;

·        Максимально-возможное значение возмущения на объект, выраженное в % хода регулирующего органа Δх_вх = 4%.

·        Допустимое остаточное отклонение, т.е. статическая ошибка, ε_ст = 5%

·        Допустимое время регулирования Тр = 20 сек.

 

Для упрощения расчетов и исследования характеристик САУ используем рекомендованный пакет прикладных программ Control System Toolbox, который является приложением системы MatLab и ориентирован на решение задач по теории автоматического управления.

Для использования функций Control System Toolbox в первую очередь следует ввести в среду MatLab все полученные ПФ. Наиболее удобно это делать в так называемой tf –форме.

Для создания tf-модели данной ПФ используется функция с одноименным идентификатором

H=tf ( [b_m, b_m-1, …, b₀],[a_n, a_n-1,…,a₀] ),

где H – имя созданной ПФ, […] – массивы коэффициентов полиномов числителя и знаменателя ПФ.

%Создадим tf-модель объекта управления:

Wou=tf([2.5], [8 1],'inputdelay',4);

% Определим переходный процесс при максимально-возможном значение возмущения на объект, выраженное в % хода регулирующего органа Δх_вх = 4%.

step (0.04*Wou) ; grid on

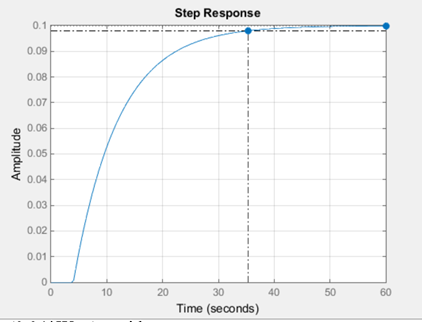
Рис. 1. Переходный процесс исходного объекта.

 

 

 

% Определим качество переходного процесса

stepinfo(0.04*Wou)

ans =

RiseTime: 17.5778

SettlingTime: 35.2975

SettlingMin: 0.0901

SettlingMax: 0.1000

Overshoot: 0

Undershoot: 0

Peak: 0.1000

PeakTime: 80.6826

Переходный процесс удовлетворяет заданным критериям:

·        по максимально-допустимому значение динамического отклонения регулируемой величины ε_max = 9 %;

·        по типу переходного процесса – апериодический переходный процесс;

·        по допустимому остаточному отклонению, т.е. статическая ошибка, ε_ст = 0%.

Но не удовлетворяет по допустимому времени регулирования Тр = 20 сек., которое равно  35,2975 с.

Введем корректирующее форсирующее звено и подберем его параметры.

Wkor= tf([7 1], [0 1]);

W=Wou*Wkor;

%W=feedback(Wou, Wpi)                         

step (0.04*W) ; grid on

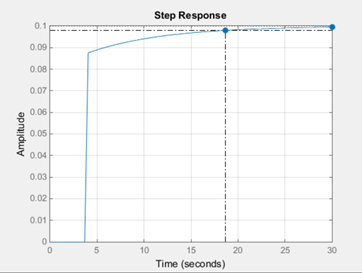
Рис. 2. Переходный процесс скорректированного объекта.

% Определим качество переходного процесса

stepinfo(0.04*W)

ans =

RiseTime: 2.0607

SettlingTime: 18.6626

SettlingMin: 0.0901

SettlingMax: 0.1000

Overshoot: 0

Undershoot: 0

Peak: 0.1000

Таким образом, время переходного процесса уменьшилось до 18.6626 с, что соответствует заданным требованиям.