Интегралы, дифференциальные уравнения, ряды -примеры решения.
Ниже приведены условия и решения задач. Закачка решений в формате doc начнется автоматически через 10 секунд.
№1 Найти неопределенные интегралы
а) 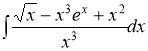 , б)
, б) ![]() , в)
, в) ![]() , г)
, г) 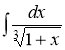
Решение.
а)
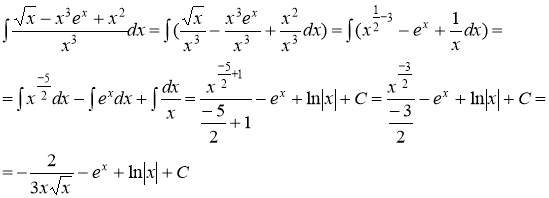
При вычислении использовали табличные интегралы
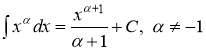 ,
, ![]() ,
, ![]()
б) ![]()
Используем теорему о «замене типа подведение под знак дифференциала»
![]() , где t = g(x)
, где t = g(x)
В данном случае ![]() . Тогда
. Тогда
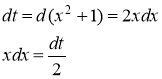
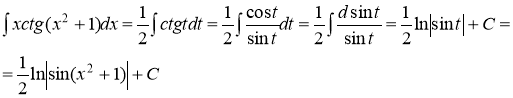
в) ![]()
Для вычисления данного интеграла будем использовать формулу интегрирования по частям![]()
Обозначим: ![]() ,
, ![]() . Тогда
. Тогда
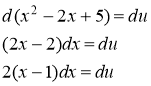
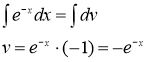
В итоге получим
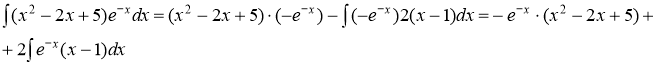
Интеграл ![]() также вычислим при помощи формулы интегрирования по частям
также вычислим при помощи формулы интегрирования по частям
Обозначим: ![]() ,
, ![]() . Тогда
. Тогда
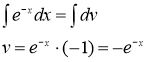
В итоге получим
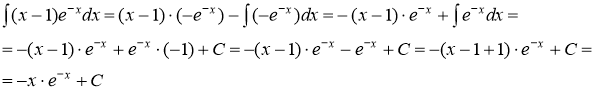
Тогда
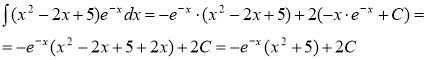
г) 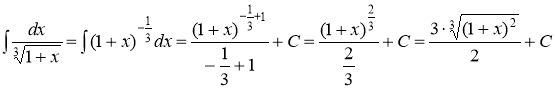
Ответ: а) 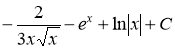 , б)
, б) ![]() ,в)
,в) ![]() ,
,
г) 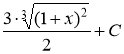
№2 Вычислить определенные интегралы
а) 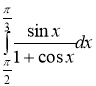 , б)
, б) 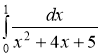 , в)
, в) 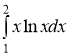 , г)
, г) 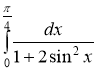
Решение.
а) 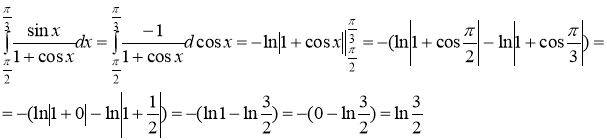
б)
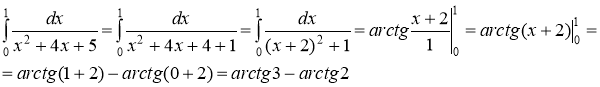
При вычислении использовали табличный интеграл
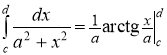
в) 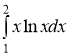
Используем метод интегрирования по частям:
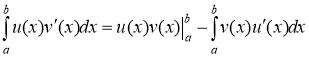
Обозначим: ![]() ,
, ![]() . Найдем v
. Найдем v
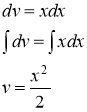
Найдем ![]() :
: ![]()
Тогда
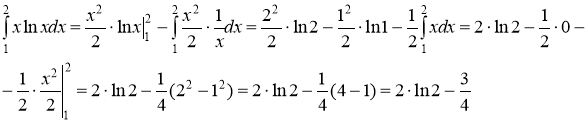
г) 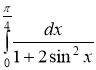
Применяем подстановку![]() , тогда
, тогда 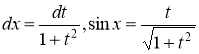
При x=0 ![]()
При x= ![]()
![]()
Переходя к новой переменной, получаем
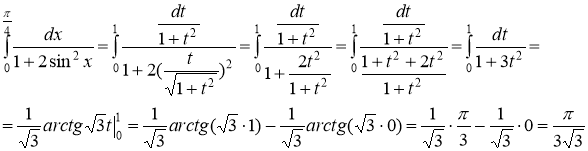
Ответ: а) ![]() , б)
, б) ![]() , в)
, в) ![]() , г)
, г) ![]()
№3 Найти общие решения дифференциальных уравнений
а) ![]() , б)
, б) ![]()
Решение.
а) ![]()
Данное уравнение является уравнением с разделяющими переменными.
Постараемся преобразовать уравнение так, чтобы в левой его части было выражение, содержащее только переменную y, а в правой неизвестную функцию x.
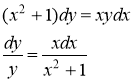
Равенство дифференциалов предполагает, что сами функции отличаются друг от друга на некоторую константу С, т.е.
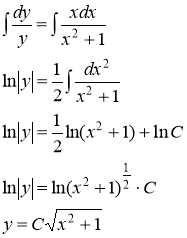
б) ![]()
Данное уравнение является уравнением с разделяющими переменными.
![]()
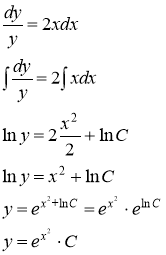
Ответ: а) ![]() , б)
, б) ![]()
№4 Решить линейное неоднородное дифференциальное уравнение
![]()
Решение.
Разделим уравнение на ![]()
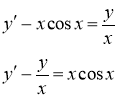
Данное уравнение является линейным.
Сделаем подстановку ![]() , где
, где ![]() - неизвестные функции от х. Тогда
- неизвестные функции от х. Тогда ![]() . Подставляя выражения
. Подставляя выражения ![]() и
и ![]() в данное уравнение, получаем:
в данное уравнение, получаем:
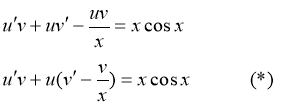
Подберем функцию ![]() так, чтобы выражение в скобках было равно нулю, т.е. решим диф. уравнение
так, чтобы выражение в скобках было равно нулю, т.е. решим диф. уравнение ![]() . Итак,
. Итак,
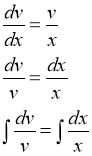
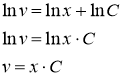
Ввиду свободы выбора функции ![]() , можно принять с=1. Отсюда
, можно принять с=1. Отсюда ![]() Подставляя найденную функцию
Подставляя найденную функцию ![]() в уравнение (*), получаем:
в уравнение (*), получаем:
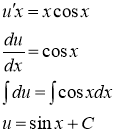
Возвращаясь к переменной ![]() , получаем решение
, получаем решение
![]()
Ответ: ![]()
№5 Найти решение задачи Коши
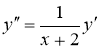 ,
, ![]()
Решение.
Данное уравнение является уравнением, допускающим понижение порядка.
Полагаем ![]() , получим
, получим ![]() . Подставим данные выражения в исходное уравнение
. Подставим данные выражения в исходное уравнение
![]()
Данное уравнение является уравнением с разделяющимися переменными. Разделяем переменные
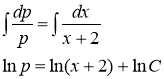
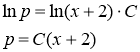
Заменяя вспомогательную переменную р через ![]() , получим уравнение
, получим уравнение
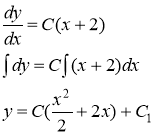
Чтобы найти указанное частное решение, подставим начальные данные ![]() в полученное выражение
в полученное выражение
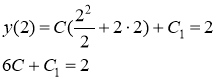
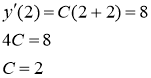
Тогда
![]()
Таким образом, частное решение имеет вид
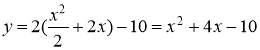
Ответ: ![]()
№6 Решить уранение
![]()
Решение.
Найдем сначала общее решение соответствующего однородного уравнения ![]()
Составим характеристическое уравнение ![]() . Решаем его:
. Решаем его:
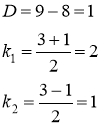
Тогда общее решение исходного уравнения есть
![]() .
.
Переходим к отысканию частного решения исходного уравнения. В данном случае частное решение ищем в виде
![]()
Найдем производные данной функции
![]()
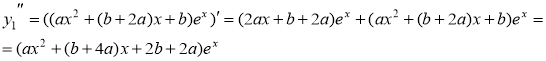
Подставим данные выражения в исходное уравнение, получаем
![]()
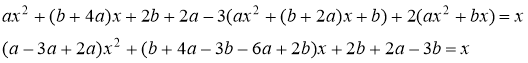
![]()
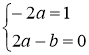
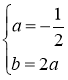
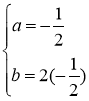
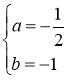
Следовательно, частное решение имеет вид
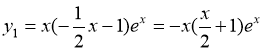
Общее решение имеет вид
![]()
Ответ: ![]()
№7 Исследовать на сходимость ряд 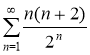
Решение.
Воспользуемся признаком Даламбера.
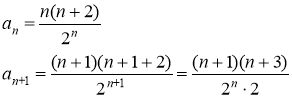
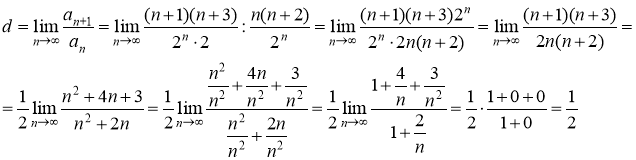
Так как ![]() то ряд
то ряд 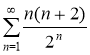 - сходится.
- сходится.
Ответ: ряд сходится по признаку Даламбера
№8 Найти области сходимости степенных рядов:
а) 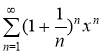 , б)
, б) 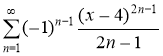
Решение.
а) 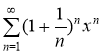
Найдем радиус сходимости по формуле
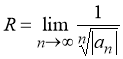
Где ![]()
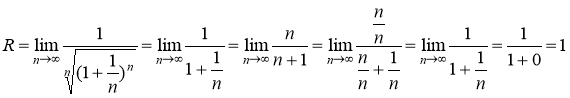
то есть ряд сходится при ![]() , отсюда границы интервала сходимости
, отсюда границы интервала сходимости ![]()
Исследуем отдельно точки ![]()
При х = ![]() имеем ряд
имеем ряд 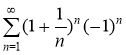
Это знакочередующийся ряд, для которого не выполнены условия признака Лейбница:
Общий член ряда не стремится к нулю:
![]()
При х =1 имеем ряд 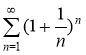
Данный ряд расходится, так как не выполнено необходимое условие сходимости рядов
![]()
Следовательно, областью сходимости исходного ряда является интервал ![]()
б) 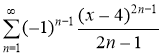
Интервал сходимости находим из следующего условия:
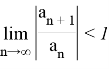
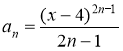
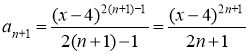
Тогда
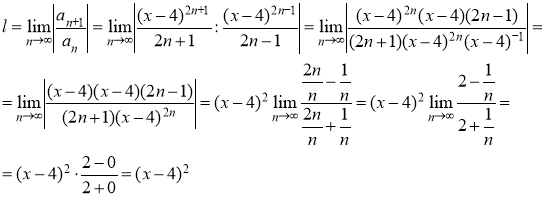
Следовательно, ряд сходится при
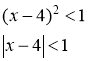
![]() .
.
Исследуем сходимость ряда на концах этого интервала.
При х =3 имеем ряд
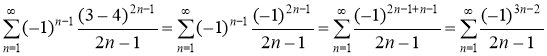
Это знакочередующийся ряд, для которого выполнены условия признака Лейбница:
1) Общий член ряда стремится к нулю:
![]()
2) Последовательность абсолютных величин членов ряда монотонно убывает:
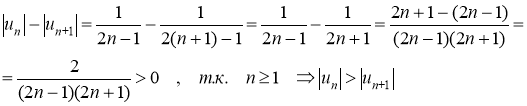
Следовательно ряд 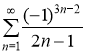 сходится условно по признаку Лейбница.
сходится условно по признаку Лейбница.
При х =5 имеем ряд
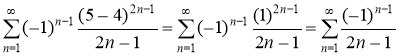
Это знакочередующийся ряд, для которого выполнены условия признака Лейбница.
Следовательно, областью сходимости исходного ряда является отрезок [3,5].
Ответ: а) ![]() , б) [3,5].
, б) [3,5].
№9 Разложить функцию ![]() в ряд Маклорена и указать область сходимости полученного ряда.
в ряд Маклорена и указать область сходимости полученного ряда.
Решение.
Разложим функцию ![]() в ряд, для чего воспользуемся формулой
в ряд, для чего воспользуемся формулой
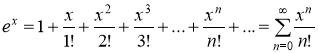
заменив в этой формуле x на ![]() . Получим:
. Получим:
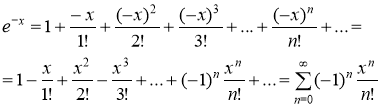
Разложение функции ![]() имеет вид
имеет вид

Определим область сходимости. Поскольку разложение экспоненты ![]()
сходится при любом х, то область сходимости полученного ряда: ![]()
Ответ: 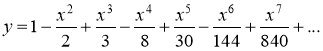 ,
, ![]()
1
Имя файла: Mat6.doc
Размер файла: 403 Kb
Если закачивание файла не начнется через 10 сек, кликните по этой ссылке
