Функции нескольких переменных - производные, экстремум.

№1.8. Найти частные производные второго порядка функции

Решение.

Найдем частные производные первого порядка

При нахождении будем считать y постоянным

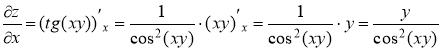
При нахождении будем считать х постоянным

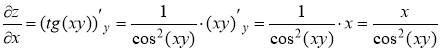
Найдем частные производные второго порядка

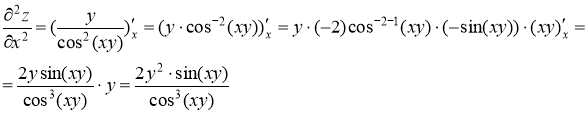
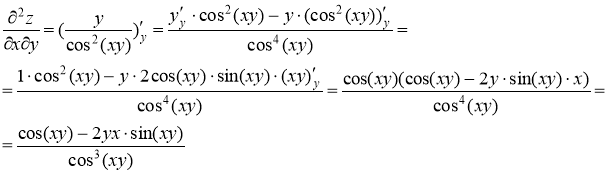
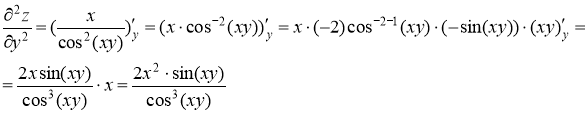
Ответ: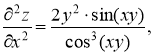   

 

 

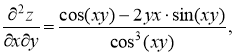
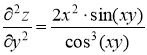
№2.8. Найти экстремум  функции двух переменных

Решение.

Находим первые частные производные данной функции:

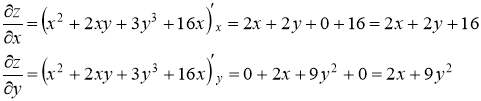
Приравнивая их к нулю, получаем систему уравнений

  

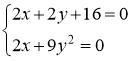
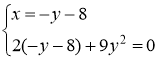
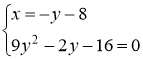
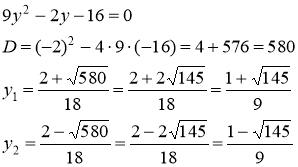
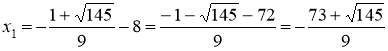
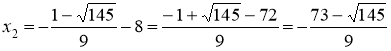
Получили стационарные точки данной функции:  ,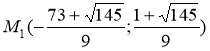

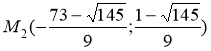
Вычислим вторые частные производные:

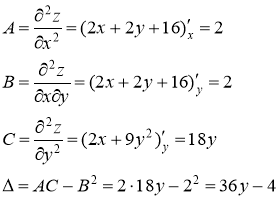
Для точки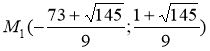

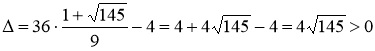и , то в точке 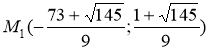функция имеет минимум.

Для точки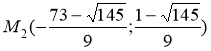

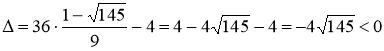
Значит, в этой точке экстремума нет.

Ответ: 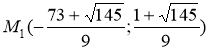- точка минимума

 

№3.8. Найти экстремум  функции

Решение.

Находим первые частные производные данной функции:

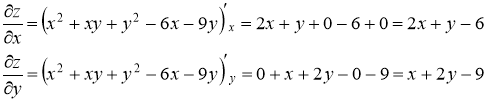
Приравнивая их к нулю, получаем систему уравнений

      

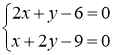
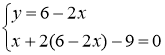
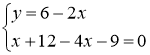
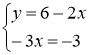
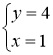
Получили стационарную точку данной функции: 

Вычислим вторые частные производные:

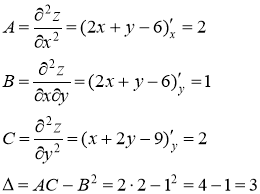
Так как и , то в точке функция имеет минимум.

Ответ: - точка минимума