Дифференциальные уравнения.

Вариант №8

№1

Решение.

Данное уравнение является уравнением, приводящееся к однородному. Разделим уравнение на

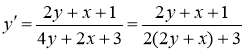
Решаем его с помощью подстановки

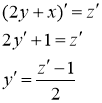
Получили уравнение с разделяющимися переменными. Разделяем переменные

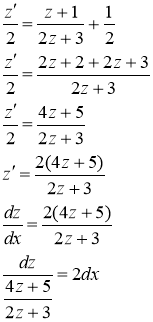
Интегрируем обе части последнего равенства

 

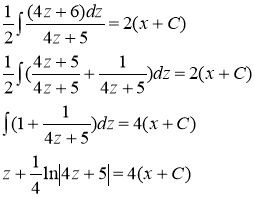
Так как , то получаем общий интеграл данного дифференциального уравнения.

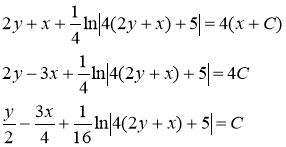
Ответ:

 

 

№2

Решение.

Разделим на

Разделим на

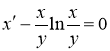
Данное уравнение является однородным уравнением. Решаем его с помощью подстановки . Находим:

Подставляем в уравнение.

Получили уравнение с разделяющимися переменными. Разделяем переменные

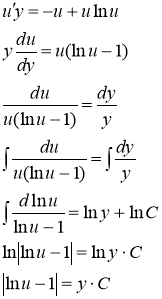
  Так как ,то получаем общий интеграл данного дифф. уравнения.

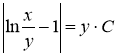
Ответ: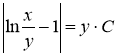

 

 

 

 

 

№3

Решение.

Данное уравнение является уравнением с разделяющими переменными.

  Постараемся преобразовать уравнение так, чтобы в левой его части было выражение, содержащее только переменную y, а в правой неизвестную функцию x.

 Разделим на

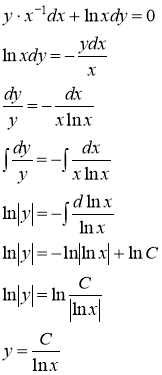
Ответ:

 

№4

Решение.

Данное уравнение является линейным.

Сделаем подстановку  , где - неизвестные функции   от х. Тогда . Подставляя выражения и в данное уравнение, получаем:

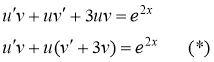
Подберем функцию так, чтобы выражение в скобках было равно нулю, т.е. решим диф. уравнение  . Итак,

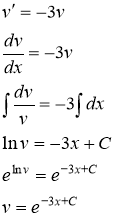
Ввиду свободы выбора функции , можно принять с=0. Отсюда   Подставляя найденную функцию в уравнение (*), получаем:

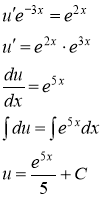
Возвращаясь к переменной , получаем решение

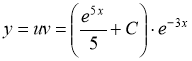
Ответ: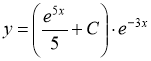

 

 

 

№5

Решение.

Данное уравнение является уравнением Бернулли

Сделаем подстановку  , где - неизвестные функции   от х. Тогда . Подставляя выражения и в данное уравнение, получаем:

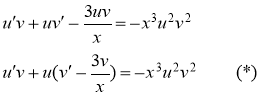
Подберем функцию так, чтобы выражение в скобках было равно нулю, т.е. решим диф. уравнение  . Итак,

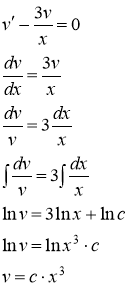
Ввиду свободы выбора функции , можно принять с=1. Отсюда   Подставляя найденную функцию в уравнение (*), получаем:

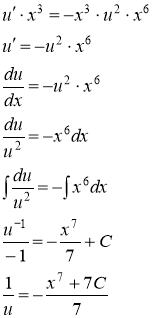
Возвращаясь к переменной , получаем решение

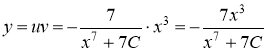
Ответ: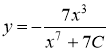

 

№6

Решение.

Данное уравнение является уравнением, допускающим понижение порядка.

Полагаем , получим . Подставим данные выражения в исходное уравнение

Данное уравнение является линейным.

Сделаем подстановку  , где - неизвестные функции   от х. Тогда . Подставляя выражения и в данное уравнение, получаем:

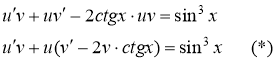
Подберем функцию так, чтобы выражение в скобках было равно нулю, т.е. решим диф. уравнение  . Итак,

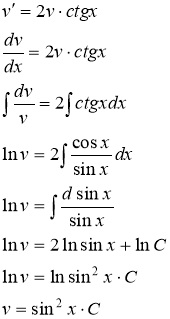
Ввиду свободы выбора функции , можно принять с=0. Отсюда   Подставляя найденную функцию в уравнение (*), получаем:

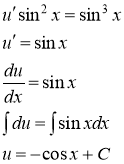
Возвращаясь к переменной , получаем решение

Та как , то

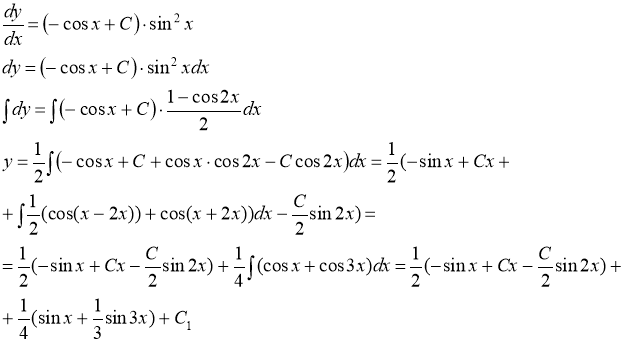
Ответ:

 

№7

Решение.

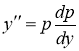 Это неполное уравнение 2-го порядка, не содержащее явно аргумента x. Положим , тогда. Подставим данные выражения в исходное уравнение

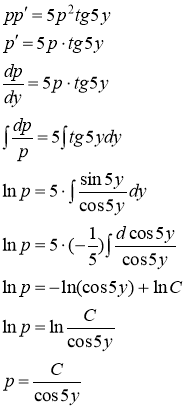
Заменяя вспомогательную переменную р через , получим уравнение

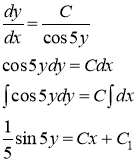
Ответ:

 

№8

Решение.

Найдем сначала общее решение соответствующего однородного уравнения

Составим характеристическое уравнение . Решаем его:

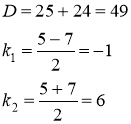
Тогда общее решение исходного уравнения есть .

 Переходим к отысканию частного решения исходного уравнения. В данном случае частное решение ищем в виде

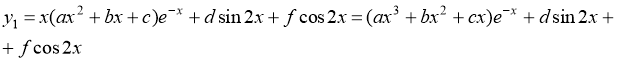
           Найдем производные данной функции

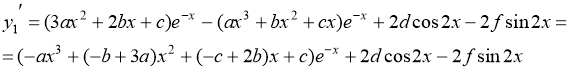
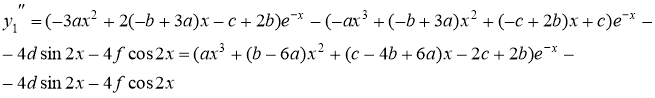
 Подставим данные выражения в исходное уравнение, получаем

 

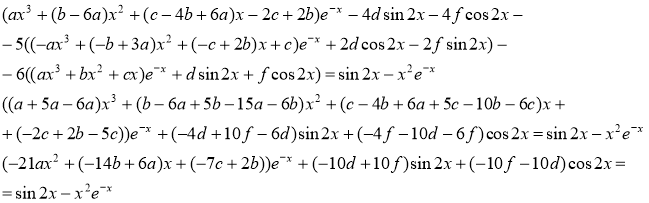
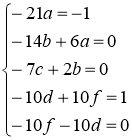
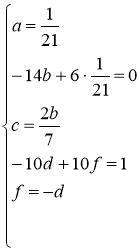
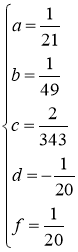
        Следовательно, частное решение имеет вид

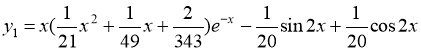
 Общее решение имеет вид

Ответ:

 

 

 

№ 9

Решение.

Решим данное  линейное неоднородное дифференциальное уравнение второго порядка методом Лагранжа.

Найдем сначала общее решение соответствующего однородного уравнения

Составим характеристическое уравнение. Решаем его:

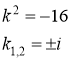
Тогда общее решение исходного уравнения есть

 Составляем систему уравнений:

,  

 

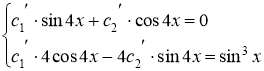
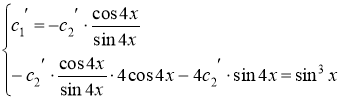
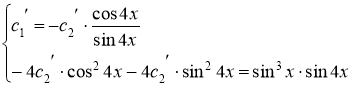
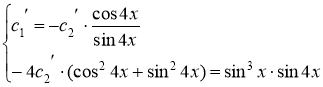
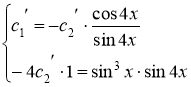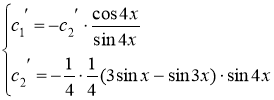
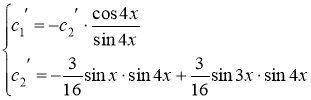
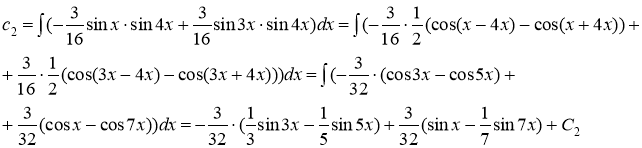
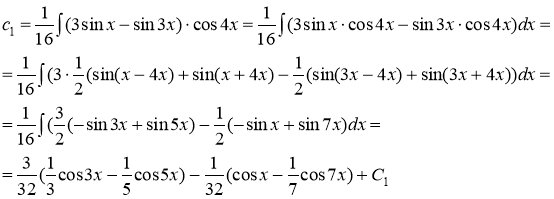
 Подставляем полученные значения в формулу общего решения неоднородного уравнения.

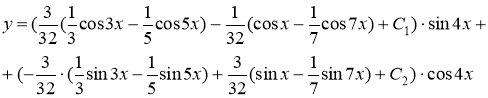
Ответ: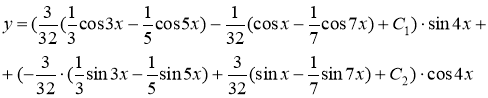

 

 

№10 ,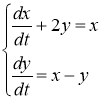

Решение.

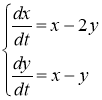
Решим систему классическим методом

Дифференцируя по t первое уравнение системы и используя данные уравнения, находим

Выразим из первого уравнения . Тогда

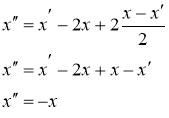
Получили уравнение

Получили уравнение второго порядка с постоянными коэффициентами. Составим характеристическое уравнение . Решаем его:

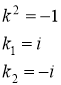
 Следовательно, общее решение определяется формулой

.

Поскольку и

то

 

Следовательно, общее решение данной системы определяется формулами

,

Найдем частное решение системы, для этого подставим начальное условие в полученное решение.

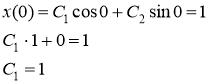
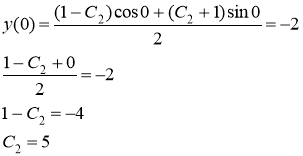
Искомое частное решение примет вид

,

Ответ: ,