Примеры решенных задач по гидравлике - 6

Задача № 1

Определить величину абсолютного и вакуумметрического давлений на поверхности воды в резервуаре при Н=l,2м, если известна высота подъема ртути h=20см. Плотность ртути 13600 кг/м3, плотность воды 1000кг/м3, атмосферное давление принять равным 100 кПа.

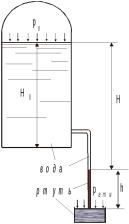
Рисунок 1

 

Решение:

Перевод в СИ

h=20см =0,2м

Согласно основному уравнению статики:

Абсолютное давление на поверхности воды:

Па=61,55кПа

кг/м3 – плотность воды;

кг/м3 – плотность воды;

м – высота столба воды;

м – высота столба ртути;

м/с2 – ускорение свободного падения.

Вакууметрическое давление на поверхности воды:

Па=38,45кПа

 

Задача 2

Трапецеидальной канал в суглинке имеет ширину по дну b = 5,5 м, глубину h = 1,8 м, заложение откосов m = 1 и уклон i = 0,0004.

Определить расход при равномерном движении воды.

Решение

Расход через определяется по формуле:

где скорость в канале;

площадь живого сечения канала равна

Площадь живого сечения канала определится по формуле:

м2

Смоченный периметр:

м

Гидравлический радиус для канала равен

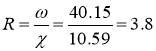
Коэффициент Шези по формуле Маннинга:

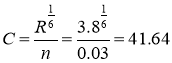
n =0,03 коэффициент шеро­ховатости

Скорость в канале определится по формуле:

м/с

Расход:

м3/с

 

 

 

 

 

Задача 3

Вода вытекает из бассейна шириной B = 2 м и глубиной Н1 = 3 м в ло-ток шириной b = 0,15 м и глубиной h2 = 0,25 м через круглое отверстие в тонкой стенке диаметром d = 0,1 м с центром расположения на расстоянии а = 0,1 м от дна. Определить расход воды Q через отверстие.

 

Решение:

Расход через отверстие определяется по формуле:

В случае полного, но несовершенного сжатия коэффициент расхода будет также больше коэффициента расхода для полного, и совершенного сжатия. Зависимость между этими коэффициентами можно представить эмпирической формулой:

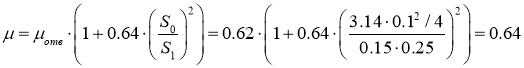
где коэффициент расхода отверстия

площадь сечения

м – напор над отверстием.

м3/с=38л/с

 

Задача 4

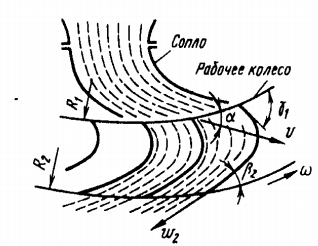
Рабочее колесо активной центробежной турбины имеет радиусы входной и выходной R1 = 1,25 м и R2 = 1,5 м. Струя воды поступает на колесо со скоростью v = 60 м/с под средним углом к входной окружности 1 = 250; число оборотов колеса n = 250 об/мин.

Коэффициент сопротивления колеса, выражающий потерю напора через относительную скорость выхода из колеса равен ζ = 25.

Определить:

1) Входной угол лопастей γ1, при котором натекание на них струи будет безударным.

2) Момент, развиваемый потоком на рабочем колесе, если выходной угол лопастей β2 = 150 и расход воды Q = 160 л/с.

Решение

Определим угловую скорость колеса:

с-1

Из условий безударного входа из треугольника скоростей на входе:

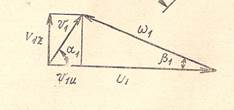
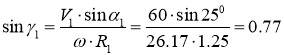
Согласно уравнению Бернулли:

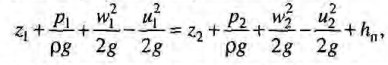
м/с

м/с

м/с

потери напора

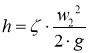
Подставляя получим

м/с

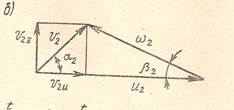
Определим скорость V2и:

м/с

Момент равен:

Нм

 

Задача  5

 

5.Насос с подачей Q=0,01м3/с забирает воду из колодца, сообщающегося с водоемом чугунной трубой диаметром d = 158 мм, длиной l=108 м (рис.1).

На входе во всасывающую трубу установлена сетка. Температура воды в водоеме 20 °С. Найти перепад уровней воды Δh в водоеме и в колодце.(рисунок прилагается)

 

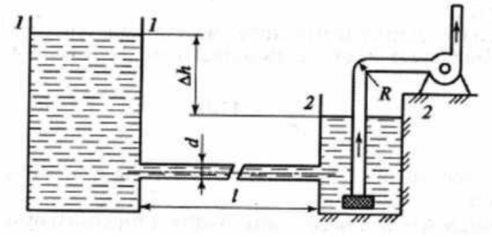
Решение:

 

Применим уравнение Бернулли для свободных поверхностей жидкости баков. Плоскость сравнения проведем через плоскость нижнего бака.

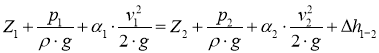
Пологая, что режим течения турбулентный, т. е. . Учитывая, что скорость на свободной поверхности равна 0 , а также и можно записать:

- потери напора;

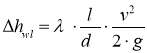потери напора по длине;

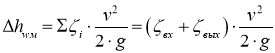местные потери напора;

где - коэф-т сопротивления входа.

- коэф-т сопротивления выхода.

Преобразуя, получим

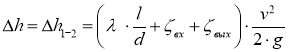
Определяем среднюю скорость в трубе:

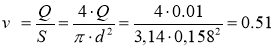м/с

Определим число Рейнольдса:

где м2/с кинематическая вязкость воды при 200С.

Т.к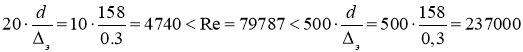

мм – коэффициент шероховатости трубы (чугунная новая труба).

Значение определяется по формуле Альштуля (переходная область):

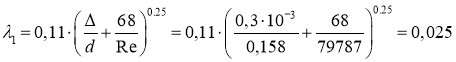
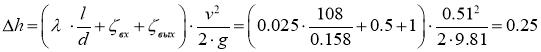м