Примеры решенных задач по гидравлике - 5

    Определить на какую высоту Δh поднимается уровень нефтепродукта в резервуаре диаметром D, глубиной наполнения H при увеличении температуры на Δt, если температурный коэффициент объёмного расширения нефтепродукта βt=0.00092°C-1.

    Дано : D=9.5 м ; H=12 м ; Δt=25°C ; βt=0.00092 1/°C.

    Найти : Δh

                                                                        Решение.

    Определим увеличение объёма нефтепродукта вследствие его нагрева на Δt по формуле

                              ΔV=βtVΔt                                            (1)

    где βt – коэффициент объёмного расширения ; V – первоначальный объём нефтепродукта.

    Первоначальный объём нефтепродукта :

                               V=                                           (2)

    где D – диаметр резервуара ; H – глубина наполнения.

    С учётом (2) формула (1) примет вид :

                               ΔV=                                  (3)

    С другой стороны, объём ΔV равен :

                               ΔV=                                            (4)

    где Δh – высота подъёма уровня нефтепродукта.

    Приравнивая правые части уравнений (3) и (4), получим :

                                

     Или, после сокращения на πD2/4, получим :

                                  Δh=βtHΔt                                            (5)

    Вычисления по формуле (5) дают :

                                  Δh=0.00092×12×25=0.276 м=276 мм.

    Ответ : Δh=276 мм.

 

                                                                         № 17.

    Определить предварительное поджатие пружины x, нагружающей дифференциальный предохранительный клапан, необходимое для того, чтобы клапан открывался при давлении p. Диаметры поршней D1, D2, а жёсткость пружины С.

    Дано : p=3.3 МПа ; D1=28 мм ; D2=26 мм ; C=9.5 Н/мм.

    Найти : x

                                                                  Решение.

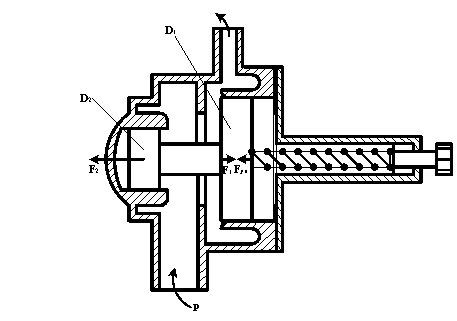
    На поршни клапана действуют следующие силы : на поршень диаметра D2 – сила давления F2 ; на поршень диаметра D1 – сила давления F1 и сила упругости Fуп пружины, приложенная к поршню диаметра D1.

    Величину предварительного поджатия x пружины определим из условия равновесия клапана :

                   F2+Fуп=F1                                           (1)

    Сила давления на поршень диаметра D2 равна :

                    F2=pS2=                                   (2)

    где p – давление в камере клапана ; S2 – площадь поршня диаметра D2.

    Сила давления на поршень диаметра D1 равна :

                    F1=pS1=                                   (3)

    Сила упругости пружины :

                     Fупр=Сx                                              (4)

    где C – коэффициент жёсткости пружины ; x – деформация пружины.

    Подставляя (2), (3) и (4) в (1), получим :

                     

    Отсюда находим величину x предварительного поджатия пружины :

                          x=                            (5)

    Вычисления по формуле (5) дают :

                          x= м=29 мм

    Ответ : x=29 мм.

                                                                          № 46.

    В баке А жидкость Ж  подогревается до температуры t°C и самотёком по трубопроводу длинной l1 попадает в производственный цех. Напор в баке А равен H. Каким должен быть диаметр трубопровода, чтобы обеспечивалась подача жидкости в количестве Q при манометрическом давлении в конце трубопровода не ниже pм? При расчёте принять, что местные потери напора составляют 20% от потерь по длине. Построить пьезометрическую и напорную линии.

    Дано : материал трубопровода – чугун старый ; Ж – керосин Т-1 ; Q=2.5 л/c ; t=80°C ; H=6.7 м ; l1=4.8 м ; pм=24 кПа ; hм=0.2hl.

    Найти : d.

                                                                   Решение.

    Выберем плоскость отсчёта на уровне плоскости совпадающей с линией центров тяжести сечений трубопровода. Тогда уравнение Бернулли для трёх сечений ( 1 – сечение на уровне свободной поверхности жидкости в баке А ; 2 – сечение в месте выхода трубопровода из бака А ; 3 – сечение в месте установки манометра М) :

                 H=    или для двух сечений 1 и 3

                 H=                                                (1)

    где H – напор в баке А ; pм – избыточное давление в сечении 3 ; ρ – плотность жидкости ; v – скорость движения жидкости в трубопроводе ; hм – потери напора в трубопроводе.

    Определим плотность жидкости при t=80°C по формуле :

                       ρ=                                                       (2)

     где ρ0=808 кг/м3 – плотность керосина при t0=20°C (табл. 1 [2]) ; α=0.0007 1/°C - коэффициент температурного расширения (табл. 1 [2]) ; Δt=t-t0=80-20=60°C.

    Вычисления по формуле (2) дают :

                        ρ= кг/м3

    Потери напора hw складываются из потерь hℓ по длине трубопровода и hм местных потерь :

                        hw=hℓ+hм                                                        (3)

    Потери по длине трубопровода определяются выражением :

                        hℓ=                                         (4)

    где Q – расход жидкости в трубопроводе ; l – длина трубопровода ; d – диаметр трубопровода ; λ – коэффициент гидравлического трения.

    Коэффициент гидравлического трения по формуле :

                         λ=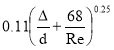                                       (5)

    где Δ=1.4 мм – эквивалентная шероховатость для чугунных старых труб (табл. [3]) ; Re – число Рейнольдса.

   Число Рейнольдса определим по формуле :

                                Re=                                                  (6)

    где ν=0.01×10-4 м2/с – кинематическая вязкость при t=80° (табл. 1 [2] найдено при помощи интерполяции).

    С учётом (6) формула (5) примет вид :

                          λ=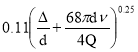                                  (7)

    Подставляя, полученное выражение для λ согласно (7) в (4), получим :

           hℓ=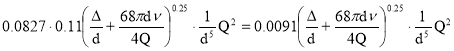       (8)

    Согласно условия местные потери :

                                    hм=0.2hℓ                                                 (9)

    С учётом (8) и (9) формула (3) примет вид :

        hw=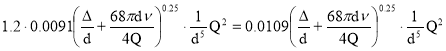            (10)

     Подставляя (10) в (1) и, учитывая выражение для скорости v, получим :

                H=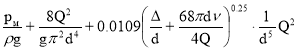                         (11)

    Подставляя в (11) заданные числовые значения, получим :          

          Н=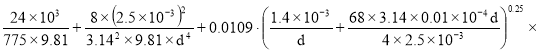

        

    H=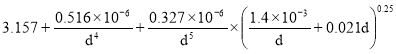                       (12)

    Для определения диаметра трубопровода построим зависимость H=f(d) согласно выражения (12). Для построения зависимости H=f(d) составим таблицу :

H, м	10.1	6.3	4.7	4	3.7
d, мм	30	35	40	45	50

    По результатам расчета построена зависимость H=f(d). На этом же рисунке построена прямая Hг=6.7 м.

    Пересечение кривой H=f(d) и прямой H=6.7 м даёт точку А. По графику определяем значение диаметра трубопровода : d=35 мм.

    Построим пьезометрическую и напорную линии, при d=50 мм.

    По формуле (10) вычисляем потери напора в трубопроводе :

         hw=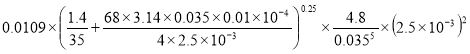=2.8 м

    Пьезометрическая высота в сечении 3 :

                    hp3= м

    Полный напор в сечении 3 :

        h3=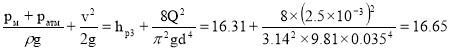 м

    Пьезометрическая высота в сечении 2 :

                     hp2= м

    Полный напор в сечении 2 :

                 h2=hp2=19.85 м.

    На основании вычислений строим пьезометрическую и напорную линию.

    Ответ : d=35 мм.

 

 

 

 

 

 

                                                                          № 50.

    Определить длину трубы l, при которой расход жидкости из бака будет в два раза меньше, чем через отверстие того же диаметра d. Напор над отверстием равен H. Коэффициент гидравлического трения в трубе принять равным λ=0.025.

    Дано : H=8 м ; d=60 мм ; Q1=0.5Q2 ; λ=0.025.

    Найти : l.

                                                                    Решение.

    Составим уравнение Бернулли для двух сечений трубы 0-0 и 1-1 :

                             H=                                                   (1)

    где v1 – скорость в сечении 1-1 ; hλ – потери напора по длине тубы.

    Потери напора определяются по формуле Вейсбаха-Дарси :

                               hλ=              (2)

    где λ – коэффициент гидравлического трения ; Q1 расход в трубе.

    Подставляя (2) в (1) и, учитывая что скорость v1 связана с расходом Q1 выражением :

                               v1=, получим:

                               H=

    Отсюда находим длину трубы :

                          l=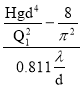                                             (3)

    Расход через отверстие определяется выражением :

                               Q2=                                         (4)

    где μ=0.62 – коэффициент расхода (рекомендации стр. 109 [1]) ; S0 – площадь сечения отверстия (S0=πd2/4) ; H – напор, под которым происходит истечение (глубина погружения отверстия под уровень жидкости в баке).

    Учитывая, что по условию Q1=0.5Q2, то подставляя (4) в (3) и, учитывая выражение для S0, получим :

                             l=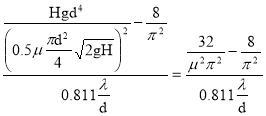           (5)

    Вычисления по формуле (5) дают :

                              l=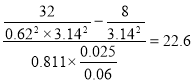 м

    Ответ : l=22.6 м

 

 

 

                                                                          № 63.

    Центробежный насос, подающий воду из бака А в бак B на высоту Hг, снабжён обводной трубой, по которой часть его подачи возрастает на сторону всасывания. Диаметр всасывающей и нагнетательной труб d, их общая расчётная длина L=l1+l2, коэффициент гидравлического трения λ=0.025. Диаметр обводной трубы d0, её суммарный коэффициент сопротивления ζ=25.

    С учётом заданной характеристики насоса определить подачу в верхний бак, напор насоса и потребляемую им мощность. Какова будет потребляемая насосом мощность, если такую же подачу в верхний бак осуществлять при выключенной обводной трубе путём перекрытия задвижки на линии нагнетания?

    Дано : Hг=35 м ; d=105 мм ; L=240 м ; d0=50 мм.

    Найти : Q, H, N.

                                                                    Решение.

    Напор, развиваемый насосом, расходуется на подъём воды на геометрическую высоту Hг и преодоление потерь напора во всасывающей, нагнетательной и обводной линиях  :

                            Hн=Hг+h1+h2                                                         (1)

    Потери напора состоят из потерь напора по длине во всасывающей и нагнетательной линиях и в местных сопротивлениях обводной линии.                     

    Потери напора по длине определим по формуле Вейсбаха-Дарси :

                                   h1=                                                   (2)                                 

    где λ – гидравлический коэффициент трения ; L – общая расчётная длина всасывающей и нагнетательной линий ; d – диаметр труб всасывающей и нагнетательной линий ; v1 - скорость движения жидкости во всасывающей и нагнетательной линиях.

    Скорость движения  воды во всасывающей и нагнетательной линиях :

                                  v1=                                                  (3)

    где S – площадь сечения труб всасывающей и нагнетательной линий.

    С учётом (3) формула (2) примет вид :

                                  h1=                      (4) 

    Потери напора в местных сопротивлениях обводной линии по формуле Вейсбаха :

                                  h2=                                                          (5)

    где ζ – суммарный коэффициент сопротивления обводной линии ; v2 – скорость движения жидкости в обводной линии.

    Скорость движения воды в обводной линии :

                                   v2=                                                (6)

    S0 – площадь сечения труб обводной линии ; d0 – диаметр труб обводной линии.

    С учётом (6) формула (5) примет вид :

                                 h2=                                 (7)

    С учётом (4) и (7) формула (1) примет вид :

                                 Hн=                       (8)

    где Q1 – расход во всасывающей и нагнетательной линии ; Q2 – расход в обводной линии.

    Расходы Q1 и Q2 определим следующим образом. Скорость потока в точке D определим двумя способами :

                     vD=Q1/S   ;    vD=Q2/S0  ;    ;  Q1=

    Расход через насос :

                     Q=Q1+Q2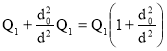  ;  Q=  ;  Q=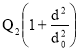

    Отсюда :

                      Q1=     ;    Q2=

    С учётом выражений для Q1 и Q2 формула (8) примет вид :

              Hн=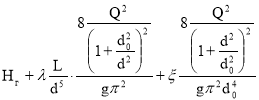                                      (9)

    Подставляя в (9) заданные числовые значения, получим :

              Hн=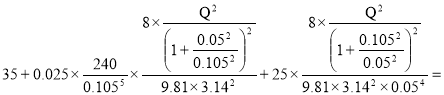

                                                    (10)

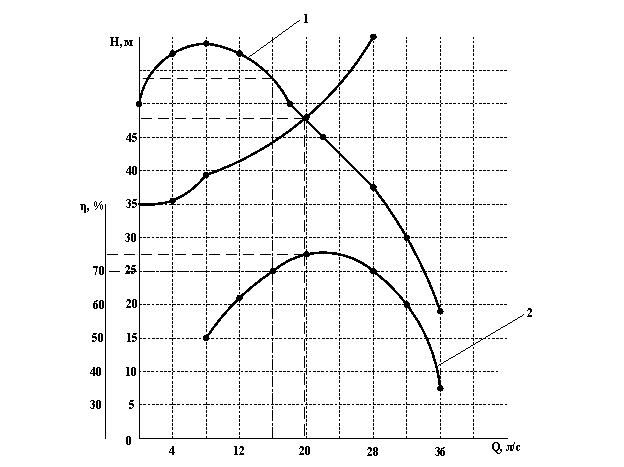
    На рисунке построены характеристики насоса H=f(Q) (линия 1) и η=f(Q) (линия 2). Построим характеристику насосной установки по выражению (10). Для этого составим таблицу :

Q, л/с	4	12	20	28	36
H, м	35.5	39.4	47.2	59	74.5

     Характеристика (линия 3) насосной установки построена на рисунке. На пересечении линий 1 и 3 находим рабочую точку насоса. По графику определяем подачу насоса (Q=20 л/c) и напор (H=47.5 м), а также КПД насоса – η=75%.

    Определяем потребляемую мощность насоса :

                        N=                                                                                (11)

    где Q – подача насоса ; H – его напор ; ρ=998 кг/м3 – плотность воды при t=20°C (табл. 1 [2])

    Вычисления по формуле (11) дают :

                         N1= Вт=12.4 кВт.

    Подача в верхний бак :

                         Q1=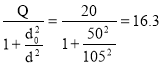 л/с

    Определим потребляемую насосом мощность, если такую же подачу Q1=16.3 л/с осуществлять в верхний бак с закрытой обводной линией. Т.е. подача насоса Q=Q1=16.3 л/с. По графику при Q=16.3 л/с находим H=53 м ; η=70%.

    Тогда вычисления по формуле (11) находим :

                        N2= Вт=12.1 кВт

    Ответ : Q1=16.3 л/с ; Q=20 л/с ; H=47.5 м ; N1=12.4 кВт ; N2=12.1 кВт.

 

 

 

 

                                                                          № 71.

    Определить полезную мощность насоса объёмного гидропривода, если внешняя нагрузка на поршень силового гидроцилиндра F, скорость рабочего хода v, диаметр поршня D1, диаметр штока D2. Механический коэффициент полезного действия гидроцилиндра ηмех=0.96, объёмный коэффициент ηоб=0.97. Общая длина трубопроводов системы l ; диаметр трубопроводов d ; суммарный коэффициент местных сопротивлений ζ=20. Рабочая жидкость в системе – спиртоглицериновая смесь (γ=12100 Н/м3 ; ν=9 см2/с).

    Указание. Напор насоса затрачивается на перемещение поршня, нагруженного силой F, а так же на преодоление гидравлических потерь в трубопроводах системы.

    Дано : F=80 кН ; v=11 см/с ; D1=138 мм ; D2=46 мм ; l=10 м ; d=25 мм.

    Найти : N

                                                                 Решение.

    Полезную мощность насоса вычислим по формуле :

                              N=QHγ                                                    (1)

    где Q – подача насоса ; H – напор, создаваемый насосом ; γ – удельный вес рабочей жидкости.

    Подача насоса равна расходу через цилиндр :

                               Q=v(S1-S2)=                      (2)

    Вычисления по формуле (2) дают :

                               Q= м3/с=1.5 л/с

    где v – скорость поршня ; S1, S2 – площадь сечения поршня и штока соответственно ; D1 и D2 – диаметр поршня и штока соответственно.

    Напор насоса, расходуемый на перемещение поршня, нагруженного силой F и преодоление гидравлических потерь, равен :

                                H=                                   (3)

    где p1 – давление в левой части цилиндра ; v – скорость поршня ; Δh – потери напора в трубопроводах системы.

    Давление перед поршнем найдём из условия равенства сил, действующих на поршень слева и справа :

                    ηмехη0p1(S1-S2)=F+p2(S1-S2)

    где p2 – давление в правой части цилиндра (так как истечение из правой части цилиндра происходит в открытый резервуар, то p2=pатм)

    Отсюда находим давление в левой части цилиндра :

                   p1=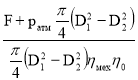                                    (4)

    Вычисления по формуле (4) дают :

                  p1=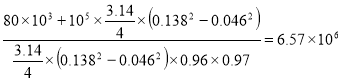 Па=6.57 МПа

    Потери напора в трубопроводах системы равны потерям напора по длине hℓ и потери напора в местных сопротивлениях hм :

                 Δh=hℓ+hм                                                            (5)

    Потери напора по длине, по формуле Вейсбаха-Дарси :

                                   hℓ=                                            (6)

    где v1 – скорость жидкости в трубопроводе ; λ – коэффициент гидравлического трения.

    Скорость жидкости в трубопроводе найдём из условия равенства расходов в трубопроводе и цилиндре :

                            

    Отсюда :

                            v1= м/с

    Число Рейнольдса по формуле :

                             Re=

    При Re<2300, режим движения – ламинарный. Поэтому коэффициент гидравлического трения определяем по формуле :

                             λ=                                                      (7)

    С учётом (7) формула (6) примет вид :

                            hℓ=                                          (8)

    Потери напора в местных сопротивлениях :

                            hм=                                                   (9)

    где ζ – суммарный коэффициент местных сопротивлений.

    Подставляя (8) и (9) в формулу (5), получим :

                            Δh=                  (10)

    Вычисления по формуле (10) дают :

                            Δh= м

    По формуле (3) вычислим напор насоса :

                          H= м

    Тогда, полезная мощность насоса по формуле (1) :

                          N=1.5×10-3×619.3×12100=11240 Вт=11.24 кВт

    Ответ : N=11.24 кВт.