Примеры решения задач по гидравлике
Задача 1.
Центробежный насос откачивает воду из сборного колодца в резервуар с постоянным уровнем H по трубопроводам размерами l1, d1 и l2, d2. Эквивалентная шероховатость поверхности труб Δ, плотность воды ρ=1000 кг/м3, кинематический коэффициент вязкости ν=0.01 см2/с, расстояние a=1 м.
Характеристики насоса представлены следующими параметрами :
|
Q, л/с |
0 |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
|
Hн, м |
45 |
47.5 |
48.5 |
48 |
47 |
45 |
40 |
35 |
30 |
22.5 |
15 |
|
Hдопвак, м |
- |
- |
8.2 |
8 |
7.6 |
7 |
6.6 |
6 |
5.5 |
4.75 |
4 |
При расчетах принять суммарные коэффициенты местных сопротивлений на всасывающей линии ξ1=10, на напорной линии ξ2=6.
Требуется определить :
1. На какой глубине h установится уровень воды в колодце, если приток в него Q?
2. Вакуумметрическую высоту всасывания при входе в насос Hвак, выраженную в метрах водяного столба (м в. ст.).
3. Максимальную допустимую геометрическую высоту всасывания при заданном расходе.
Дано : H=20 м ; l1=7 м ; l2=30 м ; d1=125 мм ; d2=100 мм ; Δ=1.5 мм ; Q=17 л/с ; ρ=1000 кг/м3 ; ν=0.01 см2/с ; a=1 м ; ξ1=10 ; ξ2=6.
Найти : h, Hвак, Hдопг.вс
Решение.
Пользуясь заданными в таблице параметрами, построим характеристики насоса : Hн=f(Q) и Hдопвак=f(Q).
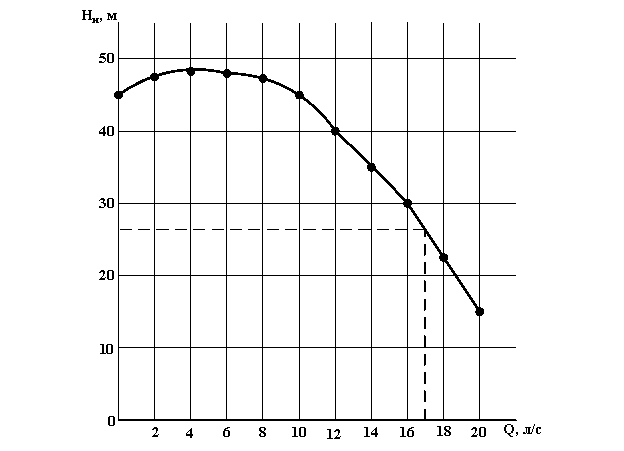
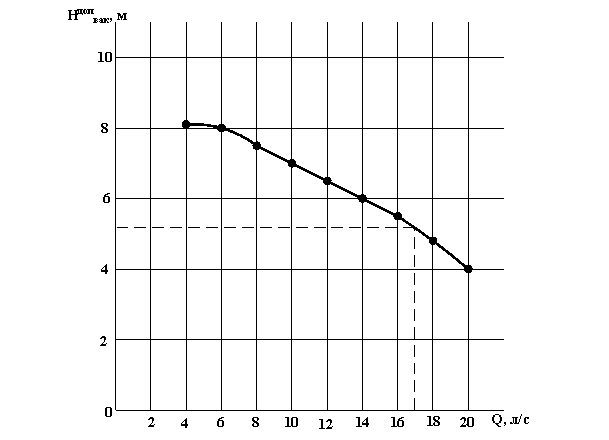
По построенным кривым, определяем, при заданном значении Q=6 л/с величины Hн=27 м, Hдопвак=5 м.
1. Напор, развиваемый насосом, расходуется на подъём воды на геометрическую высоту Hг=H+h и преодоление потерь напора во всасывающей и нагнетательной линиях :
Hн=Hг+h1+h2=H+h+h1+h2
Отсюда глубина, на котором установится уровень воды в колодце :
h=Hн-h1-h2 (1)
где Hн – напор, развиваемый насосом при заданном расходе Q (определяется по графику) ; h1 и h2 – потери напора во всасывающей и нагнетательной линиях.
Потери напора состоят из потерь напора по длине и в местных сопротивлениях :
h1=hℓ1+hм1 ; h2=hℓ2+hм2
Потери напора по длине определим по формуле Дарси :
hℓ1=
; hℓ2=
где λ – гидравлический коэффициент трения. Определяем по формуле Альштуля :
λ1=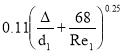
; λ2=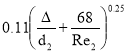
где Re – число Рейнольдса.
Скорость движения воды во всасывающей линии :
v1=
м/с.
Скорость движения жидкости в нагнетающей линии :
v2=
м/с.
Число Рейнольдса для всасывающей линии :
Re1=
Число Рейнольдса для нагнетающей линии :
Re2=
Гидравлический коэффициент трения для всасывающей линии :
λ1=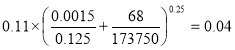
Гидравлический коэффициент трения для нагнетающей линии :
λ2=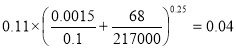
Потери напора по длине трубопровода для всасывающей линии :
hℓ1=
м.
Потери напора по длине трубопровода для нагнетающей линии :
hℓ2=
м.
Потери в местных сопротивлениях по формуле Вейсбаха :
для всасывающей линии :
hм1=
м ;
для нагнетающей линии :
hм2=
м.
Общие потери во всасывающей линии :
h1=0.22+0.98=1.2 м.
Общие потери в нагнетающей линии :
h2=2.88+1.44=4.32 м.
Тогда, искомая глубина, на которой установится уровень воды в колодце :
h=27-1.2-4.32=21.48 м.
2. Вакуумметрическую высоту всасывания при входе в насос определяем из уравнения Бернулли, составленного для сечений 1 – 1 и 2 – 2, приняв за горизонтальную плоскость сравнения сечение 1 – 1 :
Hвс=
(2)
Вычисления по формуле (2) дают :
Hвс=
Па.
или в метрах водного столба :
Hвс=23836 мм. в. ст.=23.8 м. в. ст.
3. Максимальную допустимую геометрическую высоту всасывания при заданном расходе определим по формуле :
(3)
где 
- допустимая вакуумметрическая высота всасывания (определяется по графику 
=5 м) ; h1 – потеря напора ; 
- скоростной напор во всасывающей линии ; α1 – коэффициент кинетической энергии потока (примем α1=1).
Вычисления по формуле (3) дают :
м.
Ответ : h=21.48 м ; Hвс=23.8 м. в. ст. ; =3.7 м.
Задача 2.
Жидкость плотностью ρ=900 кг/м3 поступает в левую полость цилиндра через дроссель с коэффициентом расхода μ=0.62 и диаметром d под избыточным давлением pн ; давление на сливе pс. Поршень гидроцилиндра диаметром D под действием разности давлений в левой и правой полостях цилиндра движется слева направо с некоторой скоростью v.
Требуется определить значение силы F, преодолеваемой штоком гидроцилиндра диаметром dш при движении его против нагрузки со скоростью v.
Дано : D=110 мм ; dш=55 мм ; d=2 мм ; pн=28 МПа ; pc=0.8 МПа ; v=5 см/с ; ρ=900 кг/м3 ; μ=0.62.
Найти : F.
Решение.
Силу, действующую на поршень определим, составив уравнение равновесия сил, действующих на поршень слева и справа :
F+pcS/=pрабS
или F+
;
F+
(1)
где pраб – давление в левой полости цилиндра ; S – площадь поршня в левой полости ; pc – давление в правой полости ; S/ - площадь поршня в правой полости.
Используя формулу расхода при истечении из отверстия определим давление p2, под действием которого происходит истечение через дроссель. Это давление равно разности давлений на входе в дроссель и в левой полости цилиндра p2=pн-pраб :
Q=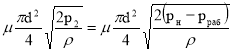
(2)
Расход через дроссель равен расходу через цилиндр и определяется по формуле :
Q=vS=
(3)
где v – скорость движения поршня.
Приравнивая правые части уравнений (2) и (3), получим :
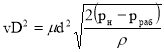
Отсюда находим давление в левой полости цилиндра :
pраб=
(4)
С учётом (4) формула (1) примет вид :
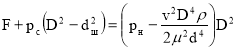
Отсюда значение силы :
F=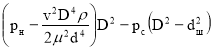
(5)
Вычисления по формуле (5) дают :
F=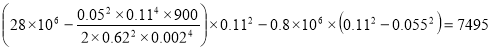
Н=7.5 кН
Ответ : F=7.5 кН.
Задача 3.
Определить давление, создаваемое насосом, если длины трубопроводов до и после гидроцилиндра, равны l ; их диаметры d ; диаметр поршня D ; диаметр штока dш ; сила на шток F ; подача насоса Q ; вязкость рабочей жидкости ν=0.5 см2/с ; плотность ρ=900 кг/м3.
Потери напора в местных сопротивлениях не учитывать.
Дано : l=13 м ; d=12 мм ; D=70 мм ; dш=40 мм ; F=2 кН ; Q=1.7 л/с ; ν=0.5 см2/с ; ρ=900 кг/м3.
Найти : pн.
Решение.
Давление, создаваемое насосом pн, затрачивается на преодоление потери давления Δp1 в подводящей линии и создание давления pп перед поршнем в цилиндре :
pн=Δp1+pп (1)
Необходимую величину давления перед поршнем pп найдём из условия равенства сил, действующих на поршень слева и справа :
pпSп=pш(Sп-Sш)+F
где pш – давление в цилиндре со стороны штока, равное потере давления в отводящей линии (pш=Δp2) ; Sп и Sш – соответственно площади поршня и штока.
Отсюда давление перед поршнем :
pп=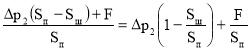
(2)
С учётом (2) формула (1) примет вид :
pн=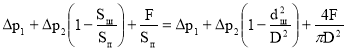
(3)
Скорость движения жидкости в подводящей линии :
v1=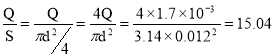
м/с.
где S – площадь сечения подводящей линии.
Скорость перемещения поршня :
vп=
м/с.
Расход жидкости, вытесняемой из штоковой области :
Qш=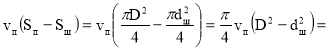
=
м3/с.
Скорость движения жидкости в отводящей линии :
v2=
м/с.
где S – площадь сечения отводящей линии.
Числа Рейнольдса соответствующие скоростям движения жидкости v1 и v2 :
Re1=
; Re2=
Так как, полученные числа Re1 и Re2 больше критического Reкр=2320, то движение жидкости в обоих случаях будет турбулентным. Поэтому гидравлический коэффициент трения λ определяем по формуле :
λ1=0.3164/Re10.25=0.3164/36100.25=0.041 ; λ2=0.3164/Re20.25=0.3164/24190.25=0.045
Потери давления в подводящей линии :
Δp1=
Па.
Δp2=
Па.
Тогда вычисления по формуле (3), окончательно, дают :
pн=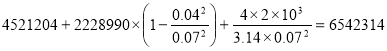
Па=6.5 МПа.
Ответ : pн=6.5 МПа.