Примеры решенных задач по физике - контрольная 8(молекулярная физика, равновесное излучение, ядерные реакции)

 

Задача 407.

Найти плотность газовой смеси, состоящей по массе из одной части водорода и восьми частей  кислорода при давлении и температуре

Дано :  

Найти g.

Решение. Пусть и - масса водорода и кислорода,  и - их парциальные давления, объём смеси газов. Согласно уравнению Менделеева – Клапейрона для водорода имеем

                                                                                                         ( 1 )

а для кислорода

                                                                                                         ( 2 )

где - молярная масса водорода, - молярная масса кислорода, - универсальная газовая постоянная. Сложим левые и правые части уравнений (1) и (2), учитывая, что - давление смеси газов:

                             

откуда объём

                        

Масса смеси поэтому её плотность

                                                                                    ( 3 )

Пусть масса одной части составляет Тогда масса частей водорода

а масса частей кислорода Подставляем значения

и в формулу (3):

                         

                         

Проверка размерности:

                         

Подставляем данные:

                         

Ответ:

 

  

Задача 417.

Найти среднее число столкновений в 1 секунду молекул углекислого газа при температуре если длина свободного пробега при этих условиях равна

Дано:  

Найти 

Решение. Среднее число столкновения в единицу времени рассчитывается по формуле

                                                                                                                    ( 4 )

где - средняя арифметическая скорость молекул, - средняя длина свободного пробега. В свою очередь скорость находится по формуле

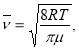                                                                                                               ( 5 )

где - молярная масса углекислого газа

Подставляем (5) в (4)

                          

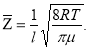
Проверка размерности:

                          

Подставляем данные:

                          

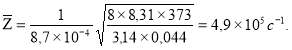
Ответ:

 

 

 

Задача 427.

В баллоне объёмом литров находится гелий под давлением и при температуре после того, как из баллона было взято гелия, температура в баллоне понизилась до Определить давление гелия, оставшегося в баллоне, и изменение внутренней энергии газа.

Дано:

Найти 

Решение. Пусть - начальная масса гелия. Запишем уравнение Менделеева – Клапейрона

                                                                                                    ( 6 )

где - молярная масса гелия. После изъятия из баллона гелия массой его масса становится равной и уравнение Менделеева – Клапейрона принимает вид

                                                              ( 7 )

Из (6) находим массу

                              

и подставляем её в (7)

                              

                              

откуда давление 

                                                                                                 ( 8 )

Начальная внутренняя энергия гелия

                              

а его конечная внутренняя энергия

                             

где - число степеней свободы молекулы. Изменение внутренней энергии.

                                                                    ( 9 )

Подставляем начальную массу в формулу (9)

                             

                                                                                 ( 10 )

Проверка размерности:

                              

                              

Подставляем данные в формулы (8) и (10), учитывая, что гелий – одноатомный газ, поэтому имеются только три поступательные степени свободы

                              

Отрицательный знак указывает на то, что внутренняя энергия гелия уменьшается.

Ответ:   

 

 

 

Задача 437.

Азот массой адиабатически расширили в

а затем изобарно сжали до первоначального объёма. Определить изменение энтропии DS газа в ходе указанных процессов.

Дано:    

Найти 

Решение. Процессы, в которых участвует газ, изображены на рис.1 на

- диаграмме.

 

 

 

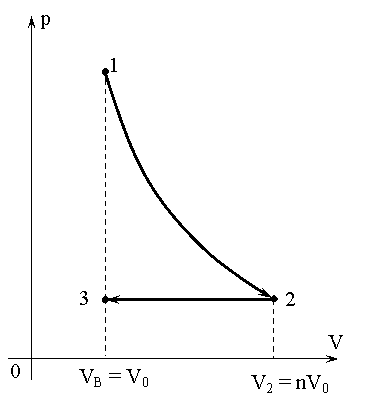
Процесс 1-2 представляет собой адиабатическое расширение, а процесс 2-3 – изобарное сжатие. Изменение энтропии в этих процессах

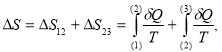                                                                                ( 11 )

где - подводимое к газу количество теплоты. При адиабатическом процессе газ теплоизолирован и Поэтому в данном процессе энтропия не изменяется:

При изобарном процессе при изменении температуры на малое значение

 

                                                                                                        ( 12 )

где - молярная теплоёмкость при постоянном давлении. Подставляем (12) в (11), получаем

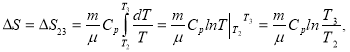                                                         ( 13 )

где температура газа в состояниях 2 и 3. При изобарном процессе

                                

поэтому

                                                                                                        ( 14 )

( см.рис.1). Молярная теплоёмкость при постоянном давлении

                                                                                                                  ( 15 )

При этом число степеней свободы для двухатомной молекулы азота Подставляя (14) и (15) в ( 13), окончательно получаем

                                

Проверка размерности:

                                

Подставляем данные:

                                

Видно, что энтропия при переходе газа из состояния 1 в состояние 3 уменьшается.

Ответ:

 

 

 

 

Задача 447.

За 5 мин. излучается энергия Площадь окошка  Принимая, что окошко излучает как абсолютно чёрное тело, определить температуру печи.

Дано:    

Найти

Решение. Излучаемая энергия равна

                                                                                                             ( 16 )

где энергетическая светимость, - площадь излучателя, промежуток времени. Согласно закону Стефана – Больцмана энергетическая светимость абсолютно черного тела

                                                                                                             ( 17 )

 

где - постоянная Стефана- Больцмана, - температура. Подставляем (17)в (16)

                                  

откуда находим температуру 

                                     

Проверка размерности:

                                    

Подставляем данные:

                                    

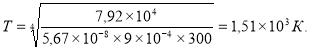
Ответ:  

 

 

 

  

Задача 457.

В одном акте деления ядра урана   освобождается энергия Определить: 1) энергию, выделяющуюся при распаде всех ядер этого изотопа урана массой 2) массу каменного угля с удельной теплотой сгорания

эквивалентную в тепловом отношении  урана

Дано:

Найти    

Решение. Если в одном анте деления выделяется энергия то при распаде ядер выделяется энергия

                                     

Рассчитаем количество ядер в уране массой Количество урана где - молярная масса изотопа Поэтому

                                      

где  постоянная Авогадро. Таким образом, выделяемая энергия

                                      

Эквивалентная в тепловом отношении масса каменного угля

                                       

Проверка размерности:

                                       

                                      

Подставляем данные, предварительно переведя энергию из в

 

 

                                

                                

                               

Ответ: 1)    2) 2,8 тысячи тонн.