Примеры решенных задач по физике - контрольная 6(гармонические колебания, электростатика)
1. Чем определяется вид траектории частицы, участвующей одновременно в двух взаимно перпендикулярных колебаниях?
Пусть уравнения колебаний имеют вид:
X=Asin(wt);
Y=Bsin(wt+j);
Определим уравнение траектории. Для этого исключим время из уравнений движения:
X/A=sin(wt); => cos(wt)=(1-(X/A)2)1/2
Y=B(sin(wt)*cos(j)+cos(wt)*sin(j));
Тогда:
Y=B(X/A* cos(j)+(1-(X/A)2)1/2 * sin(j)); =>
Y/B- X/A* cos(j)=(1-(X/A)2)1/2 * sin(j); =>
(Y/B)2+ (X/A)2* cos2(j)-2*X*Y/(A*B)* cos(j)= sin2(j) -(X/A)2* sin2(j) =>
(Y/B)2+(X/A)2* (sin2(j)+cos2(j)) - 2*X*Y/(A*B)* cos(j)= sin2(j) =>
Уравнение траектории:
(Y/B)2+(X/A)2 - 2*X*Y/(A*B)* cos(j)=sin2(j) =>
Вид траектории частицы зависит от амплитуд колебаний A , B и разности фаз между ними j. В общем случае это уравнение эллипса.
При A=B и j=p/2 получим уравнение окружности;
(Y/B)2+(X/A)2=1
При j=0 получим уравнение прямой;
(Y/B)2+(X/A)2 - 2*X*Y/(A*B)=0 =>(Y/B)=(X/A)
В остальных случаях получим уравнение эллипса.
2. Может ли энтропия убывать в ходе необратимого процесса?
Энтропия рабочего тела в ходе необратимого процесса, совершаемого над ним , убывать может - это не противоречит законам термодинамики. Но энтропия замкнутой системы, куда кроме рабочего тела включено все, совершающее работу над ним и совершающее теплообмен с ним, убывать не может – это противоречит второму началу термодинамики, согласно которому все процессы в замкнутой системе либо ведут к увеличению энтропии, либо оставляют ее неизменной.
3.Могут ли в ориентационно поляризованном диэлектрике молекулы, дипольные моменты которых образуют с направлением поля углы, близкие с p/2?
Молекулы диэлектрика будут участвовать в тепловом движении. Это значит, что их дипольные моменты не будут направлены в одном направлении постоянно, направление моментов будет хаотически меняться. В присутствии поля будет существовать преимущественное направление(по полю), в котором большинство молекул будет ориентировано в данный момент. Следовательно, в слабых полях такое может произойти, что в данный момент дипольные моменты некоторых молекул будут образовывать с направлением поля углы, близкие с p/2. Чем сильнее поле и меньше температура диэлектрика, тем меньше вероятность такого события.
4. Как, зная плотность тока в каждой точке некоторой поверхности, найти силу тока, текущего через эту поверхность?
Выделим малый элемент поверхности площадью dS с нормалью n. Обозначим dS=dS*n. Сила тока, текущего через эту поверхность, по определения плотности тока, равна
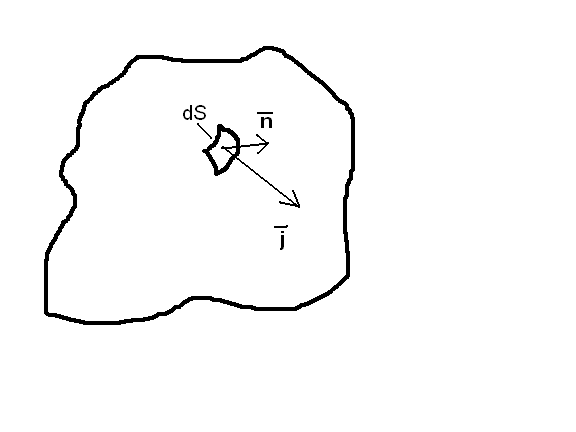
dI=j*n*dS=j*dS =>
Тогда сила тока текущего через всю поверхность, соответственно равна
I=ò dI =ò j*dS
5. При соблюдении каких условий напряженность магнитного поля не зависит от проницаемости среды?
Запишем теорему о циркуляции вектора Н в дифференциальном виде:
rotH=j;
где j- вектор плотности тока проводимости. Следовательно, напряженность магнитного поля создается токами проводимости и зависит только от них, и нет необходимости отдельно учитывать молекулярные токи и намагниченность. Помощь на экзамене онлайн. Получим, что напряженность магнитного поля не зависит от проницаемости среды в любом случае, так как она определяется только токами проводимости, а от магнитной проницаемости зависят вектор намагниченности среды J и вектор индукции поля B.
6.По тонкому стержню длиной l=0.2 м равномерно распределен заряд q=2.4*10-7 Кл. Стержень приведен во вращение с постоянной угловой скоростью w=10 с-1 относительно оси, перпендикулярной к стержню и проходящей через его середину. Определить : 1) магнитный момент, обусловленный вращением заряженного стержня; 2) отношение магнитного момента к моменту импульса (pm/L), если стержень имеет массу m=1,2*10-2 кг.
v(x)
![]()
![]() Дано: Решение. dx
Дано: Решение. dx
![]()
![]()
![]()
![]()
![]()
![]() l=0.2 м x
l=0.2 м x
q=2.4*10-7 Кл. w
![]()
![]()
![]() w=10 с-1
w=10 с-1
m=1,2*10-2 кг O
![]() l
l
![]() (pm/L), pm-?
(pm/L), pm-?
Выделим малый элемент стержня длиной dx на расстоянии x от оси вращения. Он несет заряд
dq=(q/l)*dx,
и обращается по окружности радиуса x за время T=2*p/w =>
эквивалентный круговой ток
dI=dq/T=q*w/(2*p*l)*dx
создает магнитный момент
dpm=dI*S= q*w/(2*p*l)*dx*p*x2=q*w*x2dx/(2l)
Весь стержень, следовательно, создает магнитный момент
pm= òdpm= q*w* /(2l)* ò x2dx= q*w* /(2l)*l3/3=q*w*l2/6
pm=2.4*10-7 Кл*10 с-1*(0.2 м)2/6=1.6*10-8 А*м2
Так как момент инерции стержня относительно оси вращения равен
J=ml2/12,
То момент импульса стержня
L=J*w= ml2w/12,
И искомое отношение
(pm/L)= q*w*l2/6*12/( ml2w)=2*q/m
(pm/L)=2*2.4*10-7 Кл/1,2*10-2 кг=4.0*10-5 Кл/кг
Ответ: pm=1.6*10-8 А*м2; (pm/L)= 4.0*10-5 Кл/кг.
