Примеры решенных задач по физике - контрольная 5(молекулярная физика, тепловое излучение, ядерная физика)

 

Задача №405

 Какой объем занимает смесь азота массой и гелия массой при нормальных условиях?

 

 Дано:

 

 

 Найти: V

 

 Решение:

 Запишем уравнение Менделеева-Клайперона для азота и для гелия

,  .  (1)

где и - парциональные давления азота и гелия, и - их массы, - молярная масса азота, - молярная масса гелия, - объем, - температура, - универсальная газовая постоянная.

 Сложим левые и правые части уравнений (1), учитывая, что давление смеси газов :

,

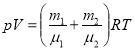откуда объем

.

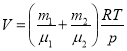 Проверка размерности:

.

 Подставим данные с учетом того, что при нормальных условиях давление и температура :

.

 

 Ответ:

 

 

 

 Задача №415

 В баллоне вместимостью содержится углекислый газ при температуре и давлении . Сколько столкновений происходит между молекулами за 1 секунду? Молярная масса углекислого газа . Эффективный диаметр молекул углекислого газа .

 Дано:

 

 

 

 

 

 

 Найти:

Решение:

 Среднее число столкновений одной молекулы за единицу времени

,      (2)

где 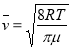- средняя арифметическая скорость молекул, - средняя длина свободного пробега, - концентрация молекул. Подставляем в (2) и :

.

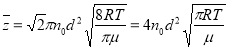 Концентрация молекул , где - число всех молекул. Поэтому

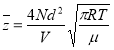    (3)

 Так как каждая молекула в единицу времени испытывает в среднем столкновений, а всего молекул , то за время количество всех столкновений равно

.     (4)

 Здесь учтено, что в каждом столкновении участвуют две молекулы, и множитель устраняет двойное суммирование при подсчете числа всех столкновений. Подставляем (3) в (4):

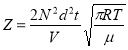.    (5)

 Рассчитываем число молекул

,

где - количество газа, - постоянная Авогадро. Величину находим из уравнения Менделеева-Клайперона:

,  .

 Тогда

.     (6)

 Подставляя (6) в (5), окончательно получаем

,

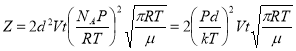где - постоянная Больцмана.

 Проверяем размерности:

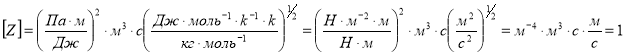 Подставляем данные

 

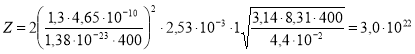
 Ответ: .

 

 Задача №425

 Азот массой нагревают при постоянном давлении от температуры до температуры . Какле количество теплоты поглощается при этом? Каков прирост внутренней энергии газа? Какая работа совершается газом?

Дано:

 

 

 

 Найти:

Решение:

 Согласно первому закону термодинамики теплота Q, подводимая к газу, расходуется на увеличение его внутренней энергии и на совершение газом работы :

     (7)

 Работа газа при постоянном давлении

,

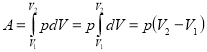где - начальный объем, - конечный объем.

 Воспользуемся уравнением Менделеева-Клапейрона:

,  ,

где - молярная масса азота. Тогда

.  (8)

 Внутренняя энергия газа , где - число степеней свободы молекулы (для двухатомных молекул азота ). Тогда прирост внутренней энергии при изменении температуры от до

. (9)

 Подставляем (8) и (9) в (7), находим количество теплоты

.

 Проверка разности:

.

 Подставим данные:

.

.

.

 Ответ: ; ;

 Задача №435

 Во сколько раз необходимо увеличить объем идеального газа при изотермическом расширении, если его энтропия увеличилась на ?

Дано:

 

 

 Найти:

Решение:

 Изменение энтропии идеального газа

,     (10)

где - бесконечно малое количество теплоты, подводимое к газу, - температура. В изотермическом процессе температура постоянна, внутренняя энергия газа не изменяется, поэтому подводимая к газу теплота полностью расходуется на совершение газом работы:

 С учетом этого формула (10) принимает вид

,

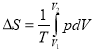где - начальный объем, - конечный объем. Из уравнения Менделеева-Клайперона находим давление :

,  

 Тогда

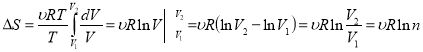,  (11)

где - количество раз, в которое увеличивается объем. Из (11) находим :

,  

 Подставляем данные:

 Ответ: в раза.

 

 

 

 

 Задача №445

 Какого цвета будет звезда, если температура ее поверхности ? Какую энергию излучает звезда за 1 секунду с единицы поверхности?

Дано:

 

 Найти: ,

Решение:

 Длина волны, на которую приходится максимум энергии излучения, находится из закона смещения Вина

,

где - постоянная Вина.

 Энергия, излучаемая за единицу времени с единицы поверхности, представляет собой энергетическую светимость тела. Предполагая, что звезда излучает как абсолютно черное тело, находим энергетическую светимость по закону Стефана-Больцмана

,

где - постоянная Стефана-Больцмана.

 Подставляем данные:

,

.

 Длина волны соответствует излучению красного цвета.

 Ответ: красного;

 

 

 Задача №455

 Ядро урана испуская - частицу с энергией превращается в ядро тория . Определить массу атома , если масса атома равна

Дано:

 

 

 Найти:

Решение:

 Уравнение ядерной реакции

.

 Дефект массы

,   (12)

где , и - массы нейтральных атомов урана , тория и гелия . Величина действительно представляет дефект массы ядер, поскольку массы электронов, входящих в состав атомов, в правой части формулы (12) сокращаются. Согласно формуле Эйнштейна энергия - частицы

,     (13)

где - скорость света в вакууме. Подставляем (12) в (13) и находим массу :

,

 подставляем данные, учитывая, что квадрат скорости света

 Имеем

 Ответ: