Примеры решенных задач по физике - контрольная 4(молекулярная физика и термодинамика)

   № 504

Найти среднюю квадратичную, среднюю арифметическую и наиболее вероятную скорости молекул водорода. Вычисления выполнять для температуры 300 К.

Дано: Т = 300 К.

Найти:    , ,   Vв.             

Решение.

  Средняя арифметическая скорость молекул выражается формулой

   =                           (1)

где Т- температура газа ; R- молярная газовая постоянная [R=8,31 Дж/(моль К)] ; M- моляр-   ная масса газа (для водорода М=0,002 кг/моль).

  Средняя квадратическая скорость молекулы газа  выражается формулой:

                                                 =                                   (2)

    Наиболее вероятная скорость молекул газа:

Vв =       (3)

 

Находим:

 

=1781,6 м/с;

 

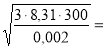=1933,8 м/с;

 

Vв=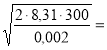1578,9 м/с.

    № 514.

    Определить молярную массу газа, если при температуре Т=300 К и давлении p=0,2 МПа он имеет плотность ρ=2,41 кг/м3.

    Дано : T= 300 K

                 P= 2×105 Па

                 ρ=2,41 кг/м3

    Найти:                                                    Решение.

    Для решения задачи воспользуемся уравнением Менделеева-Клапейрона, записанного в виде:

                P=                (1)  ,  где ρ – плотность газа; R – молярная газовая постоянная (R  =8.31 Дж/(моль∙К)) ; T – температура газа ; P – давление газа ; μ – молярная масса газа.

 

     Выражая из (1) молярную массу μ, получим :

           =                 (3)

    Подставляя, заданные числовые значения физических величин в формулу (3) и вычисляя, получим :

           ==0,03 кг/моль

    Ответ :  =0,03 кг/моль.  

 

 

   № 524

  Найти отношения  теплоёмкостей Cp/Cv для газовой смеси, состоящей из 10 г гелия и 25 г водорода?

  Дано: газ He

               газ Н2

               ν1= m1/M1 = 10/4 =2,5 моль

              ν2= m2/M2 = 25/2 = 12,5 моль

  Найти : Cp/Cv                                                    Решение.

  Молярную теплоёмкость смеси Cv при постоянном объёме найдём следующим. Теплоты, необходимую для нагревания смеси на ΔТ, выразим двумя способами :

  Q=Cv(ν1+ν2)ΔT               (1)

  Q=(Cv1ν1+Cv2ν2)ΔT       (2)

  где Cv1 – молярная теплоёмкость гелия ; Cv2 – молярная теплоёмкость кислорода.

  Приравняв правые части (1) и (2) и разделив обе части полученного равенства на ΔТ, получим :

  Cv(ν1+ν2)=Cv1ν1+Cv2ν2  , откуда

  Cv=(Cv1ν1+Cv2ν2)/(ν1+ν2)                          (3)

  Рассуждая так же, получим формулу для вычисления молярной теплоёмкости при постоянном давлении :

  Cp=(Cp1ν1+Cp2ν2)/(ν1+ν2)                          (4)

  Вычислим отношение формул (4) и (3), получим :

  Cp/Cv=(Cp1ν1+Cp2ν2)/(Cv1ν1+Cv2ν2)             (5)

  Молярные теплоёмкости газа при постоянном объёме и давлении выражаются соответственно :

  Cv=iR/2  ;  Cp=(i+2)R/2  , где i – число степеней свободы молекулы газа.

  Используя эти выражения запишем формулы для молярных теплоёмкостей гелия и кислорода.

  Сv1=i1R/2    (6)  ;  Cp1=(i1+2)R/2       (7)  ,где i1=3  (так как молекула гелия одноатомная).

  Сv2=i2R/2    (8)  ;  Cp2=(i2+2)R/2       (9)  , где i2=5  (так как молекула водорода двухатомная).

  Подставляя, полученные выражения (6), (7), (8) и (9) в формулу (5), получим :

  Cp/Cv=[(i1+2)ν1+(i2+2)ν2]/(i1ν1+i2ν2)   (10)

  Произведя вычисления, получим :

  Cp/Cv=[(3+2)∙2,5+(5+2)∙12,5]/(3∙2,5+5∙12,5)= 1,4286 Дж/(К моль)

  Ответ : Cp/Cv=1,4286 Дж/(К моль).

 

 

№534

    Найти среднюю длину свободного пробега молекулы азота в сосуде объемом 6 л. Масса газа 0,5 г.

    Дано : d=3×10-8 см=3×10-11 см

                 p=105 Па

                 T=273 K

    Найти :            

                                                                        Решение.           

    Средняя длина свободного пробега молекул газа выражается формулой :

                                        =1/πd2n                                                      (1)

    где d – диаметр молекулы ; n – концентрация молекул.

    Концентрация молекул связана с давлением и температурой газа выражением:

                              n=p/kT                                                                              (2)

    где к – постоянная Больцмана (к=1.38×10-23 Дж/К)

    Из уравнения Менделеева-Клайперона можем записать:

      (3)

, где V – объем газа, R – молярная газовая постоянная, m и M – масса и молярная масса газа соответственно.

Подставляя (3) в (2), а затем в выражение (1), получим:

                            =                                                                      (4)

    Вычисления по формуле (4) дают

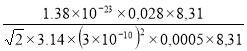                            == 1,9336×10-3 м

 

    Ответ: =1,9336×10-3 м.

 

 

 

 

 

 

 

 

 

 

 

 

 

№ 546

    Газ, для которого γ=Cp/Cv=4/3, находится под давлением P=2×105 Па и занимает объём V=3 дм3. В результате изобарического нагревания объём увеличился в 3 раза. Определить количество теплоты, переданное газу.

    Дано : γ=Cp/Cv=4/3

                 P=2×105 Па

                 V=3 дм3=3×10-3 м3

                 V2/V=3

    Найти : Q

                                                                     Решение.

    Количество теплоты, участвующее в изобарном процессе выражается формулой :

                            Q=             (1)  , где m – масса газа ; M – молярная масса газа ; Cp – молярная теплоёмкость при p=const ; ΔT – изменение температуры газа.

    Изменение температуры газа :

                            ΔT=T2-T1                      (2)

    Начальную Т1 и конечную Т2 температуры газа найдём из уравнения Менделеева-Клапейрона :

                            T1=        (3)  ;   T2=   (4) 

    где V и V2 – объёмы газа до нагревания и после, соответственно.

    С учётом выражений (3) и (4), формула (2) примет вид :

                          ΔT=                                (5)

    Подставляя полученное выражение для ΔТ согласно (5) в уравнение (1), получим :

                        Q=                 (6)

    С учётом уравнения : R=Cp-Cv выражение (6) примет вид :

                         Q=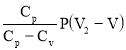

   Разделив числитель и знаменатель последнего выражения на Cv и, учитывая, что V2=3V, получим :

                           Q=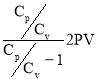                                       (7)

    Произведя вычисления по формуле (7), найдём количество теплоты, подведённое к газу :

                             Q=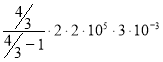=4800 Дж=4.8 кДж

    Ответ : Q=4.8 кДж.

 

 

 

 

 

 

 

№ 556

    Во сколько раз необходимо увеличить объём ν=5 моль идеального газа при изотермическом расширении, если его энтропия увеличилась на ΔS=57.6 Дж/К?

    Дано : ν=5 моль

                 T=const

                 ΔS=57.6 Дж/К

    Найти : V2/V1

                                                                      Решение.

    Как известно, изменение энтропии выражается общей формулой :

                     ΔS=S2-S1=                            (1)

    При вычислении по формуле (1) вынесем температуру Т за знак интеграла (при изотермическом процесс T=const). Вычислив интеграл, найдём :

                      ΔS=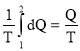                         (2)

    где Q – количество теплоты.

    Количество теплоты при изотермическом процессе выражается формулой :

                        Q=νRTln(V2/V1)                      (3)

     С учётом (2) уравнение (3) примет вид :

                       ΔS=  

    Отсюда изменение объёма газа :

               V2/V1=                                  (4)

    Вычисления по формуле (4) дают :

               V2/V1==4

    Ответ : объём газа необходимо увеличить в 4 раза.