Примеры решенных задач по физике - контрольная 3(молекулярная физика)
Ниже приведены условия и решения задач. Закачка решений в формате doc начнется автоматически через 10 секунд.
Вариант 2
- Имеется идеальный газ, молярная теплоемкость
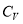 которого известна. Газ совершает процесс по закону
которого известна. Газ совершает процесс по закону 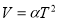 , где
, где 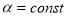 . Найти: а) молярную теплоемкость
. Найти: а) молярную теплоемкость 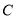 газа как функцию его температуры
газа как функцию его температуры 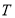 ; б) сообщенное газу тепло при его расширении от
; б) сообщенное газу тепло при его расширении от 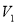 до
до 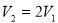 .
.
Решение:
а)
Молярная теплоемкость газа:
![]()
По первому началу термодинамики
![]()
Внутренняя энергия газа:
![]()
Тогда изменение внутренней энергии газа:
![]()
Кроме того,
![]()
Поскольку, по условию, ![]()
то,
![]()
Согласно уравнению Менделеева – Клапейрона ![]()
С учетом того, что по условию ![]() , имеем
, имеем ![]()
Тогда
![]()
Следовательно,
![]()
![]()
б)
выше получено соотношение ![]() =>
=> ![]()
Тогда ![]()
![]()
Поскольку ![]() , то
, то
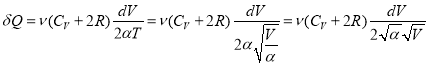
Тогда при расширении газа сообщенное ему количество теплоты:
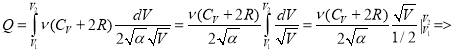
![]()
- Двухатомный идеальный газ занимает объем
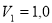 л и находится под давлением
л и находится под давлением 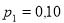 МПа. После адиабатного сжатия газ характеризуется объемом
МПа. После адиабатного сжатия газ характеризуется объемом 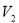 и давлением
и давлением 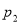 . В результате последующего изохорного процесса газ охлаждается до первоначальной температуры
. В результате последующего изохорного процесса газ охлаждается до первоначальной температуры 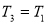 , а его давление
, а его давление 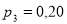 МПа. Определите: а) определите объем
МПа. Определите: а) определите объем 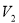 и давление
и давление 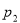 газа в состоянии 2; б) работу газа, изменение его внутренней энергии и количество теплоты, полученное газом в процессе
газа в состоянии 2; б) работу газа, изменение его внутренней энергии и количество теплоты, полученное газом в процессе 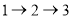 .
.
Решение:
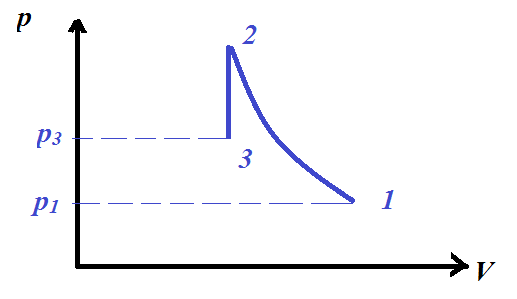
а) Уравнение адиабаты:
![]()
![]() (1)
(1)
Постоянная адиабаты ![]() , для двухатомного газа число степеней свободы i=5 (если молекулу считать жесткой, что справедливо при не высоких температурах), тогда
, для двухатомного газа число степеней свободы i=5 (если молекулу считать жесткой, что справедливо при не высоких температурах), тогда ![]() .
.
Согласно уравнению Менделеева-Клапейрона можем записать:
![]()
![]() (2)
(2)
![]()
Здесь мы учли, что ![]()
Из уравнений (2) получаем:
![]()
![]() (3)
(3)
Из (1) и (3) получаем:
![]()
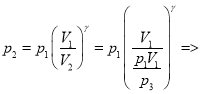
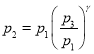 (4)
(4)
б)
Работа газа:
![]() - в общем случае.
- в общем случае.
В адиабатическом процессе
![]() (5)
(5)
При изохорном процессе изменение объема равно 0, поэтому работа также равна нулю: ![]() . Таким образом, из (5) и (2) имеем:
. Таким образом, из (5) и (2) имеем:
![]()
С учетом (3-4):
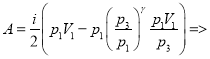
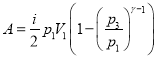 (6)
(6)
Внутренняя энергия газа:
![]()
Тогда изменение внутренней энергии газа в результате всего процесса:
![]()
По условию, ![]() , поэтому внутренняя энергия газа в процессе 1-2-3 не изменится:
, поэтому внутренняя энергия газа в процессе 1-2-3 не изменится:
![]() (7)
(7)
Количество теплоты, полученное в процессе 1-2, равно 0, поскольку процесс адиабатический: ![]() .
.
Количество теплоты, полученное в процессе 2-3
![]()
![]() (с учетом
(с учетом ![]() )=
)=![]() (с учетом (3-4))=
(с учетом (3-4))= 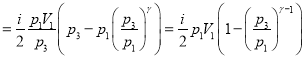
В итоге
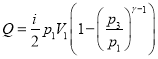 (8)
(8)
Видно, что правая часть (8) совпадает с (6), т.е. в рассматриваемом процессе А=Q.
Произведем расчет согласно формулам (3-4), (6-8):
![]() 0,5 л
0,5 л
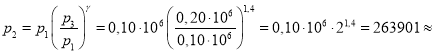 0,26 МПа
0,26 МПа
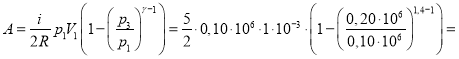
![]() Дж
Дж
![]()
![]() ‑79.9 Дж
‑79.9 Дж
- Азот массой
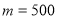 г, находящийся под давлением
г, находящийся под давлением 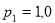 МПа при температуре
МПа при температуре 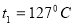 , изотермически расширяется, в результате чего давление газа уменьшилось в
, изотермически расширяется, в результате чего давление газа уменьшилось в 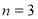 раза. После этого газ адиабатно сжимают до начального давления, а затем изобарно сжимают до начального объема. Постройте график цикла и определите работу, совершенную газом за цикл, и холодильный коэффициент.
раза. После этого газ адиабатно сжимают до начального давления, а затем изобарно сжимают до начального объема. Постройте график цикла и определите работу, совершенную газом за цикл, и холодильный коэффициент.
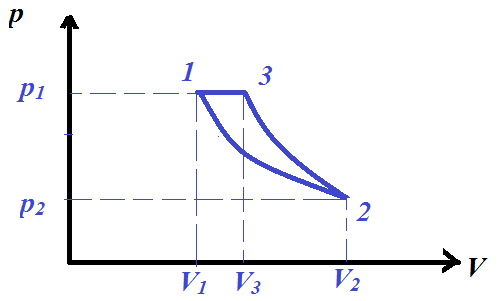
Работа газа:
![]() (1)
(1)
В изотермическом процессе:
![]() (2)
(2)
Здесь n=3, согласно условию.
Согласно уравнению Менделеева - Клапейрона можем записать:
![]()
![]() (3)
(3)
![]()
Здесь мы учли, что ![]()
Уравнение адиабаты:
![]()
![]() (4)
(4)
Учитывая ![]() , из (4) имеем:
, из (4) имеем:
![]() (5)
(5)
Из (5) получаем:
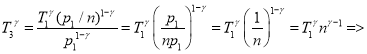
![]() (6)
(6)
Постоянная адиабаты ![]() , для двухатомного газа (в т.ч. азота) число степеней свободы i=5 (если молекулу считать жесткой, что справедливо при не высоких температурах), тогда
, для двухатомного газа (в т.ч. азота) число степеней свободы i=5 (если молекулу считать жесткой, что справедливо при не высоких температурах), тогда ![]() .
.
В адиабатическом процессе:
![]() =(с учетом (6), а также
=(с учетом (6), а также ![]() )
)![]()
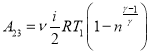 (7)
(7)
В изобарном процессе работа:
![]() =(с учетом (6))=
=(с учетом (6))=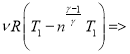
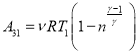 (8)
(8)
Тогда из (1), (2), (7), (8):
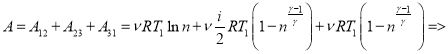
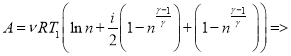
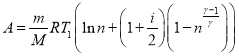 (9)
(9)
Холодильный коэффициент равен отношению количества теплоты, которая передается газу за цикл, к работе внешних сил, совершенной за цикл.
Работа внешних сил равна работе газа с обратным знаком: ‑A.
Найдем количество теплоты, переданное газу. В данном цикле теплота передается газу на этапе изотермического расширения (в адиабатическом процессе теплота не передается и не отнимается, на этапе изобарного сжатия теплота отбирается от газа).
По первому началу термодинамики
![]()
В изотермическом процессе ![]() =0, работа газа найдена выше
=0, работа газа найдена выше ![]()
Следовательно,
![]()
Тогда холодильный коэффициент
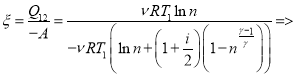
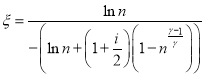 (10)
(10)
Произведем расчет по (9-10):
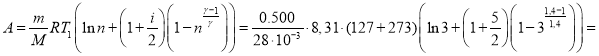 ‑11395 Дж
‑11395 Дж
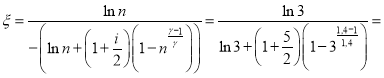 5,7
5,7
- Найти приращение энтропии алюминиевого бруска массы
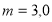 кг при нагревании его от
кг при нагревании его от 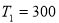 К до
К до 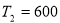 К, если в этом интервале температур удельная теплоемкость алюминия
К, если в этом интервале температур удельная теплоемкость алюминия 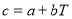 , где
, где 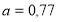 кДж/(кг∙К),
кДж/(кг∙К), 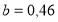 Дж/(кг∙К2).
Дж/(кг∙К2).
Приращение энтропии:
![]()
Тогда при изменении температуры от Т1 до Т2:
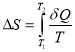
Для изменения температуры бруска на dT ему следует сообщить количество теплоты, равное
![]()
Тогда
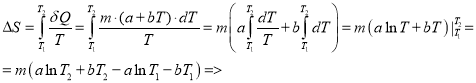
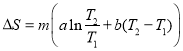
Произведем расчет:
![]() 415,6 Дж/К ≈ 4,2*10‑2 Дж/К
415,6 Дж/К ≈ 4,2*10‑2 Дж/К
- Термодинамический потенциал
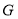 одного моля некоторого вещества дается выражением
одного моля некоторого вещества дается выражением 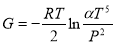 , где
, где 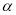 − некоторая константа. Найти: а) теплоемкость
− некоторая константа. Найти: а) теплоемкость 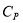 этого вещества; б) явный вид термодинамического потенциала внутренняя энергия
этого вещества; б) явный вид термодинамического потенциала внутренняя энергия 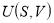 .
.
a) Учтем известные из термодинамики соотношения ![]()
Тогда
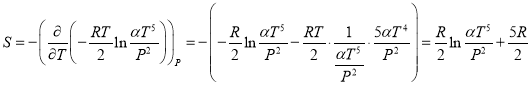
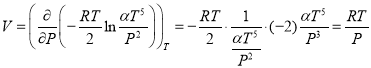
Теплоемкость:
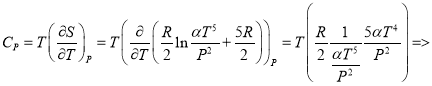
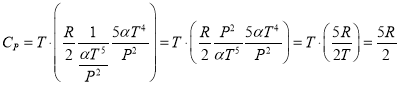
б) Связь потенциала Гиббса G и внутренней энергии:
![]()
![]() с учетом условия задачи:
с учетом условия задачи:
![]()
Из выражения для S имеем:
![]()
![]()
![]()
Получаем для внутренней энергии
![]()
![]()
Из выражения для V имеем:
![]() (отметим, что выражение совпадает с уравнением Менделеева-Клапейрона для 1 моля идеального газа).
(отметим, что выражение совпадает с уравнением Менделеева-Клапейрона для 1 моля идеального газа).
Тогда
![]() или
или ![]() - известные выражения для внутренней энергии идеального газа.
- известные выражения для внутренней энергии идеального газа.
- На какой высоте
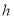 плотность воздуха составляет 60% от плотности воздуха на уровне моря? Считать, что температура воздуха не зависит от высоты и равна
плотность воздуха составляет 60% от плотности воздуха на уровне моря? Считать, что температура воздуха не зависит от высоты и равна 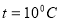 .
.
Барометрическая формула для плотности воздуха:
![]()
Отсюда для ![]() получаем
получаем
![]()
![]()
Учитывая, что молярная масса воздуха М=0,029 кг/моль, получаем
![]() = 4227 м ≈ 4,2*103 м
= 4227 м ≈ 4,2*103 м
- Коэффициент диффузии кислорода при
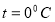 и
и 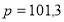 кПа равен
кПа равен 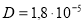 м2/с. Оценить среднюю длину свободного пробега
м2/с. Оценить среднюю длину свободного пробега 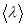 молекул кислорода при тех же условиях.
молекул кислорода при тех же условиях.
Коэффициент диффузии:
![]()
Здесь ![]() - среднеквадратичная скорость молекул,
- среднеквадратичная скорость молекул, ![]() - средняя длина свободного пробега молекул.
- средняя длина свободного пробега молекул.
Среднеквадратичная скорость
![]()
Здесь d – диаметр молекулы, n – концентрация молекул.
Тогда
![]()
Поскольку давление газа
![]()
То
![]()
Произведем расчет
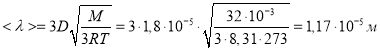
- Для определения постоянных Ван-дер-Ваальса некоторое количество газа, занимающего при
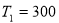 К и
К и 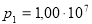 Па объем
Па объем 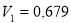 л, было изотермически сжато до объема
л, было изотермически сжато до объема 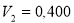 л, в результате чего давление возросло до значения
л, в результате чего давление возросло до значения 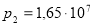 Па. Затем газ был охлажден при неизменном объеме до температуры
Па. Затем газ был охлажден при неизменном объеме до температуры 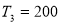 К, и давление при этом уменьшилось до значения
К, и давление при этом уменьшилось до значения 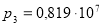 Па. Воспользовавшись этими данными, вычислить постоянные
Па. Воспользовавшись этими данными, вычислить постоянные 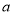 и
и 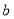 для данного газа.
для данного газа.
Уравнение газа Ван-дер-Ваальса:
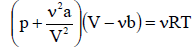
Получаем:
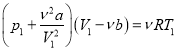 (1)
(1)
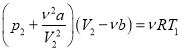 (2)
(2)
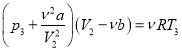 (3)
(3)
Решение этих уравнений в общем виде весьма громоздко. Для упрощения решения подставим численные значения. Получаем:
![]() (4)
(4)
![]() (5)
(5)
![]() (6)
(6)
Раскрывая скобки, получим:
![]() (7)
(7)
![]() (8)
(8)
![]() (9)
(9)
Вычитая из первого полученного уравнения (7) второе (8), получаем:
![]() (10)
(10)
Вычитая из уравнения (8) уравнение (9), получаем:
![]() (11)
(11)
Из (11) получаем:
![]() (12)
(12)
Подставляя (12) в (11), получаем:
![]() (13)
(13)
Выразим а из (13):
![]() (14)
(14)
Подставим формулы для ν (12) и для а (14) в (7):
+
![]() +
+
+ ![]() =
= ![]() (15)
(15)
Домножая на (1+10000b), получим:
![]()
![]()
Приводя подобные слагаемые, получаем:
![]()
Отсюда
![]()
Окончательно
![]() (16)
(16)
Подставляя (16) в (14), получаем:
![]()
![]() 0,149
0,149
В итоге имеем:
а≈0,149 м3·Па/моль2
b≈3,32•10‑5 м3/моль
1
Имя файла: Physics3.doc
Размер файла: 505.5 Kb
Если закачивание файла не начнется через 10 сек, кликните по этой ссылке
