Примеры решенных задач по физике - контрольная 10(механика - второй закон Ньютона, сила трения, закон сохранения импульса, теория относительности)

Задача № 107.

Тело падает без начальной скорости с высоты h=45 м. Определите среднюю скорость  на второй половине пути.

Дано: h=4м.

Найти .

Решение. Пусть t1 – время, за которое тело проходит первую половину пути, а t2 – время, за которое тело проходит весь путь. Тело движется равномерно с ускорением свободного падения

g = 9,81 м/с2. Поэтому

,         h=,

 

откуда

t1= ,          t2 =.

Тогда время , за которое тело проходит вторую половину пути

- t=.

 

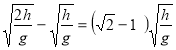Так как вторая половина пути составляет s=,то средняя скорость

.

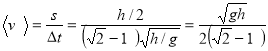Проверка разности:

.

 

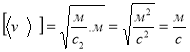Подставляем данные

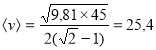м/с.

Ответ: 25,4 м/с.

 

Задача № 127.

Если к телу приложить силу F=120 H под углом   =60о к горизонту, то тело будет двигаться равномерно. С каким ускорением будет двигаться тело, если ту же силу приложить под углом =30о к горизонту? Масса тела m = 25 кг.

Дано: F=120 H, m=25 кг, =60о, =30о.

Найти : .

Решение. На тело действует внешняя сила , сила тяжести  m, сила реакции опоры и сила трения ( см. рис.1). По второму закону Ньютона

 

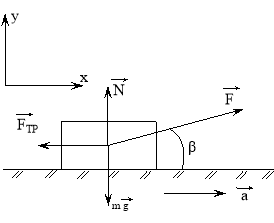
,                                                                                                     ( 1 )    

Где  - ускорение тела. Направим координатную ось x вдоль направления движения, а координатную ось у перпендикулярно опоре ( рис.1). Проецируем векторное уравнение (1) на оси х и у:

,            .                                                           ( 2 )

Из второго из  уравнений ( 2 ) . сила трения скольжения

, где - коэффициент трения. Поэтому первое из уравнений ( 2 ) принимает вид

.                                                                                           ( 3 )

Если сила F приложена под углом  , то ускорение тела   .

Заменим в (3) угол    на    и положим   :

,

откуда коэффициент трения

.

Далее подставляем (4) в (3):

,

откуда ускорение тела

.

Проверка разности:  .

Подставляем данные: .

 

Ответ: 1,0 м/с2.

 

Задача № 157

Шар массой   m1 =1,0 кг, двигаясь со скоростью v1=6,0 м/с, догоняет другой шар массой  

m2 =1,5 кг, двигающийся по тому же направлению со скоростью v2= 2,0 м/с. Происходит упругое центральное столкновение. Найдите скорость v1 и v2 первого и второго шаров после удара.

Дано: m1 =1,0 кг, m2 =1,5 кг,  v1=6,0 м/с,  v2= 2,0 м/с.

Найти: v1/ , v2/ .

Решение. На рис.2 а) показано движение шарика до столкновения, а на рис.2 б) – после столкновения.

 

 

 

 

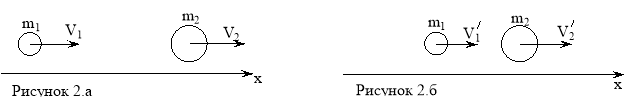
Согласно закону сохранения импульса

.проецирую это уравнение на ось х, параллельную векторам скоростей, имеем

.                                                                                                     ( 5 )

Так как столкновение шаров упругое, полная механическая энергия ( сумма кинетических энергий шаров) сохраняется:

,    .                          ( 6 )

Преобразуем уравнения ( 5 ) и ( 6 ):

,                                                                                                      ( 7 )

,   .                    ( 8 )

Разделим ( 8 ) в ( 7 ): , откуда

.                                                                                                                     ( 9 )

Подставим ( 9 ) в ( 7 ) и найдём скорость первого шарика после столкновения :

,

.                                                                                                ( 10 )

Теперь подставим ( 10 ) в ( 9 ) и найдём скорость второго шара:

,

.

Проверка разности :. Подставляем данные :

,

.

Положительные значения и v2/ указывают на то, что после столкновения шары не изменяют направления движения на противоположные.

Ответ: 1,2 м/с;  5,2 м/с.

 

 

 

 

 

Задача № 167

Каков возраст космонавта по часам Земли, если он в 30-летнем возрасте улетел на расстояние до 20 св. лет. Считать его возраст по часам космонавта 35 лет.

Дано: То=30 лет, Т/ =35 лет, l =20 св. лет.

Найти: Т.

Решение. Пусть при вылете космонавта часы на Земле и на корабле были синхронизированы и показали нулевое время. Считая, что космонавт движется равномерно и прямолинейно со скоростью v , находим показания земных часов при его удалении на расстояние l:

          t=.                                                                                                                             ( 11 )

Часы на корабле покажут время t/ , определяемое из преобразований Лоренца:

          t/ =,                                                                                                          ( 12 )

где x = l – координата корабля, с – скорость света в вакууме. Подставляем ( 11 ) в ( 12 ):

 

         t/ = ,       

откуда находим скорость v :  

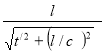v2 t/2 = l2 ( 1 – v2/с2 ) ,       v2 ( t/ 2 + ( ,   v = .                          ( 13 )

Подставляем ( 13 ) в ( 11 )  :

t = .                                                                                                              ( 14 )

Возраст космонавта отсчитывается от значения Tо , поэтому его возраст по земным часам

T = Tо + t   ,а по космическим – T/ = Tо + t/ . 

Формула ( 14 ) принимает вид

T – To =          T = To +       

 

 

 

Подставляем данные, учитывая то, что      20 лет:

T = 30 + лет.

 

Ответ: 50,6 лет.       

 

 

Задача  195.

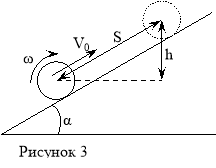
Какой путь S пройдет катящийся без скольжения диск, поднимаясь вверх по наклонной плоскости с углом наклона начальная скорость диска параллельно наклонной плоскости и равна vo = 7,0 м/с.

Дано: , vo = 7,0 м/с.

Найти:   S.

Решение:

 

 

 

 

 

. воспользуемся законом сохранения энергии. В начале диск имеет  только кинетическую энергию поступательного и вращательного движения:

,

Где m – масса диска, Z – его момент инерции, vo –  начальная скорость, - начальная угловая скорость. Так как скольжения нет, то , где R – радиус диска. Считая, что диск однородный. Принимаем . В результате имеем

.

В конце подъёма у диска имеется только потенциальная энергия

, где h – высота подъёма центра масс ( рис.3 ). Так как , то

,            .

с другой стороны, высота  h выражает через пройденный путь S как h = S  sin. Поэтому

.

Проверка разности: . Подставляем данные:

Ответ:  7,5 м.

 

Задача  205.   

Стальной шарик диаметром d = 1мм падает с постоянной скоростью v = 0,185 см/с в большом сосуде, наполненном маслом. Определите коэффициент динамической вязкости масла . плотность стали , касторового масла .

Дано: d = 1 мм = 1, v = 0,185 см/с = 1,85, , .

Найти: 

Решение. На шарик действует сила тяжести m, сила Архимеда и сила сопротивления ( рис.4)

 

 

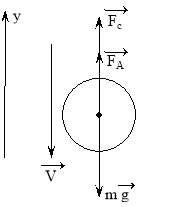
Ускорение шарика равно нулю, и согласно второму закону Ньютона

m++= 0.

Проецируя на вертикальную ось у, имеем

-mg + FA + FC = 0.                                                                                                             ( 15 )

Масса шарика m=gc V, где V – его объём. Сила Архимеда FA = gкq V, а сила сопротивления согласно формуле Стакса Fc =, где - динамическая вязкость, - радиус шарика,

- его скорость. Уравнение ( 15 ) принимает вид – gcqV + gкqV + = 0,

= ( gc-gк) qV.

Так как , а V = , где d – диаметр шарика, то

3,    3,

откуда  динамическая вязкость

.

Проверка размерности .

Подставляем данные:

.

Ответ: 2,27 Пас.