Примеры решенных задач по физике - контрольная 13

4 вариант

2.3.Материальная точка массой m=1,4 кг совершает гармонические колебания. В некоторый момент времени t =3,2 с полная энергия Е=0,4Дж, смещение точки в этот момент равно х=0,1 м. Период колебаний Т=1с. Написать уравнение этих колебаний.

Дано:  m=1,4 кг t =3,2 с Е=0,4Дж х=0,1 м Т=1с

x(t) - ?

            Решение:

Запишем уравнение гармонического колебания: , (1) где А – амплитуда колебаний, - собственная частота колебаний, φ₀ – начальная фаза колебаний.

Тогда уравнения скорости и ускорения колеблющейся точки будут иметь следующий вид:

,

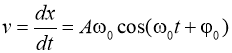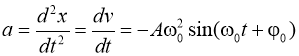
Полная энергия колебания складывается из кинетической и потенциальной энергии и равна максимальной кинетической или максимальной потенциальной энергии: .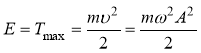

Из этого выражения найдем амплитуду колебания: 

.

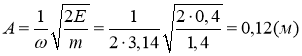Из уравнения (1) можно определить начальную фазу колебаний:  

  

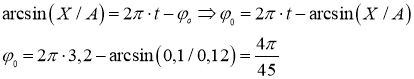
Тогда уравнение колебаний материальной точки будет иметь вид:

 

Ответ:

 

 

 

 

 

3.3.В сосуде объемом V, находится газ при температуре Т=20⁰ С и давлении Р=0,2 МПа. Плотность газа ρ=0,33 кг/м³. Определить число молекул этого газа и что это за газ.

Дано:  Т=200 С=293 К Р=0,2 МПа=2·105 Па ρ=0,33 кг/м3

µ- ?  N- ?

            Решение:

Запишем уравнение Менделеева-Клайперона

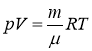, где R=8,31Дж/моль·К – газовая постоянная.

преобразуем его к виду

,

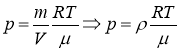отсюда выразим молярную массу газа

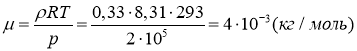
Молярную массу 4 г/моль имеет гелий.

Основное уравнение состояния газа имеет вид: ,

где k=1,38·10^-23 Дж/К – постоянная Больцмана,  - концентрация газа.

Тогда

Отсюда в 1 м³ газа будет

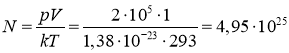 молекул.

 

Ответ: гелий;  N=4,95·10²⁵ молекул.

 

 

4.3.Определить внутреннюю  энергию смеси газов, содержащей υ₁=0,5 молей одноатомного газа, N₂=2·10²³ молекул двухатомного газа и N₃=4·10²³ молекул трехатомного газа. Найдите также энергию вращательного движения всех молекул газа, если энергия двухатомного газа равна ε₂=6·10^-21Дж.

Дано:  υ1=0,5 моль i1=3 N2=2·1023 i2=5 N3=4·1023 i3=6 ε2=6·10-21Дж

ε1 - ?   ε3 -? Uсм - ?

            Решение:

Полная кинетическая энергия движения одной молекулы газа вычисляется по формуле   (1)

где k=1,38·10^-23 Дж/К – постоянная Больцмана; T - термодинамическая температура; где i = 5 – число степеней свободы для двух атомного газа.

Поступательному движению приписывается три (i = 3), а вращательному две (i= 2) степени свободы. Тогда энергия одной молекулы:

.

Из (1) найдем температуру газов:

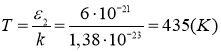
Внутренняя энергия по определению равна:

, где R=8,31Дж/моль·К – газовая постоянная

Вычислим количество вещества 2 и 3 газов по формуле:

;

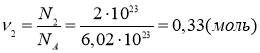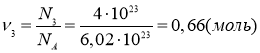
где N_A=6,02·10²³ моль^-1 – постоянная Авогадро

Тогда внутренняя энергия смеси газов будет равна:

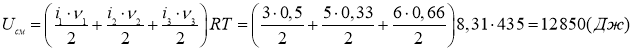Энергия вращательного движения первого газа, газ одноатомный i=3, поэтому

Энергия вращательного движения третьего газа, газ трехатомный i=6, поэтому

Ответ: U_см=12,85 к Дж; ε₁=0; ε₃=9·10^-21Дж .

 

5.3.При изменении состояния газа от Р₁=0,3 МПа, V₁=3л до давления Р₂=0,15 МПа и объема V₂ при изотермическом процессе. Определить работу газа и его конечный объем.

Дано:  Р1=0,3 МПа=3·105 Па V1=3л=3·10-3 м3 Р2=0,15 МПа=1,5·105 Па T=const

V2 - ?  А - ?

            Решение:

При изотермическом процессе T=const, для определения конечного объема воспользуемся законом Бойля-Мариотта:

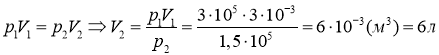 Работа в термодинамике по определению равна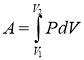  

Выразим давление газа из уравнения Менделеева- Клайперона

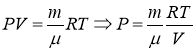 и подставим в формулу работы, получим

 

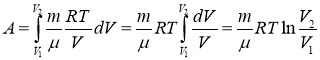
Или с учетом уравнения Менделеева- Клайперона, получим

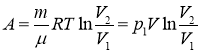
Т.к. процесс изотермический, то по закону Бойля Мариотта

           

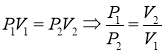
Тогда 

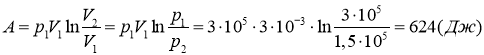
Ответ: V₂ =6 л;  А=624 Дж.

 

6.3.Пластина, изображенная нарисунке, может вращаться вокруг оси ОО^/, проходящей на расстоянии r от левого края пластиы. Вычислить момент инерции пластины относительно этой оси, «разделив» пластину на 10 одинаковых частей одинаковой ширины. Каждую часть принять за материальную точку. Общая ширина пластины 2 м. Поверхностная плотность пластины 2 кг/м². Размеры пластины: а₁=0,2 м; h₁=0,3 м; h₂=0,5 м. На расстояниях х₂=0,6 м и х₃=0,8 м от левого края пластины, перпендикулярно к ней приложена сила F₃= - 2 Н.Положительное направление сил от нас. Найти угловое ускорение пластины.

Дано:  ℓ=2 м σ=2 кг/м2 а1=0,2 м h1=0,3 м h2=0,5 м х2=0,6 м х3=0,8 м F3= - 2 Н

J - ?  ε - ?

            Решение:

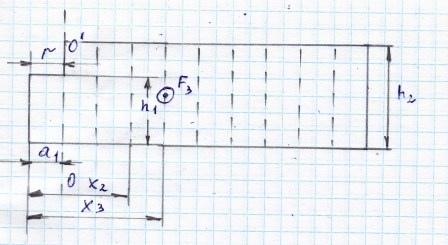
Перерисуем  чертеж с учетом указанных в условии размеров и разобьем  на 10 частей одинаковой ширины, обозначим точки приложения сил. Знак силы F₃ отрицательный, поэтому она направлена к  нам.

Очевидно,  ширина каждой части d = 2/10 = 0,2 м. Масса каждой  части равна её площади, умноженной на поверхностную  плотность, а площадь, в  свою очередь, равна ширине умноженной на высоту:

                    

Заменим  каждую часть материальной точкой,  лежащей в центре  этой части.

Рассчитаем  массы и расстояния до них:

            

            

Расстояния  до масс равны расстояниям от оси до середин соответствующих

 частей.

 

Занесем это все в таблицу:

i	1	2	3	4	5	6	7	8	9	10
mi	0,12	0,2	0,2	0,2	0,2	0,2	0,2	0,2	0,2	0,2
ri	0,1	0,3	0,5	0,7	0,9	1,1	1,3	1,5	1,7	1,9

По определению момент инерции равен  сумме произведений масс всех частей системы на квадраты расстояний от них  до оси вращения:

                  

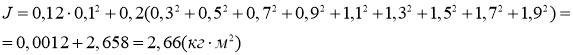
Согласно  основному закону динамики вращательного движения, полный момент сил действующий  на систему равен произведению  момента инерции системы на угловое ускорение:

               , отсюда

По определению, момент силы  равен произведению силы на её  плечо:

         

Отсюда угловое ускорение:

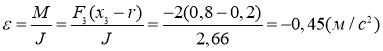
Знак минус  указывает, что вектор углового  ускорения направлен вниз.

 

Ответ: J =2,66 кг·м²;  ε=-0,45 м/с²

 

9.3.На вал радиусом R=0,2 м намотан шнур с грузом массы m=3 кг. Груз падает с высоты h c ускорением а и достигает скорости  v. Момент трения в подшипниках вала М_тр=0,2 Н·м, натяжение шнура F_н. Момент инерции вала J=0,07 кг·м². Найти ускорение груза.

Дано:  m=3 кг R=0,2 м Мтр=0,2 Н·м J=0,07 кг·м2

а - ?

            Решение:

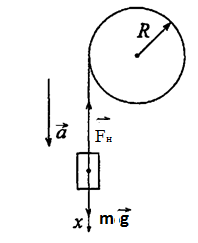
Линейное ускорение а груза  равно тангенциальному ускорению точек вала, лежащих на его поверхности,

и связано с угловым ускорением  вала соотношением:

,                                              (1)

Вращающий момент вала выражается основным уравнением динамики вращающегося тела:

,                                                    (2)

где М — вращающий момент, действующий на вал; J — момент инерции вала.

Присутствие М_тр влияет на ускорение тела и это надо учитывать. Считая момент силы трения не зависящим от скорости вращения, можно записать

Вращающий момент М, действующий на вал, равен произведению силы натяжения  шнура F_н на радиус вала: М= F_н R.

Силу натяжения шнура найдем из следующих соображений. На гирю действуют две силы: сила тяжести , направленная вниз, и сила натяжения F_н шнура, направленная вверх. Равнодействующая этих сил вызывает равноускоренное движение гири.

 По второму закону Ньютона, проекция этих сил на ось ох:

            mg – F_н =ma, откуда F_н =m(g – а).

Таким образом, вращающий момент M=m(g—а)R. (3)

Подставим в это выражение (1),(2) и (3) получим

 

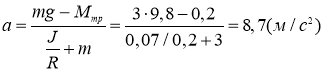
Ответ: а=8,7 м/с².

 

 

10.3.На краю платформы, диск массой m₁ и радиусом R=3 м, стоит человек массой m₂. Платформа вращается с угловой скоростью ω₁=4 об/мин. Когда человек переходит ближе, на расстояние r= 1,5 м от центра, она начинает вращаться с угловой скоростью ω₂=8 об/мин. Момент иннерции платформы J=250 кг·м². Человека можно принять за материальную точку. Найти массу человека.

Дано:  R=3 м ω1=4 об/мин=2/15 об/с r= 1,5 м ω2=8 об/мин=4/15 об/с J=250 кг·м2

m2- ?

            Решение:

 

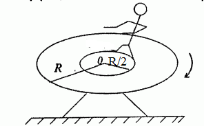
Воспользуемся законом сохранения момента импульса:

                  

Где - момент инерции сплошного диска радиусом R и массой М,

ω₁ – начальная частота вращения  человека с диском, находящихся на краю платформы.

 ω₂ – частота вращения, после перехода  человека ближе к центру. Момент инерции человека , т.к. он стоял на расстоянии R от оси вращения и по условию его можно считать материальной точкой.

 - момент инерции человека, перешедшего ближе к центру на расстояние r = R/2 (см рис).

Тогда

,

 откуда искомая величина равна

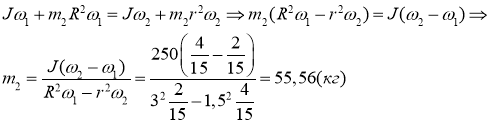
Ответ: m₂=55,56 кг.