Примеры решенных задач по физике - контрольная 12

1.15.Две материальные точки движутся согласно уравнениям: : x₁=A₁t+B₁t²+C₁t³; x₂=A₂t+B₂t²+C₂t³, где А₁=4 м/с, В₁=8 м/с², С₁=-16 м/с³; А₂=2 м/с, В₂=-4 м/с², С₂=1 м/с³. Найти координаты и скорости точек в тот момент, когда ускорения этих точек будут одинаковы.

Дано:

x₁=A₁t+B₁t²+C₁t³

x₂=A₂t+B₂t²+C₂t³

А₁=4 м/с

В₁=8 м/с²

С₁=-16 м/с³

А₂=2 м/с

В₂= - 4 м/с²

С₂=1 м/с³

а₁=а₂

х1– ? х2– ?

v1 -?

Решение:

Скорость это первая производная от координаты по времени

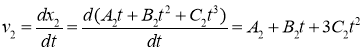
Ускорение это производная от скорости по времени

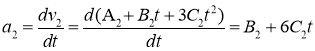
По условию задачи а₁=а_2, тогда

Приравняем правые части этих выражений и выразим время

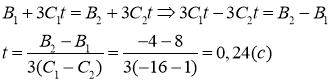
Найдем скорости тел в этот момент времени:

Найдем координаты точек:

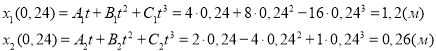
Ответ: v₁=5,18 м/с; v₂=0,25 м/с; х₁=1,2 м; х₂=0,26 м.

2.12.Шарик массой m=10 г ударился о стенку и отскочил от нее со скоростью v=15 м/с, направленной под углом β=60⁰ к поверхности стены. Определить изменение импульса шарика. Удар считать абсолютно упругим.

Дано:

m=** г=0,01 кг

v=15 м/с

β=60⁰

∆р - ?

Решение:

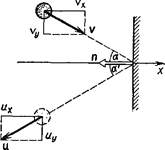
Сначала проанализируем условие задачи. Стенка неподвижна, поэтому система отсчета, связанная с ней, будет инерциальной. Удар о стенку упругий; следовательно, можно воспользоваться законом сохранения механической энергии. Из него, учитывая, что масса стенки много больше массы шара, следует равенство модулей скоростей шара || до и || после удара.

Покажем, что угол ' отражения шара от стенки равен углу падения шара. Спроецируем векторы и на координатные оси Ох и Оу (рис.1). Так как стенка гладкая, то . Учитывая, кроме того, что ||=||, получим а отсюда следует равенство углов падения и отражения ('=).

Для нашего случая этот закон можно записать в виде:

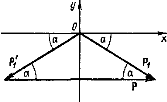где р и р^/– импульсы шара до и после удара . Отсюда импульс, полученный стенкой,

Из рис.2 видно, что вектор сонаправлен с осью Ох и его модуль . Подставив сюда выражение импульса p₁=mv, получим

Заметим, что угол α=90-β

Произведем вычисления:

Ответ: ∆р=0,26 кг.м/с

3.9.Шар массой массой m₁, летящий со скоростью v=10 м/с ударяет о неподвижный шар массой m₂. Удар прямой, не упругий. Определить скорость u шаров после удара, а также долю ω кинетической энергии летящего шара, израсходованную на увеличение внутренней энергии этих шаров. Рассмотреть два случая: 1) m₁=1 кг, m₂=4 кг; 2) m₁=4 кг, m₂=1 кг.

Дано:

v=10 м/с

1) m₁=1 кг, m₂=4 кг;

2) m₁=4 кг, m₂=1 кг

u - ? ω - ?

Решение:

Долю энергии , переданной первым шаром второму, можно найти как

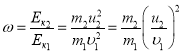, (1)

где Е_к₁ – кинетическая энергия первого шара до удара; Е_к₂ и u₂ – кинетическая энергия и скорость второго шара после удара.

По закону сохранения импульса

m₁₁ = m₁u₁ + m₂u₂, (2)

где u₁ – скорость первого шара после удара.

По закону сохранения механической энергии

(3)

Решая совместно уравнения (2) и (3), найдем скорость

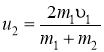(4)

Подставим выражение (4) в (1), сократим на ₁ и m₁ и получим

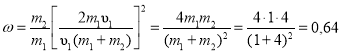Во втором случае:

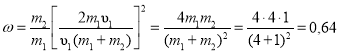
Скорость шаров после удара вычислим по формуле (4):

Во втором случае:

Ответ:1) u =4 м/с; ω=0,64;2) u= 8 м/с; ω=0,64

4.6.Определить момент инерции системы из 3-х стержней (рис) относительно оси, проходящей через центр масс системы параллельно стержням b. Размеры стержней: а=40 см, b=70 см, линейная плотность τ=2 кг/м.

Дано:

а=40 см=0,4 м

b=70 см=0,7 м

τ=2 кг/м

J - ?

Решение:

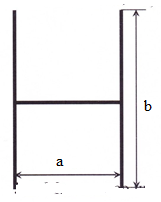
В силу аддитивности, момент инерции данной системы равен сумме моментов инерции:

J = J₁+J₂+J₃. (1)

По условию задачи, ось вращения проходит через центр масс системы параллельно стержням b, значит он проходит через середину стержня а. Линей ная плотность по определению равна

По теореме Штейнера момент инерции стержня

, где - момент инерции стержня относительно оси, проходящей через середину стержня; с – расстояние от середины стержня до оси вращения. Тогда момент инерции стежня а будет равен:

Моменты инерций стержней b, одинаковы, т.к. их масса и расстояние от оси вращения тоже одинаковы. Момент инерции такого стержня можно найти по формуле:

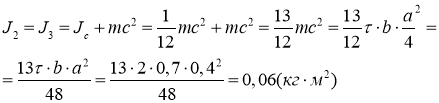
Момент инерции системы:

J = J₁+J₂+J₃=0,01+0,06+0,06=0,13 (кг·м²)

Ответ: J =0,13 кг·м².

5.3. Маховик со шкивом радиусом R=20 см насажен на неподвижную горизонтальную ось. На шкив намотан шнур, к которому привяхан груз массой 5 кг.Определить момент инерции маховика со шкивом, если за две секунды после начала движения груз опустился на 1,2 м.

Дано:

R=20 см=0,2 м

m=5 кг

t=2 c

S=1,2 м

J- ?

Решение:

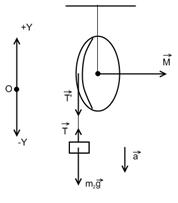
На груз действует сила тяжести mg и сила натяжения шнура Т. Уравнение поступательного движения груза по второму закону Ньютона

Проекция на ось Y:

Сила натяжения нити

По определению момент силы

Откуда момент инерции барабана

Используя связь линейного и углового ускорения, находим

Тогда момент инерции барабана

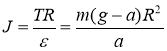(1)

Путь, пройденный грузом, найдём по формуле равноускоренного движения, учтя, что начальная скорость равна нулю:

, отсюда ускорения груза

Подставим в (1), получим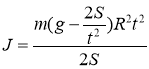

Подставим числовые значения, получим:

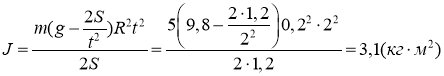
Ответ: J=3,1 кг·м².

6.25.Продолжительность суток на некоторой планете составляла 50 часов. В процеесе эволюции момент инерции планеты увеличился на 5%. Какой стала продолжительность суток на планете? Как изменилась ее кинетическая энергия?

Дано:

Т₁=50 час=18·10⁴ с

J₂=J₁+0,05J₁=1,05 J₁

T₂ - ?

Решение:

Так как шар вращается по инерции, то момент внешних сил относительно оси вращения z, совпадающий с геометрической осью шара, равен нулю. При этом условии момент импульса L_z остается постоянным:

L_z = J_z = const, или

Угловая скорость связана с периодом соотношением: (1)

Отсюда получим

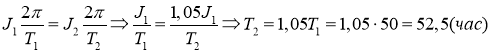
Кинетическая энергия тела вращения вычисляется по формуле:

E_k = .

Запишем это выражение для двух случаев, учитывая (1)

Поделим второе на первое

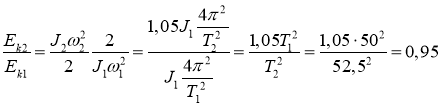
Ответ: Т₂=52,5 час; кинетическая энергия уменьшилась.

7.22.В днище судна на глубине h=1 м ниже ватерлинии образовалась пробоина площадью S=0,2м². Какая масса воды ежесекундно заливается в трюм судна?

Дано:

h=1 м

S=0,2м²

t=1c

ρ=10³ кг/м³

m - ?

Решение:

Объем воды, проникающей внутрь корабля, определяется по формуле:

, где - площадь пробоины, v – скорость истечения воды, которую определим по формуле Торричелли:

Подставим эти выражения в первоначальную формулу, получим

Массу вычислим по формуле:

Подставим числовые значения, получим

Ответ: ежесекундно заливается 885 кг.

8.19.Определить напряженность и потенциал электрического поля в центре квадрата, в вершинах которого находятся заряды Q₁= - 2 нКл, Q₂= 1 нКл;

Q₃= 4 нКл; Q₄= 2 нКл, сторона квадрата а=5 см. Определить также энергию взаимодействия данной системы зарядов.

Дано:

Q₁= - 2 нКл= - 2·10^-9 Кл

Q₂=1 нКл = 10^-9Кл

Q₃=4нКл=4·10^-9Кл

Q₄=2нКл=2·10^-9Кл

а=5 см=5·10^-2м

Е_А-? φ - ? Е - ?

Решение:

Изобразим линии напряженности, получаемые от зарядов в квадрате.

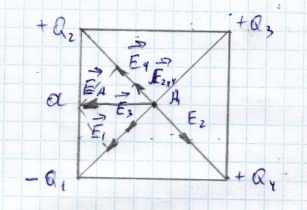
$C:\Users\1\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\IMG_20191212_0001.jpg$

По принципу суперпозиции вектор напряженности электростатического поля равен векторной сумме напряженностей, созданных каждым зарядом в отдельности .

Заряды 1 и 3 разные по знаку, поэтому модуль напряженности от них в точке А будет равна нулю.

Заряды 4 и 2 разные по величине, но одинаковых знаков, поэтому модуль их суммарной напряженности равен

Модуль вектора напряженности точечного заряда q вычисляется по формуле

, где к=9·10⁹Н·м²/Кл, r – расстояние от точки А до заряда, в нашем случае

Поэтому

Результирующая напряженность в центре квадрата (см рис.) равна:

Ответ: Е_А=50,4 кВ/м

9.16.Электрон, пройдя в плоском конденсаторе путь от одной пластины до другой, приобрел скорость v=10⁶ м/с. Определить напряженность поля внутри конденсатора, если расстояние между пластинами d=3 см.

Дано:

v = 10⁶ м/с

d = 3 см = 3·10^-2 м

m_е = 9,1·10⁻³¹ кг

е = 1,6·10⁻¹⁹ Кл

Е - ?

Решение:

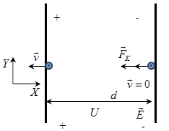
Для электрона 2-й закон Ньютона запишется в виде

Проекция на ось Х

Х:

Под действием силы Кулона электрон приобретет ускорение

Сила Кулона

Связь напряженности и разности потенциалов

Тогда

Расстояние, пройденное электроном, найдем из кинематического выражения:

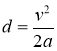отсюда ускорение электрона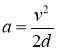

Тогда напряженность поля

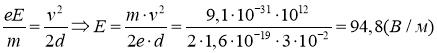
Ответ: Е=94,8 В/м.

10.13.Между двумя населенными пунктами протянут медный провод длиной ℓ=1000 м и сечением S=10 мм². По нему течет ток силой I=45 А. Считая, что концентрация свободных электронов меди n=10²⁹ м³ найдите время, за которое электроны преодолеют это расстояние.

Дано:

ℓ=1000 м

S=10 мм²=10^-5м²

I=45 А

n=10²⁹ м³

t - ?

Решение

За промежуток времени через поперечное сечение проводника протечет заряд:

(1)

где S- площадь поперечного сечения проводника,

v- средняя скорость направленного движения свободных электронов в проводнике (скорость дрейфа), е=1,6∙10^-19Кл – заряд электрона, n – концентрация зарядов

По определению , тогда выражение (1) преобразуется к виду:

Согласно определнию сила тока .

Тогда получаем

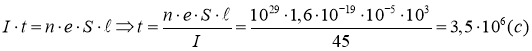
Ответ: t=40,5 суток.

11.15.Протон, прошедший ускоряющую разность потенциалов U =600В, влетел в однородное магнитное поле с индукцией В=0,3 Тл и начал двигаться по окружности. Вычислить ее радиус.

Дано:

q=1,6·10^-19 Кл

m=1,67·10^-27 кг

U=600 В

В=0,3 Тл

R - ?

Решение

Радиус кривизны траектории частицы определим, исходя из следующих соображений: на движущуюся в магнитном поле частицу действует сила Лоренца (действием силы тяжести можно пренебречь). Сила Лоренца перпендикулярна вектору скорости и, следовательно, сообщает частице нормальное (центростремительное) ускорение: :

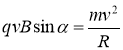(1), где е- заряд, v- скорость, m- масса; В- индукция магнитного поля; R- радиус кривизны траектории; - угол между направлением вектора скорости и вектором (электрон движется по окружности значит α=90⁰)

Из формулы (1) найдем: 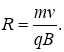(2)

Входящий в равенство (2) импульс mv может быть выражен через кинетическую энергию частицы: (3)

Но кинетическая энергия частицы, проходящая ускоряющую разность потенциалов U, определяется равенством:

Подставив это выражение в формулу (3), получим:

Подставив найденные выражения В и mv в формулу (2),найдем

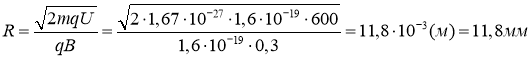
Ответ: R=11,8 мм

12.12. Три длинных прямых провода с током лежат в одной плоскости (рис). Расстояние между соседними проводами одинаково и равно а=4см. Величины токов указаны в таблице (I₁=4А; I₂= - 2А; I₃=3А).Знаком минус обозначен ток, противоположный по направлению токам, указанный на рисунке. Вычислить силу F, действующую на отрезок длиной 1 м провода, номер которого указан в правом столбце таблицы (провод №1)

Дано:

а=4см=4·10^-2 м

I₁=4А

I₂= - 2А

I₃=3А

ℓ=1м

F/ℓ - ?

Решение:

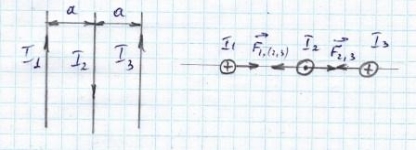
$C:\Users\1\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\IMG_20191212_0001.jpg$

Взаимодействие трех проводников, по которым текут токи, осуществляется через магнитное поле. Каждый ток создает магнитное поле, которое действует на другой проводник. По условию задачи I₁ и I₃ текут в одном направлении, а ток I₂ – в другом.

Провода с током I₂ и I₃ притягиваются друг к другу с силой F_2.3 (см рис)

Вычислим силу F_2,3, с которой магнитное поле, созданное током I₂,

действует на проводник с током I₃.

Согласно закону Ампера, на каждый элемент второго проводника с током I₂ и длиной dℓ₂ действует в магнитном поле сила

Модуль магнитной индукции B₂ определяется соотношением

Т.к. вектор В₂ перпендикулярен отрезку провода dℓ₂, то и тогда

(2)

Проинтегрировав это выражение, получим

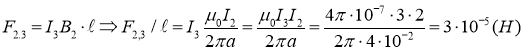
Проводники 1 и 2 тоже притягиваются друг к другу с силой

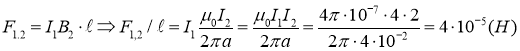
Проводники 1 и 3 отталкиваются друг от друга с силой:

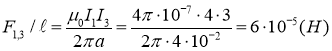
На первый провод со стороны других проводов действует сила равная:

Ответ: F=70 мкН

13.9.Магнитное поле создается четырьмя длинными прямыми параллельными проводниками с током, оси которых находятся в вершинах квадрата, лежащего в плоскости, перпендикулярной этим осям. Сторона квадрата а=4 см. Определите величину и направление магнитной индукции в точке О (центр квадрата), если I₁=3А; I₂= - 1А; I₃=4А; I₄=2А. Знаком минус указаны токи, противоположные указанным на рисунке.

Дано:

а=4см=4·10^-2м

I₁=3А

I₂= - 1А

I₃=4А

I₄=2А

В_О-?

Решение:

Определим направление вектора магнитной индукции (по правилу буравчика), созданных каждым током в отдельности:

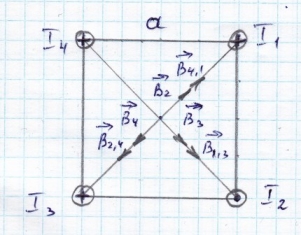
$C:\Users\1\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\IMG_20191212_0001.jpg$

По принципу суперпозиции результирующий вектор магнитной индукции равен

Так как расстояние от проводников до точки О одинаковые, то r=a√2/2.

Направления и совпадают, следовательно В_1,3= В₁+ В₃

Магнитное поле прямого тока

Вектора и направлены вдоль одной прямой, но в противоположные стороны, поэтому

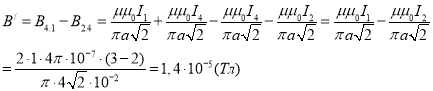
Результирующая индукция в точке О найдем по теореме косинусов:

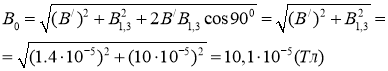
Ответ: В₀=101 мкТл.

14.6.Прямой провод длиной ℓ=40 см движется в однородном магнитном поле со скоростью v=5 м/с перпендикулярно линиям магнитной индукции. Разность потенциалов между концами провода при этом U=0,6 В. Вычислите индукцию магнитного поля.

Дано:

l = 40 см=0,4м

υ = 5 м/с

U=0,6 В

В - ?

Решение:

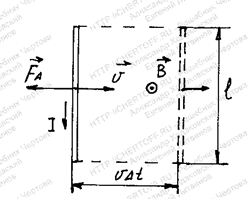
При движении проводника с постоянной скоростью за время ∆t им охватывается площадь

При этом в проводнике возникает эдс индукции

Разность потенциалов, возникающая на концах проводника равна

Отсюда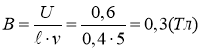

Ответ: В=0,3 Тл

15.3. Найдите частоту света, вырывающего из металла электроны, которые полностью задерживаются разностью потенциалов U=3 В. Фотоэффект начинается при частоте света равной 6·10¹⁴ Гц. Определите работу выхода электронов из металла.

Дано:

U=3 В

υ_кр=6·10¹⁴ Гц

υ - ? А -?

Решение:

Красная граница фотоэффекта – максимальная длина волны, при которой возможен фотоэффект. Согласно уравнению Эйнштейна для внешнего фотоэффекта

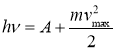(1)

где h=6,62·10^-34Дж· с – постоянная Планка,

Максимальная длина волны, при которой возможен фотоэффект, отвечает нулевой кинетической энергии фотоэлектронов, т.е. работу выхода можно выразить следующим образом:

принимая во внимание, что по условию задачи

где е=1,6·10^-19 Кл – величина элементарного заряда, уравнение для фотоэффекта запишется , отсюда частота падающего света

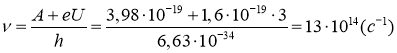
Ответ: υ=13·10¹⁴ Гц; А=2,49 эВ.

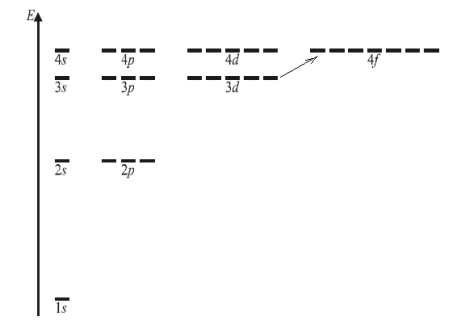
16.25.В атоме водорода электрон первоначально находился в состоянии 3d. Определите, какая энергия выделяется или поглощается атомом при переходе электрона в другое конечное состояние - 4f. Укажите, какой процесс (выделение или поглощение энергии) происходит при таком переходе. Покажите переход на диаграмме состояний электрона в атоме водорода.

Дано:

- ?

Решение:

Энергетические уровни в атоме Бора, соответствующие разным значениям квантовых чисел n и ℓ

Согласно квантовой теории, квантовое состояние электрона в атоме может быть детально описано с помощью трех квантовых чисел: n, l и m, которые позволяют рассчитать для каждого квантового состояния энергию Wn.

Значению квантового числа n = 3 в атоме водорода отвечают состояния 3s, 3p и 3d с одинаковой энергией W₃, значению квантового числа n = 4 в атоме водорода отвечают состояния 4s, 4p, 4d и 4f с одинаковой энергией W₄.

Поэтому при переходе электрона на более высокий уровень, энергия поглощается.

17.22.Определите радиус воздушного шар-зонда при температуре t₀=2⁰С, если для его накачивания использовали 5 баллонов водорода емкостью V=20 л каждый, запоненных при температуре t=27⁰С до давления р=1 МПа. Давление в шар-зонде р₀=100 кПа.

Дано:

t₀=2⁰С=275К

р₀=100 кПа=10⁵ Па

V=20 л=2·10^-2 м³

n=5

t=27⁰С=300 К

р=1 МПа=10⁶ Па

R₀ - ?

Решение:

Запишем уравнение состояния газа и найдем объем шар-зонда:

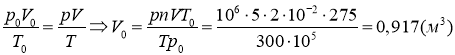Объем шара определяется по формуле:

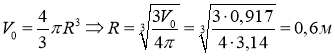
Ответ: R₀=60 см

18.19.Найдите среднюю энергию вращательного движения одной молекулы углекислого газа при температуре t=37⁰С, а также внутренню энергию 2 молей этого газа.

Дано:

υ= 2 моль

Т = 37⁰С=310К

<ε> - ? U - ?

Решение:

Считаем водород идеальным газом. Молекула углекислого газа – трехатомная. Связь между атомами считаем жесткой, тогда число степеней свободы молекулы водорода равно 6. В среднем на одну степень свободы приходится энергия: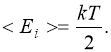 где k=1,38·10^-23 Дж/К – постоянная Больцмана

Поступательному движению приписывается три (i = 3), а вращательному две (i= 3) степени свободы. Тогда энергия одной молекулы:

По определению внутренняя энергия газа равна ,

Где - молярная изохорная теплоемкость газа, R=8,31Дж/моль·К – газовая постоянная

тогда

Ответ: <ε_вр> =6,4·10^-21 Дж; U=15456,6 Дж.

19.16.6 молей двухатомного газа занимали объем V₁=100 л при давлении р₁=0,15 МПа. Газ был нагрет сначала при постоянном объеме до давления р₂=0,5МПа, а зетем при постоянном давлении до объема V₂=300 л. Найдите количество теплоты, переданного газу. Постройте график процесса.

Дано:

υ=6 моль

i=5

V₁=*** л=0,1м³

р₁=0,15 МПа=1,5·10⁵ Па

р₂=0,5 МПа=5·10⁵ Па

V₂=300 л=0,3м³

Q - ?

Решение:

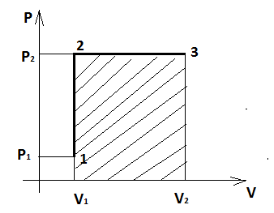
Для начала определим термодинамические параметры (давление, объем и температуру) газа в трех состояниях, между которыми осуществлялся замкнутый термодинамический процесс.

Температуру газа в исходном состоянии определим из уравнения состояния идеального газа:

Отсюда,

Во втором состоянии температура будет равна

Согласно первому началу термодинамики, теплота Q, переданная газу, равна сумме изменения внутренней энергии и работы A:

В изохорном процессе (V = const) газ работы не совершает, A = 0.

Поэтому

Внутреннею энергию найдем по формуле:

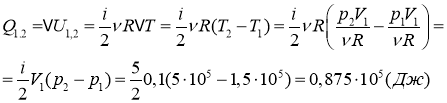
В изобарном процессе (p = const) работа, совершаемая газом, выражается соотношением:

Изменение внутренней энергии при этом переходе:

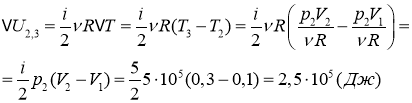
Тогда количество теплоты в этом переходе:

Общее количество теплоты за цикл:

Ответ: Q=437,5 кДж.

20.13.Идеальный газ в цикле Карно совершил работу А=750 Дж, отдав холодильнику количество теплоты Q₂= 3кДж. Найти термический КПД этого цикла. Во сколько раз температура Т₁ нагревателя больше температуры Т₂ холодильника?

Дано:

Q₂=3 кДж=3∙10³Дж

А=750 Дж

η - ? Т₁/Т₂ - ?

Решение:

Воспользуемся теоремой Карно: коэффициент полезного действия (к. п. д.) тепловой машины, работающей по циклу Карно, зависит только от температур нагревателя и холодильника и не зависит от природы рабочего тела и устройства тепловой машины

К. п. д. цикла Карно можно записать также через работу и тепло , переданное рабочему телу от нагревателя: , где

Отсюда , тогда

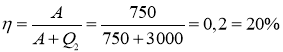(2)

Приравняем (1) и (2) и выразим искомую величину

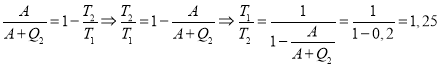
Ответ: η=20%; Т₁/Т₂= 1,25.

21.15.Какие изотопы образуются в цепочке радиоактивных распадов ядер, приведенных в таблице?

Исходное ядро:

Решение:

- в атоме Z- порядковый номер или заряд ядра; А – атомная масса

После β⁻-распада элемент смещается на 1 клетку к концу таблицы Менделеева (заряд ядра увеличивается на единицу), тогда как массовое число ядра при этом не меняется.

Правило смещения Содди для β-распада:

Бетта распад протекает по следующей схеме:

После 2- х бетта распадов получился изотоп висмута

В результате одного α-распада атом смещается на 2 клетки к началу таблицы Менделеева (то есть заряд ядра Z уменьшается на 2), массовое число дочернего ядра уменьшается на 4.

Правило смещения Содди для α-распада:

Альфа-распад протекает по следующей схеме:

После 1 альфа-распада получился изотоп таллия.

Бетта распад протекает по следующей схеме:

По таблице Менделеева определяем, что получившийся элемент, это изотоп свинца

Ответ: изотоп свинца.

22.12.В таблице приведена ядерная реакция . Определите недостающее в записи ядро или частицу и энергию реакции.

Дано:

E - ?

Решение:

Ядерная реакция имеет вид:

- в атоме Z- порядковый номер или заряд ядра; А – атомная масса

По правилу смещения Содди, общее число атомных масс ядер вступивших в реакцию, должно быть равно числу атомных масс ядер после реакции.

До реакции число атомных ядер: А=11+4=15.

После реакции: А=15-1=14

с такой атомной массой может быть ядро изотопа азота

Поэтому реакция будет иметь вид:

Энергию ядерной реакции определим по формуле

E=931m,

где m - изменение массы при реакции, т е разность между массой частиц, вступающих в реакцию, и массой частиц, образовавшихся в результате реакции:

(2)

здесь — масса атома бора,— масса гелия, —масса изотопа азота, — масса атома водорода. Из таблиц находим массы этих атомов и по формуле (2) вычисляем m:

m=(11,00931+4,002602) a.e.м.- (14,00307+1,00783) а.е.м.=0,001012 а.е.м.

Подставим числовое значение m в (1) и вычислим энергию ядерной реакции:

E= 931,5·0,001012 МэВ= 0,94 МэВ.