Пример решения задачи по электротехнике - задача 1
Определить токи и напряжение U43, оставить баланс мощностей, МЭГ определить ток в сопротивлении R8.
Дано : R1=420 Ом ; R2=210 Ом ; R3=160 Ом ; R4=630 Ом ; R5=350 Ом ; R6=530 Ом ; R7=360 Ом ; R8=610 Ом ; E6=100 В ; E8=600 В ; J2=3 A ; J8=5 A.
Найти : токи в ветвях цепи, напряжение U43.
Решение.
Расположим шесть узлов цепи в указанном порядке и в соответствии с вариантом задания соединим их ветвями. ( рис 1).
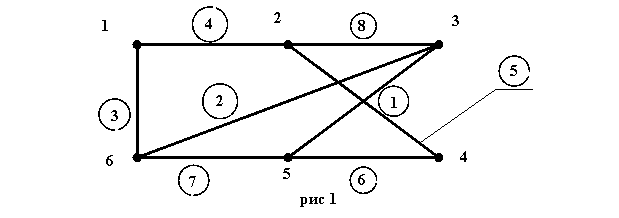
Перерисуем полученный граф схемы, изменив расположение узлов таким образом, чтобы ветви не пересекались. (рис 2).
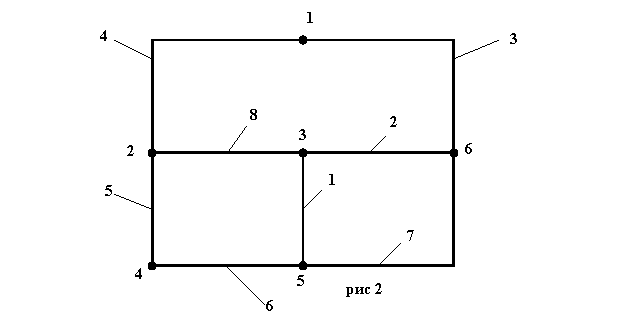
Включим в ветви сопротивления и заданные ЭДС. Источники тока подключим параллельно соответствующим ветвям. (рис 3).
Придадим элементам схемы удобное расположение.
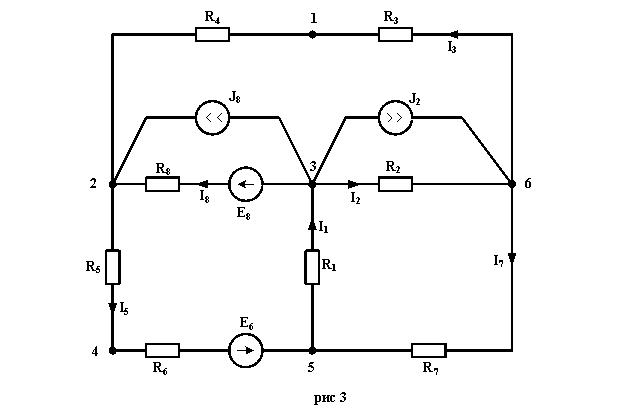
Найдём токи в ветвях цепи методом узловых потенциалов. Примем потенциал точки 6 равным нулю : V6=0. Тогда, для остальных трёх узлов, запишем три уравнения для потенциалов этих узлов.
G22V2-G23V3-G25V5=G23E8-G25E6+J8
-G32V2+G33V3-G35V5= -G32E8-J8-J2
-G52V2-G53V3+G55V5=G52E6
где G22, G33, G55 – собственная проводимость узлов 2, 3 и 5 ; G23=G32, G25=G52, G35=G53 – общая проводимость между узлами соответственно 2 и 3, 2 и 5, 3 и 5.
Найдём эти проводимости.
G22=![]() сим
сим
G33=![]() сим.
сим.
G55=![]() сим.
сим.
G23=G32=![]() сим.
сим.
G25=G52=![]() сим.
сим.
G35=G53=![]() сим.
сим.
Подставляя в составленные уравнения, полученные значения проводимостей и, заданные значения источников ЭДС и тока. Получим систему для определения потенциалов точек схемы.
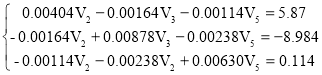
Решим, полученную систему по формулам Крамера.
Δ= 163.33×10-9
163.33×10-9
Δ1= 175.831×10-6
175.831×10-6
Δ2=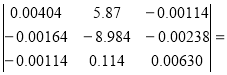 -139.101×10-6
-139.101×10-6
Δ3= -17.777×10-6
-17.777×10-6
Находим потенциалы узловых точек :
V2=![]() 1076.538 В
1076.538 В
V3=![]() -851.656 В
-851.656 В
V5=![]() -108.841 В
-108.841 В
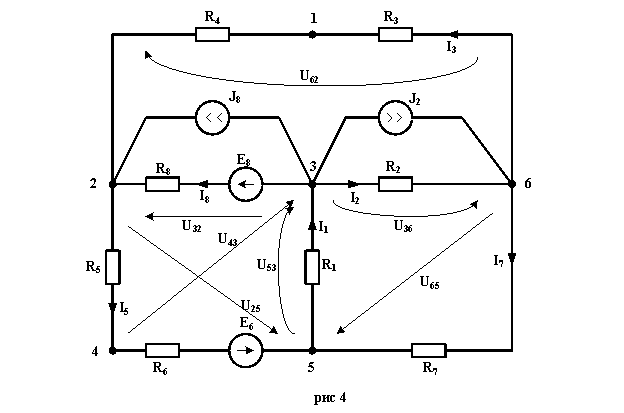
Находим токи в ветвях схемы (рис 4).
I1=U53/R1=(V5-V3)/R1=(-108.841+851.656)/420=1.769 A ;
I2=U36/R2=(V3-V6)/R2=(-851.656-0)/210=-4.056 A
I3=U62/(R3+R4)=(V6-V2)/(R3+R4)=-1076.538/(160+630)=-1.363 A
I5=(E6+U25)/(R5+R6)=(E6+V2-V5)/(R5+R6)=(100+1076.538+108.841)/(350+530)=1.461 A
I7=U65/R7=(V6-V5)/R7=108.841/360=0.302 A
I8=U32/R8=(E8+V3-V2)/R8=(600-851.656-1076.538)/610=-2.177 A
Найдём мощность приёмников :
Pпр=![]() =
=
=1.7692×420+4.0562×210+1.3632×790+1.4612×880+0.3022×360+2.1772×610=11038.9 Вт
Найдём мощность источников :
Pис=E8I8+E6I5+J8(V2-V3)+J2(V6-V3)=
=600×(-2.177)+100×1.461+5×(1076.538+851.656)+3×851.656=11035.8 Вт.
Составляем баланс мощностей :
Pпр=11039 Вт=Pис=11036 Вт
Найдём напряжение U43.
По второму закону Кирхгофа для контура 3543, обходя его в направлении против хода часовой стрелки, запишем :
I5R6+I1R1-U43=E6
Отсюда находим U43 :
U43=I5R6+I1R1-E6=1.461×530+1.769×420-100=1417.31 В.
Определим ток в резисторе R8 методом эквивалентного генератора.
Разомкнём цепь с резистором R8 и найдём э.д.с. и сопротивление Rэк эквивалентного генератора (рис 6). Э.д.с. Eэк эквивалентного генератора равно напряжению U в цепи без ветви с сопротивлением R8. Сопротивление Rэк эквивалентного генератора равно эквивалентному сопротивлению цепи с отключенной ветвью с сопротивлением R8.
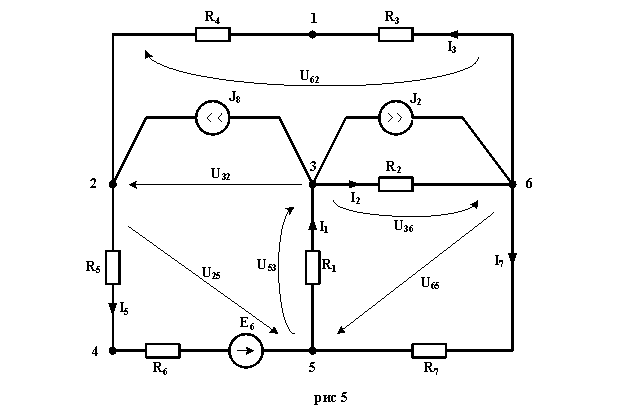
Найдём токи в цепи (рис 5) методом узловых потенциалов.
Примем потенциал точки 2 равным нулю : V2=0. Тогда, для остальных трёх узлов, запишем три уравнения для потенциалов этих узлов.
G33V3-G35V5-G36V6= -J8-J2
-G53V3+G55V5-G56V6= G52E6
-G63V3-G65V5+G66V6=J2
где G33, G55, G66 – собственная проводимость узлов 3, 5 и 6 ; G35=G53, G36=G63, G56=G65 , G52 – общая проводимость между узлами соответственно 3 и 5, 3 и 6, 5 и 6, 5 и 2.
Найдём эти проводимости.
G33=![]() сим
сим
G55=![]() сим.
сим.
G66=![]() сим.
сим.
G35=G53=![]() сим.
сим.
G36=G63=![]() сим.
сим.
G56=G65=![]() сим.
сим.
G52=![]() сим.
сим.
Подставляя в составленные уравнения, полученные значения проводимостей и, заданные значения источников ЭДС и тока. Помощь на экзамене онлайн. Получим систему для определения потенциалов точек схемы.
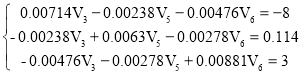
Решим, полученную систему по формулам Крамера.
Δ= 85.476×10-9
85.476×10-9
Δ1=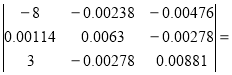 272.345×10-6
272.345×10-6
Δ2=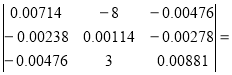 180.025×10-6
180.025×10-6
Δ3=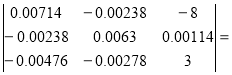 174.847×10-6
174.847×10-6
Находим потенциалы узловых точек :
V3=![]() 3186.216 В
3186.216 В
V5=![]() 2106.147 В
2106.147 В
V6=![]() 2045.568 В
2045.568 В
Находим токи в ветвях схемы (рис 5).
I1=U53/R1=(V5-V3)/R1=(2106.147-3186.216)/420=-2.572 A ;
I2=U36/R2=(V3-V6)/R2=(3186.216-2045.568)/210=5.432 A
I3=U62/(R3+R4)=(V6-V2)/(R3+R4)=2045.568/(160+630)=2.589 A
I5=(E6+U25)/(R5+R6)=(E6+V2-V5)/(R5+R6)=(100-2106.147)/(350+530)=-2.28 A
I7=U65/R7=(V6-V5)/R7=(2045.568-2106.147)/360=-0.168 A
Находим ЭДС эквивалентного генератора (рис 5) :
Eэк=U32=V3-V2=3186.216 В
Находим сопротивление цепи относительно разомкнутых точек. Преобразуем звезду сопротивлений R2, R34, R7 в эквивалентный треугольник (рис 6).

Найдём сопротивления эквивалентного треугольника :
R25=![]() Ом
Ом
R35=R2+R7+![]() Ом.
Ом.
R23=R2+R34+![]() Ом.
Ом.
Находим эквивалентное сопротивление цепи(рис 6) относительно точек 2 и 3 :
R/=![]() Ом.
Ом.
Rэк=![]() Ом.
Ом.
Находим ток через резистор R8 (рис 7) :

I8=![]() A
A
Ответ : I1=1.8 A ; I2=-4.1 A ; I3=-1.4 A ; I5=1.5 A ; I7=0.3 A ; I8=-2.2 A. Знак «минус» в значениях токов I2, I3 и I8 означает, что направления этих токов противоположно показанному на рисунке.
