Пример решения контрольной по электротехнике - 3
Задание 1. Расчет сложной цепи постоянного тока.
Для обобщенной цепи, приведенной в задании, требуется выполнить следующее:
1. Составить расчетную схему электрической цепи.
2. Записать систему уравнений Кирхгофа, необходимых для определения токов во всех ветвях схемы.
3. Выполнить расчет схемы методом контурных токов и найти токи во всех ветвях схемы.
4. Выделить в схеме три сопротивления, включенные по схеме треугольника, и заменить их эквивалентными сопротивлениями по схеме звезда.
5. Рассчитать полученную схему методом узловых напряжений и найти токи в ветвях.
6. Определить ток в сопротивлении 
по методу эквивалентного генератора.
7. Рассчитать напряжение между точками 
и 
схемы.
8. Составить баланс мощностей для исходной схемы.
Дано:
Решение.
1. Схема расчетной цепи в соответствии с заданием представлена на рисунке.
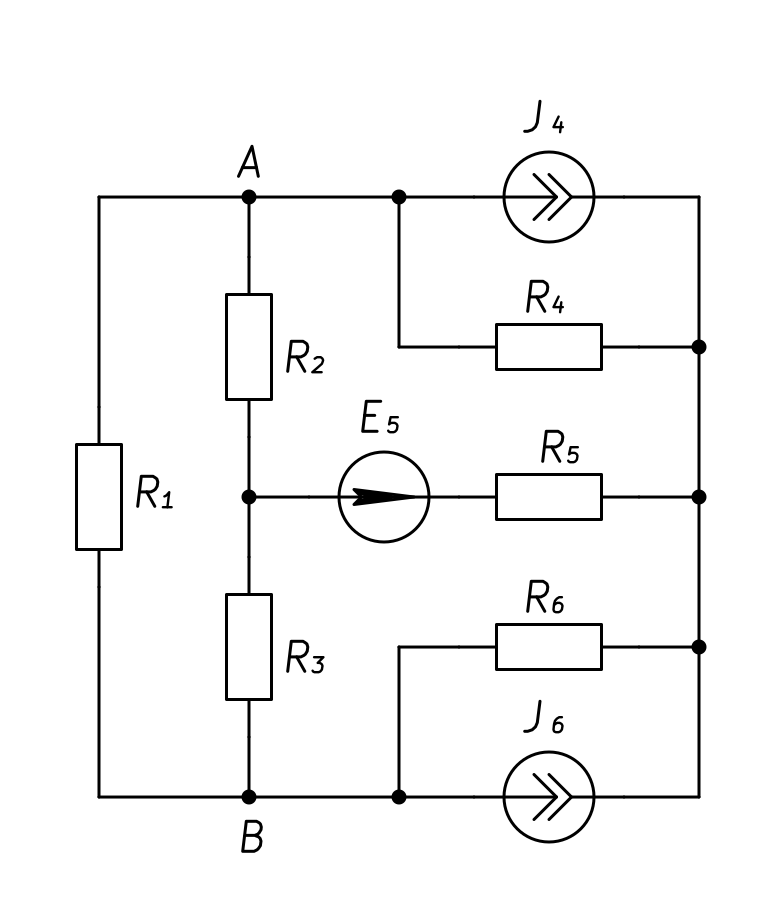
Рисунок 1. Схема электрической цепи в соответствии с заданием
2. Составление на основании законов Кирхгофа системы уравнений для расчета токов во всех ветвях схемы.
Схема расчетной цепи с выбранными для расчета направлениями токов в ветвях, контурными токами и обозначенными узлами представлена на рисунке.
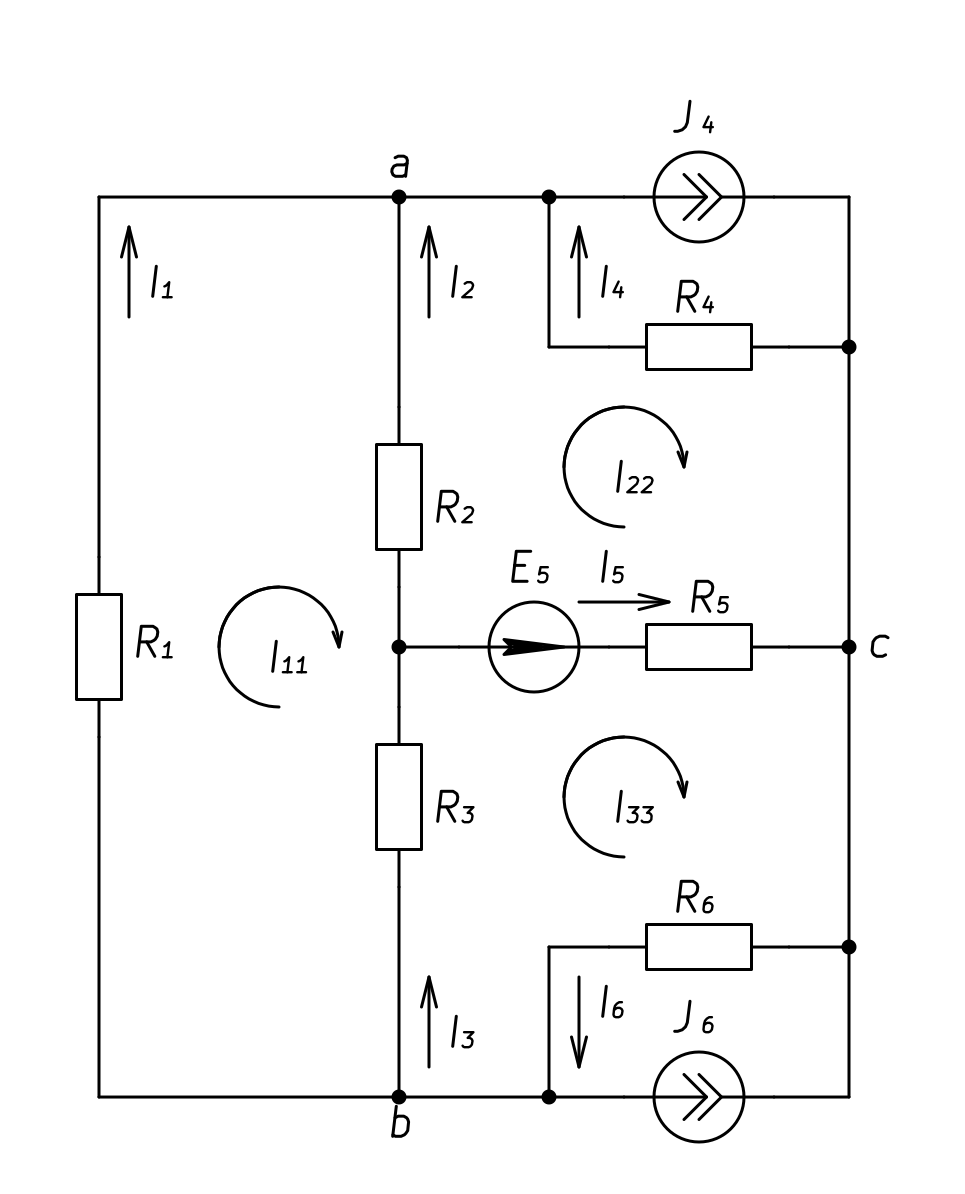
Рисунок 2. Схема расчетной электрической цепи
Цепь содержит четыре узла, и три независимых контура. Поэтому система уравнений по законам Кирхгофа будет содержать шесть уравнений – три уравнения по 
закону и три уравнения по 
закону.
Уравнения по закону Кирхгофа будем составлять для узлов 
, обход контуров при составлении уравнений по закону Кирхгофа будем осуществлять по часовой стрелке.
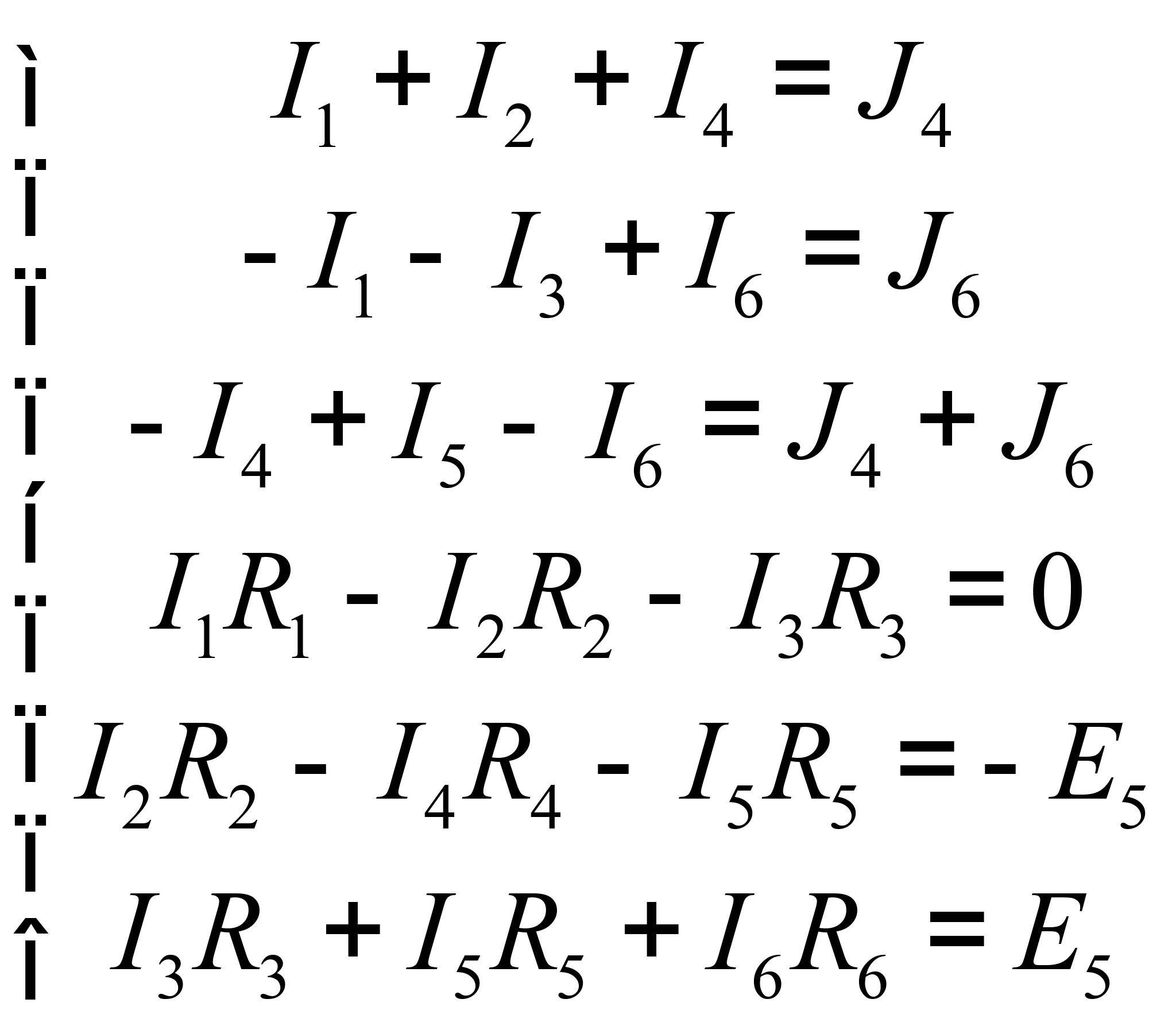
3. Расчет токов во всех ветвях схемы методом контурных токов.
При составлении уравнений по методу контурных токов токи источников 
замыкаются соответственно через резисторы 
. Система уравнений, составленная по методу контурных токов, имеет вид
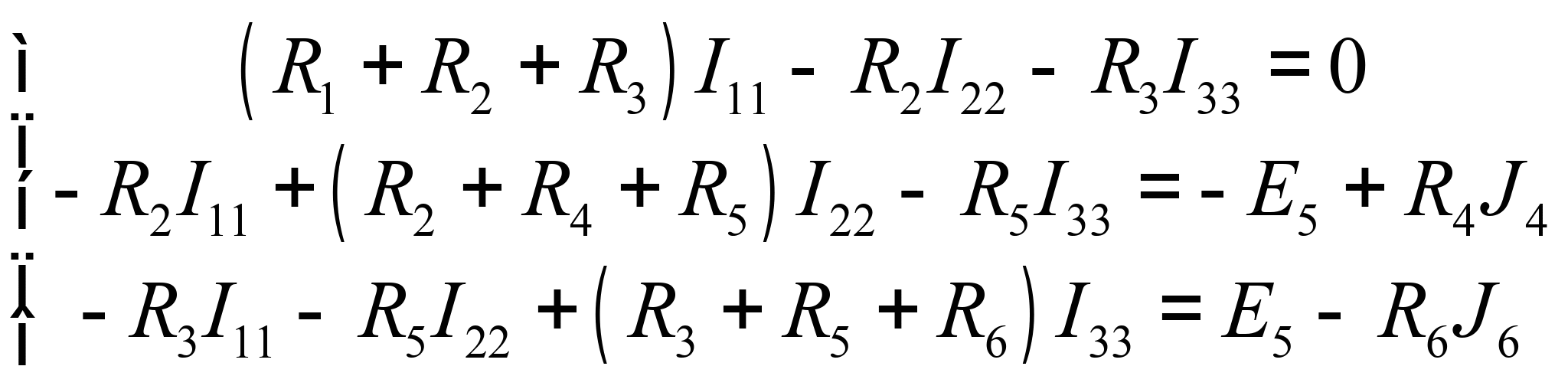
Подставляя числовые значения, получаем
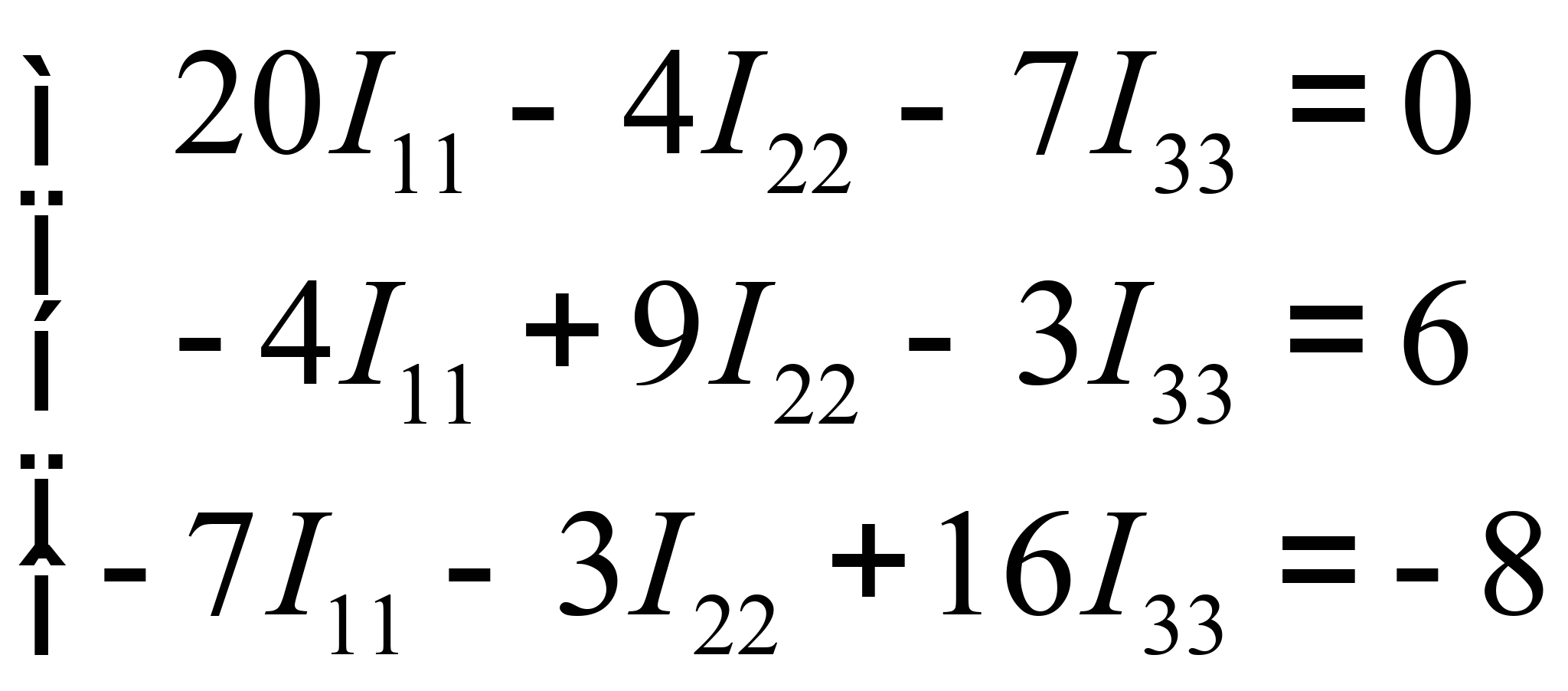
Решая систему, определяем контурные токи
, 
, 
Определяем токи в ветвях цепи:
Отрицательные значения токов означают, что условно положительные направления токов противоположны выбранным для расчета.
4. Замена сопротивлений, включенных по схеме треугольника, эквивалентными сопротивлениями по схеме звезда.
В схеме треугольником включены сопротивления 
. Заменим их эквивалентной звездой 
. Схема преобразованной цепи с обозначенными узлами для расчета методом узловых напряжений приведена на рисунке.
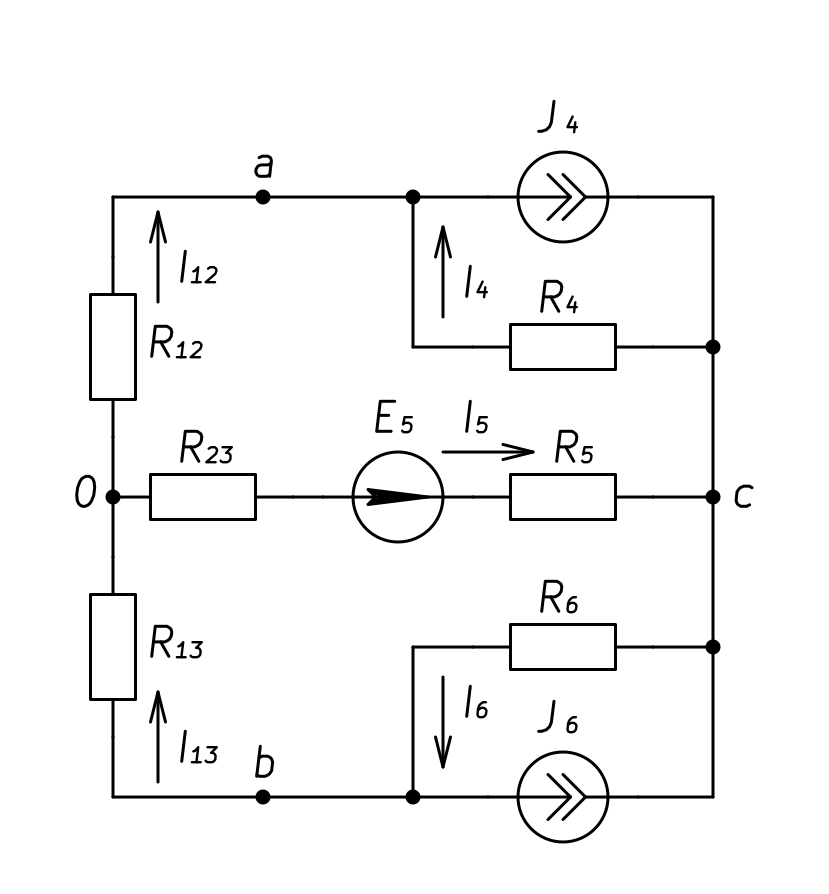
Рисунок 3. Схема расчетной электрической цепи, в которой треугольник сопротивлений заменен эквивалентной звездой
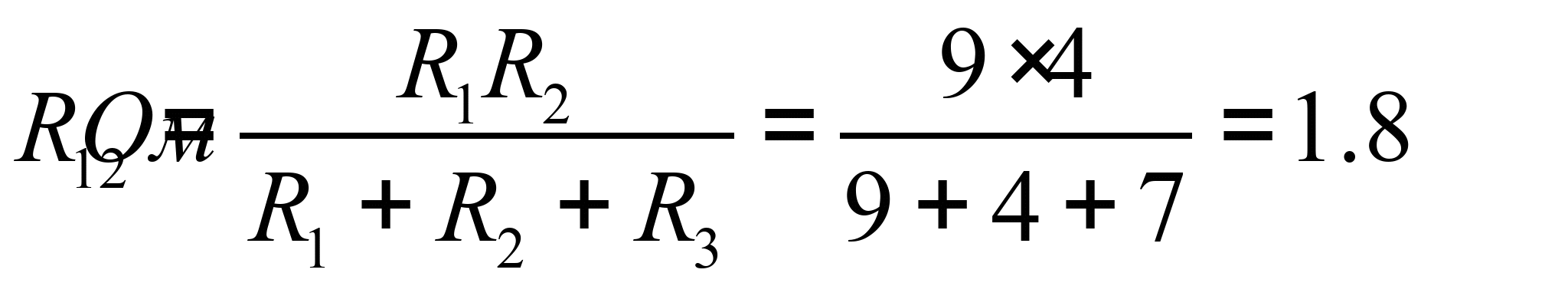
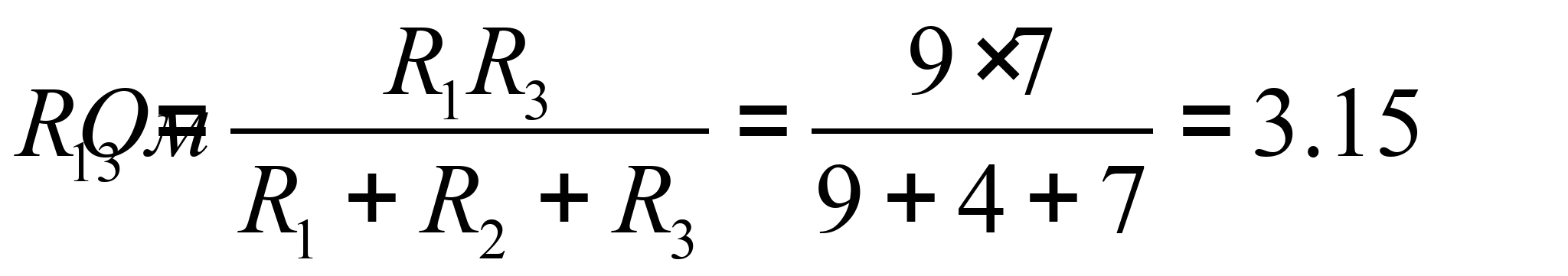
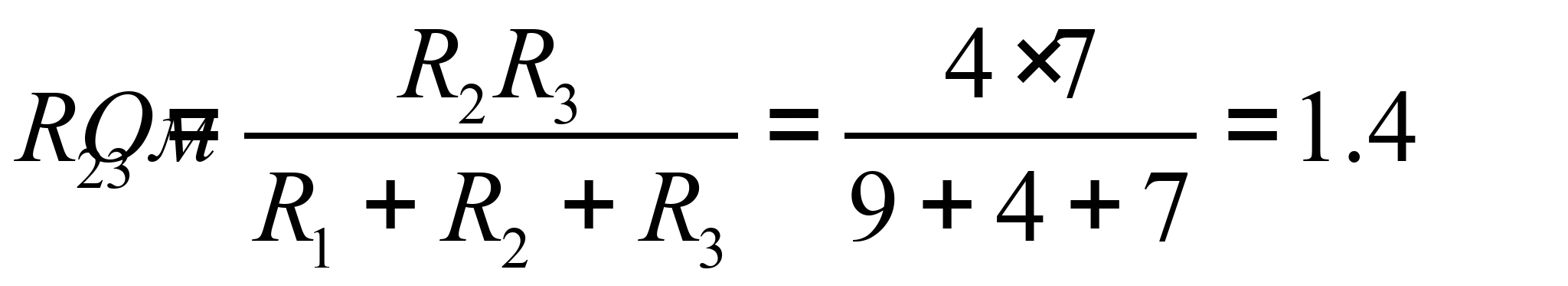
5. Расчет схемы, полученной в п. 4, методом узловых напряжений.
Потенциал точки 
положим равным нулю.
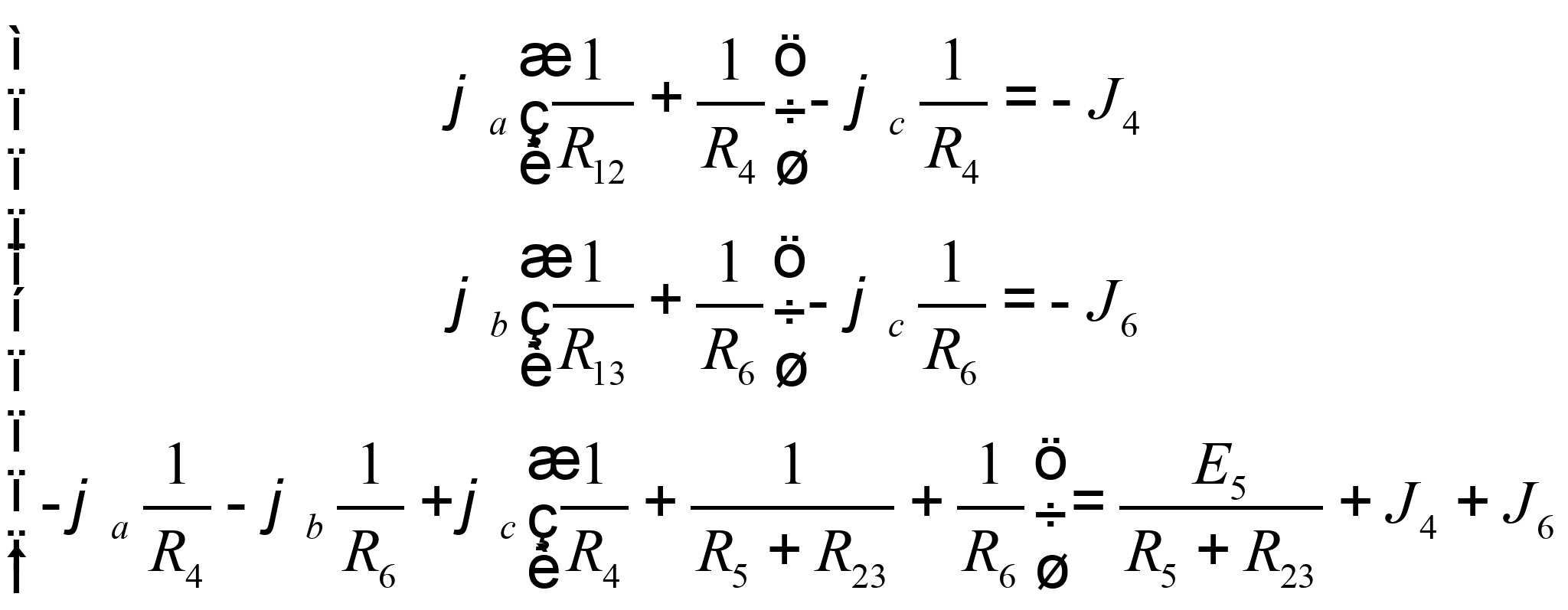
Подставляя числовые значения, получаем
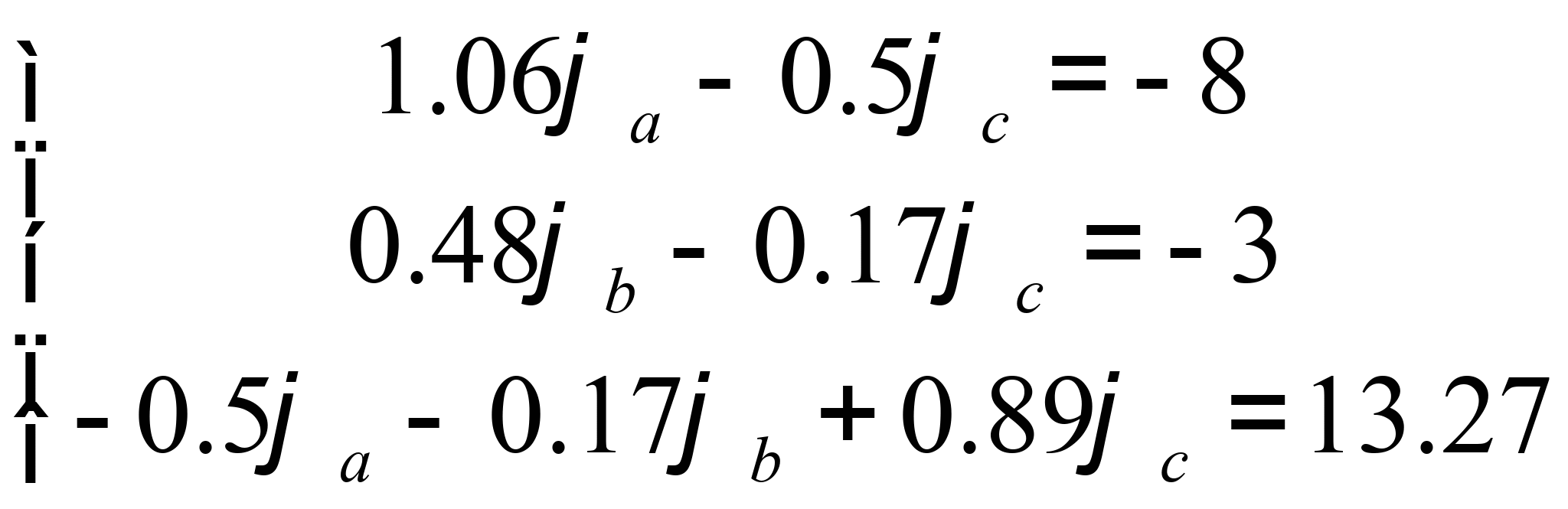
Решая систему, определяем потенциалы узлов
, 
, 
Определяем токи в ветвях схемы:
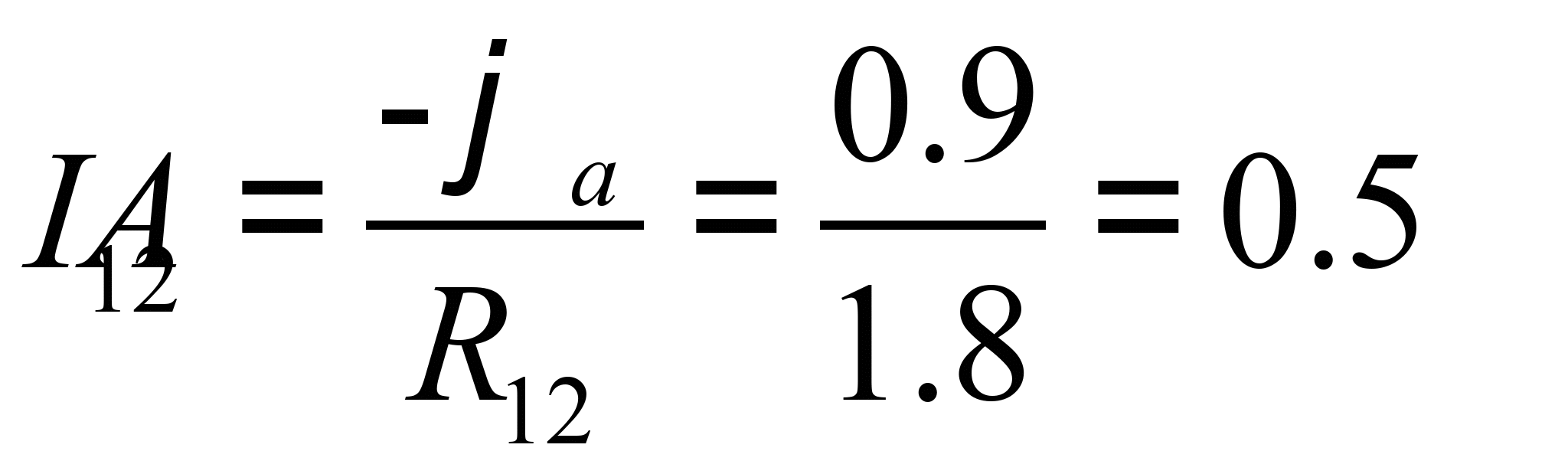
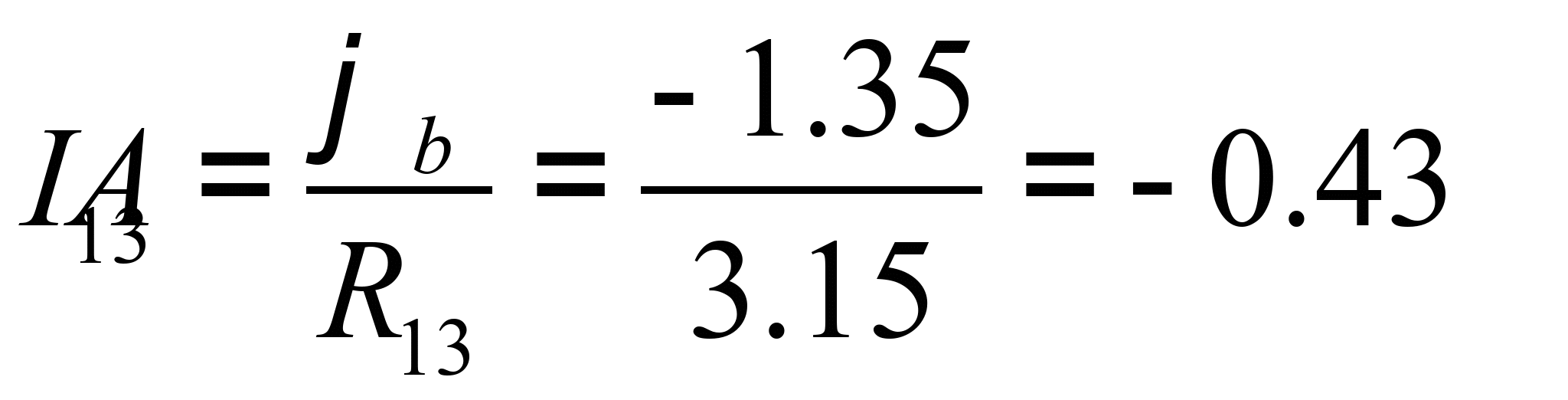
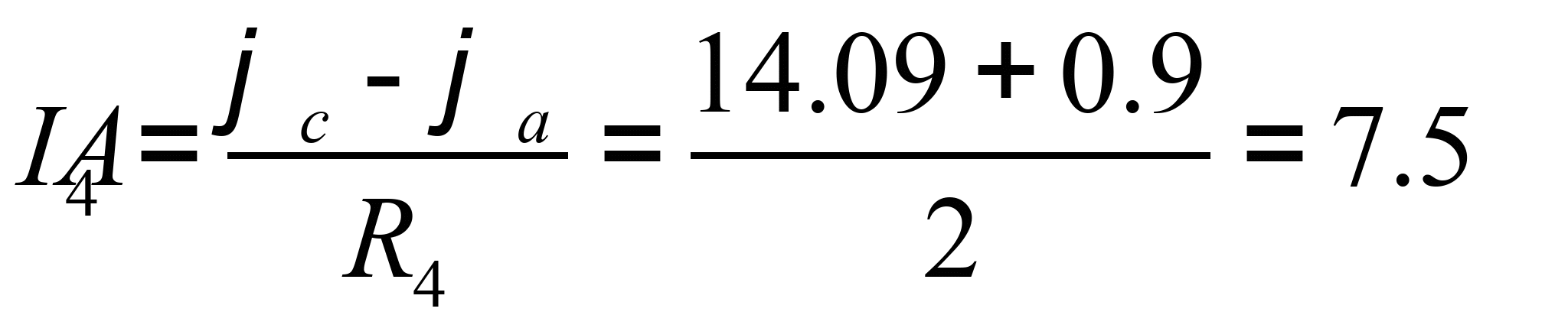
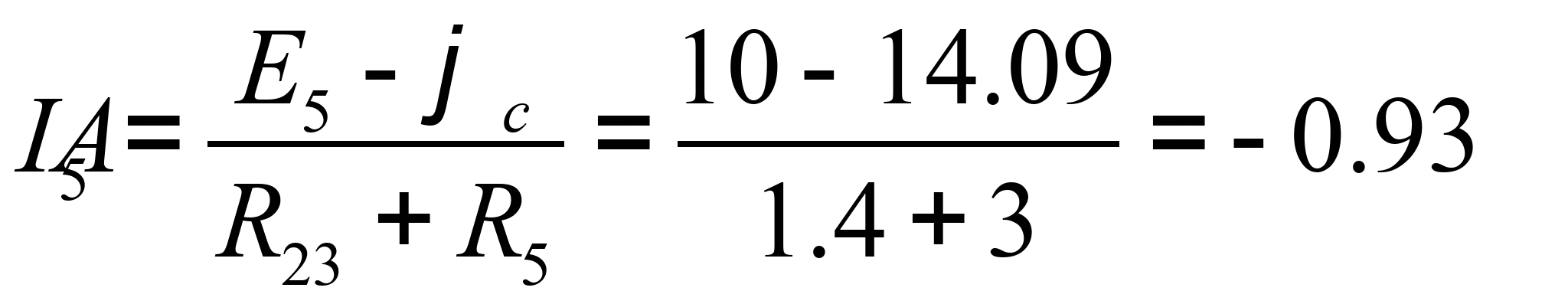
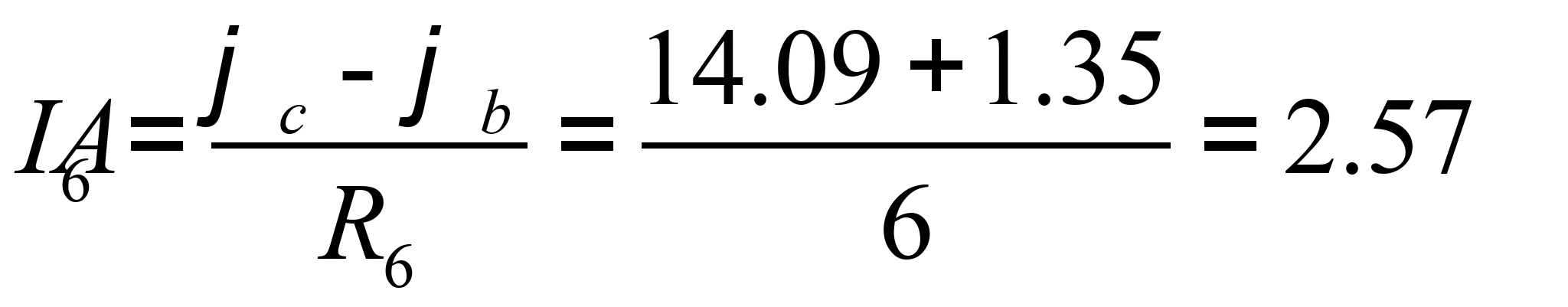
Результаты расчета совпадают с результатами, полученными в п. 3.
6. Определение тока в сопротивлении по методу эквивалентного генератора.
Для определения тока в сопротивлении методом эквивалентного генератора заменим расчетную цепь по отношению к зажимам резистора активным двухполюсником. В соответствии с теоремой Нортона активный двухполюсник может быть представлен параллельным соединением идеального источника тока, равного току короткого замыкания эквивалентного генератора, и резистора, равного внутреннему сопротивлению эквивалентного генератора.
Для определения тока короткого замыкания эквивалентного генератора воспользуемся уравнениями контурных токов, полученными в п. 3, в которых сопротивление резистора примем равным нулю.
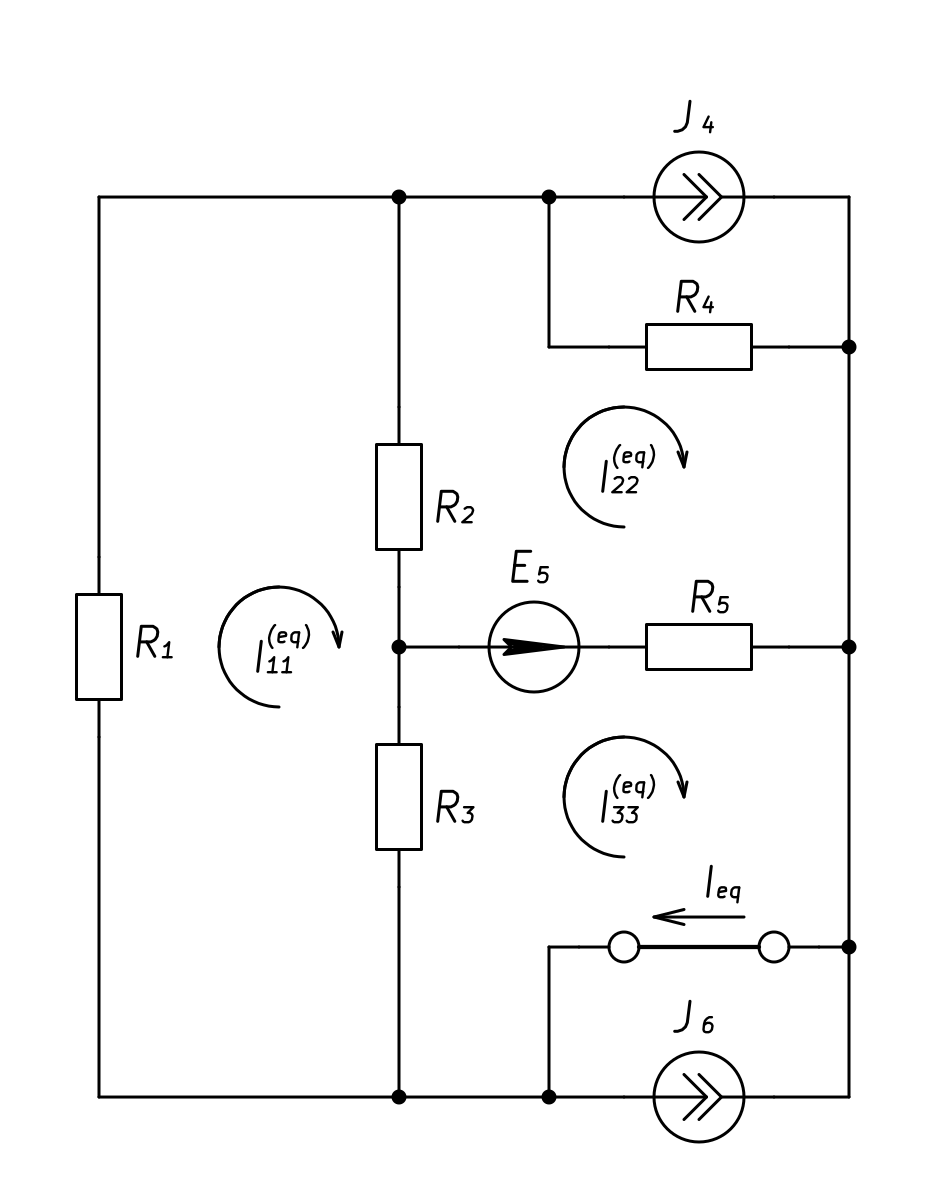
Рисунок 4. Схема расчетной электрической цепи для определения тока короткого замыкания эквивалентного генератора
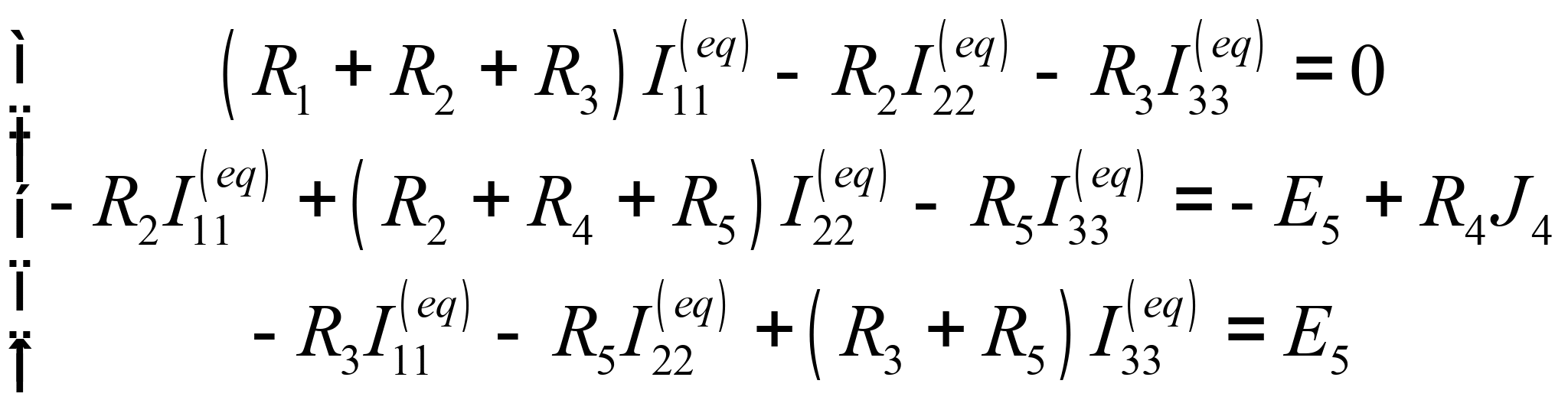
Подставляя числовые значения, получаем
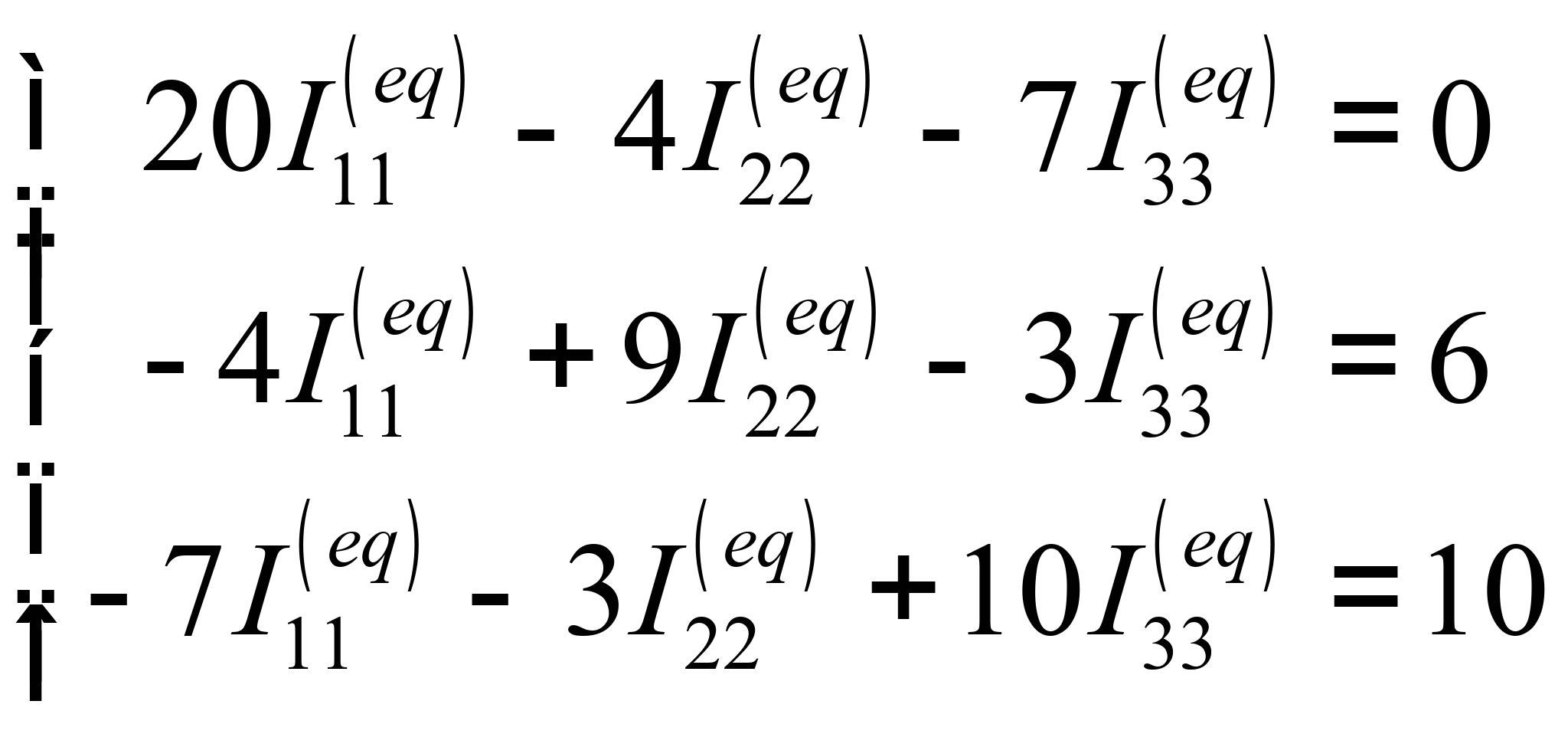
Решая систему, определяем контурные токи
, 
, 
Определяем ток короткого замыкания эквивалентного генератора:
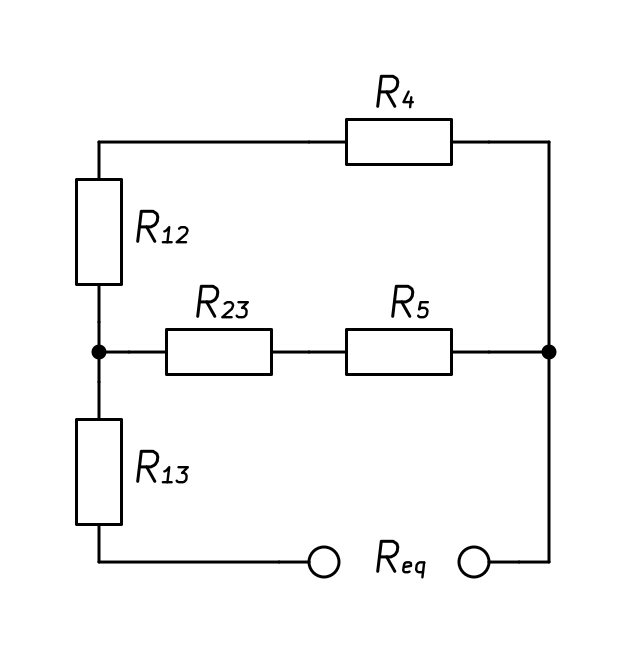
Рисунок 5. Схема расчетной электрической цепи для определения внутреннего сопротивления эквивалентного генератора
Внутреннее сопротивление эквивалентного генератора:
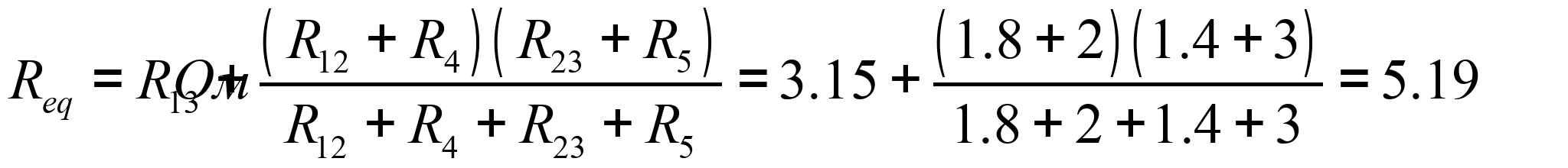
Схема для определения тока в сопротивлении методом эквивалентного генератора представлена на рисунке.
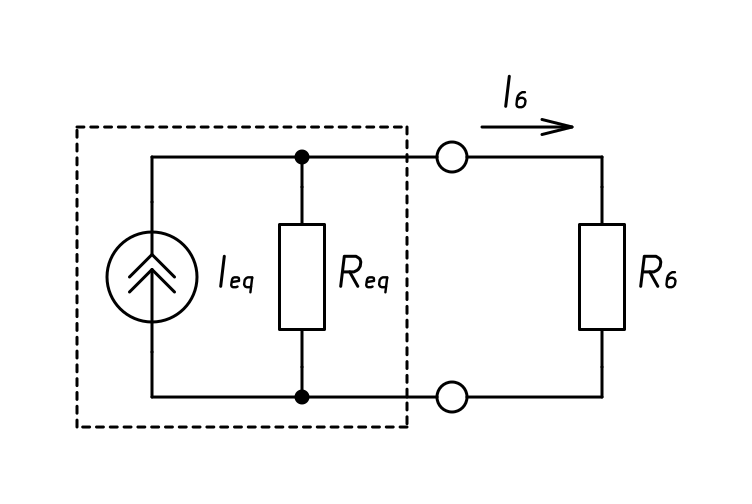
Рисунок 6. Схема определения тока в сопротивлении методом эквивалентного генератора
Ток в сопротивлении , определенный методом эквивалентного генератора равен:
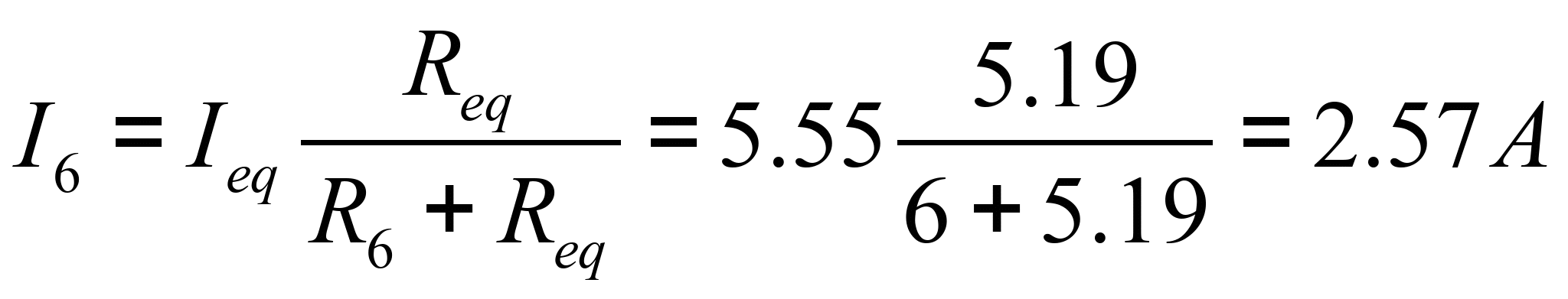
Полученное значение тока 
совпадает с результатом, полученным в п.п. 3, 5.
7. Расчет напряжения между точками и схемы.
Напряжение между точками и схемы равно
8. Составить баланс мощностей для исходной схемы.
Условием соблюдения баланса мощностей является равенство мощностей, отдаваемых источниками и потребляемых потребителями.
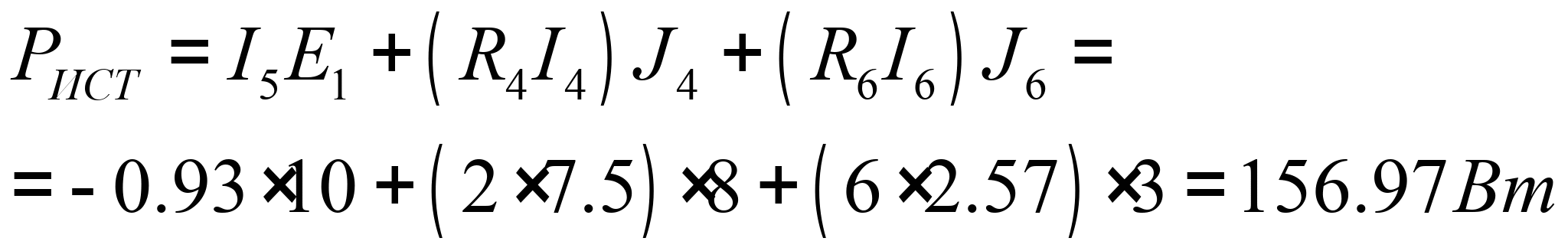
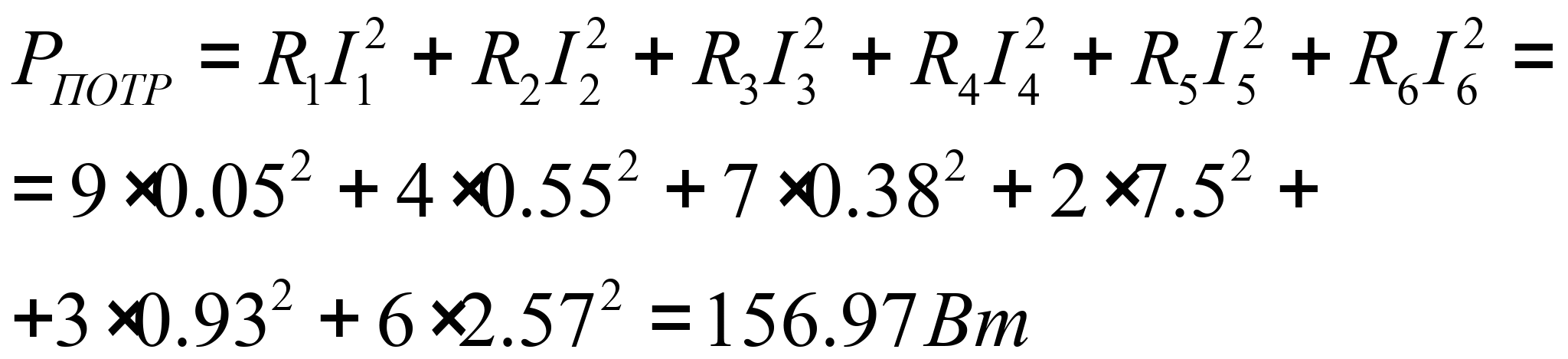
Из проведенного расчета видно, что баланс мощностей выполняется, значит расчет выполнен верно.
Оценка погрешности баланса мощностей
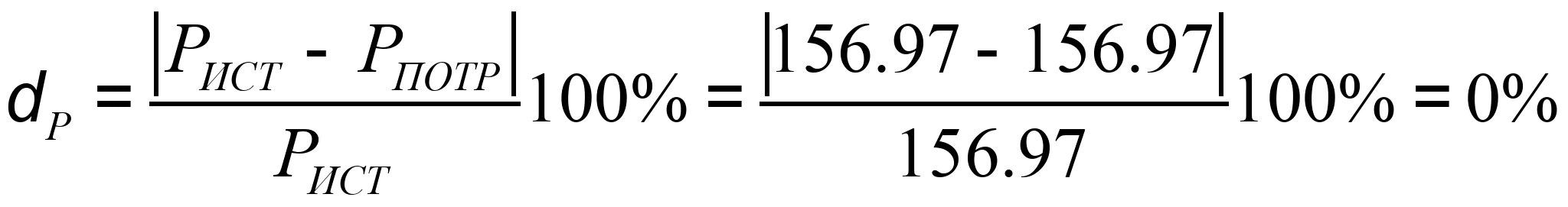
Задание 2. Расчет цепей по комплексным значениям.
Расчетная схема с выбранными для расчета направлениями токов ветвей и контурными токами приведена на рисунке.
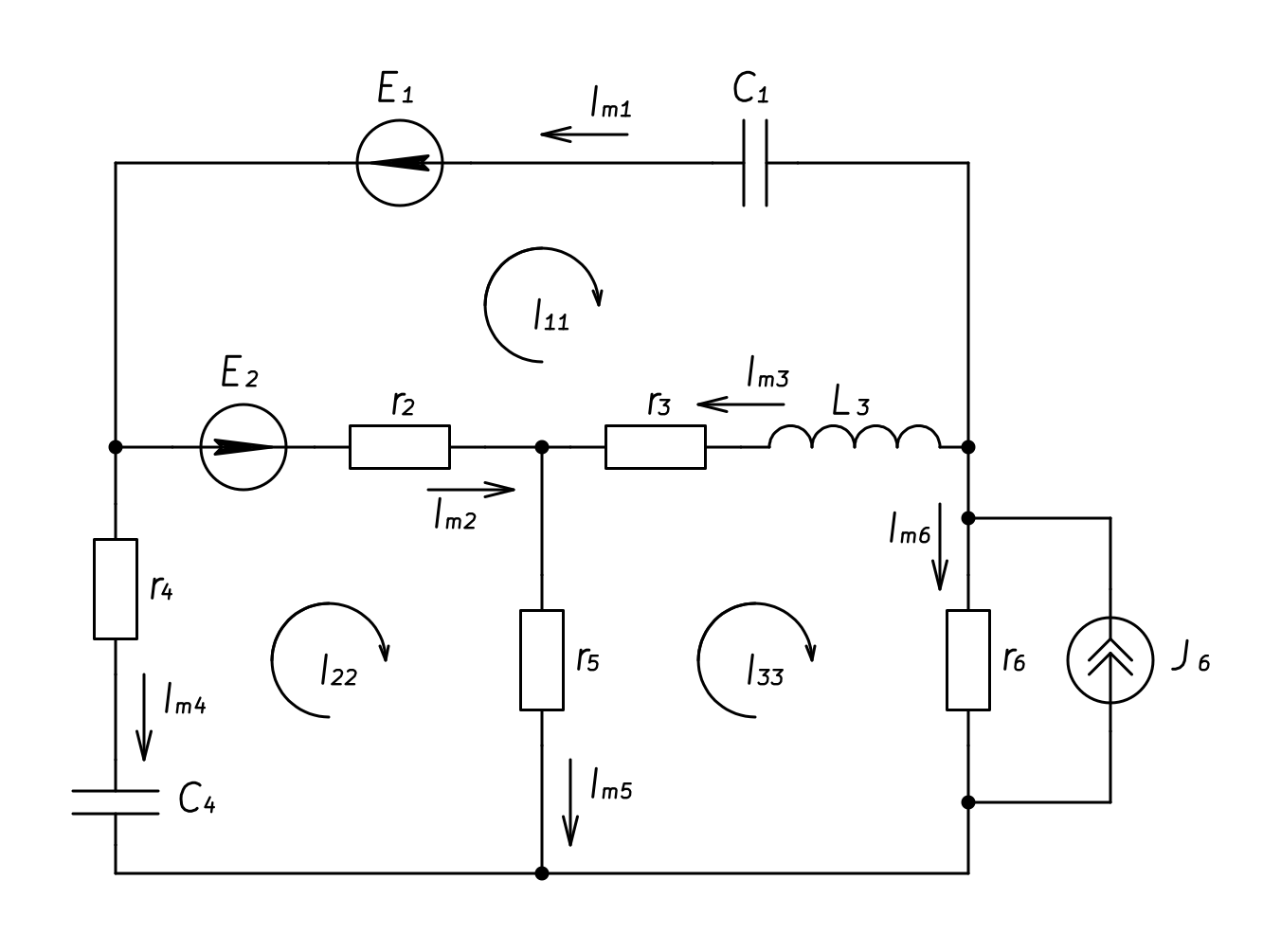
Рисунок 1. Схема расчетной цепи
Дано:
Применяя метод контурных токов для комплексных амплитуд выполнить следующее:
1. Определить амплитуды токов во всех ветвях схемы.
2. Определить напряжения на всех элементах внешнего контура.
3. Составить баланс активных и реактивных мощностей.
4. Построить векторную диаграмму токов цепи.
5. Построить векторную диаграмму для напряжений внешнего контура.
Решение.
Определим сопротивления пассивных элементов цепи.
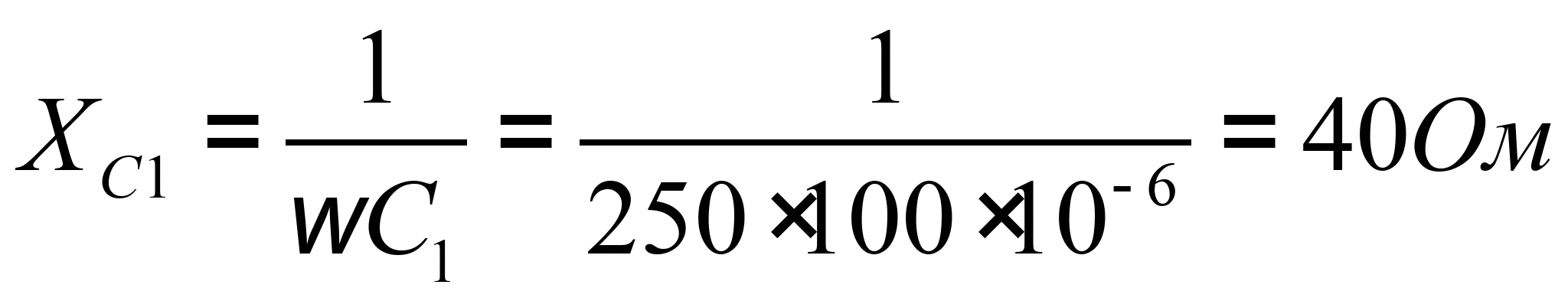
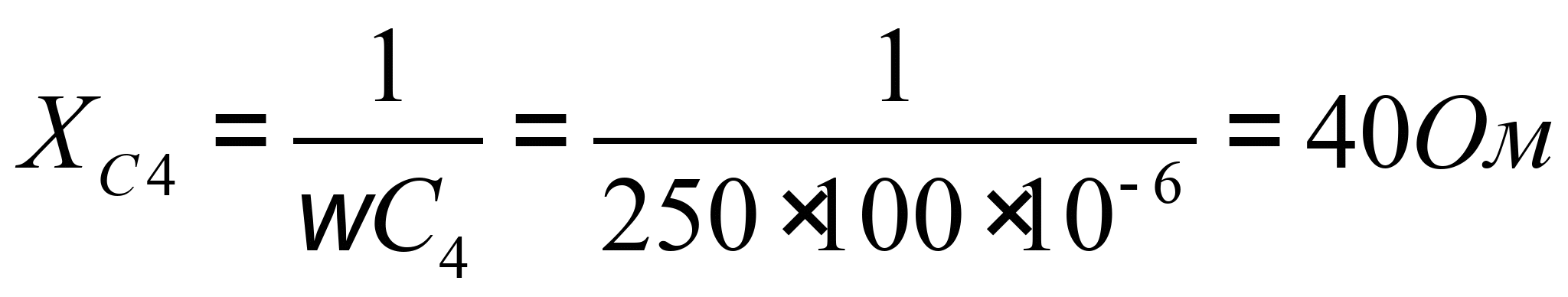
1. Определение амплитуд токов во всех ветвях схемы методом контурных токов.
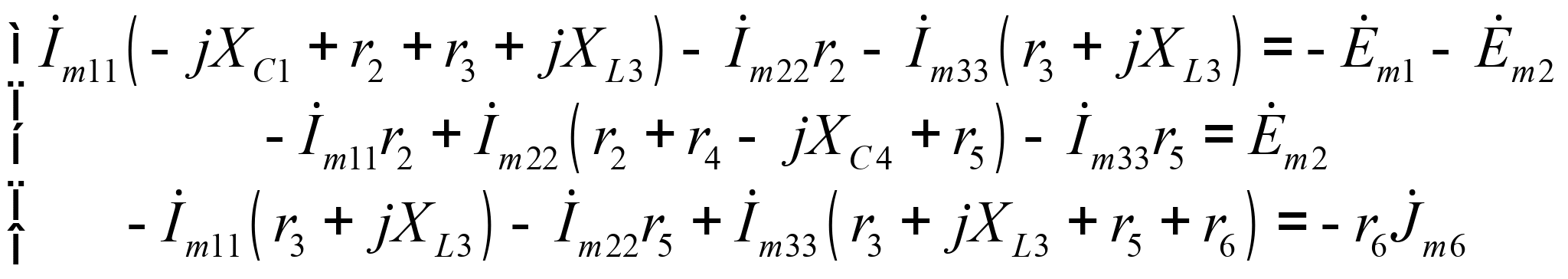
Подставляя числовые значения, получаем
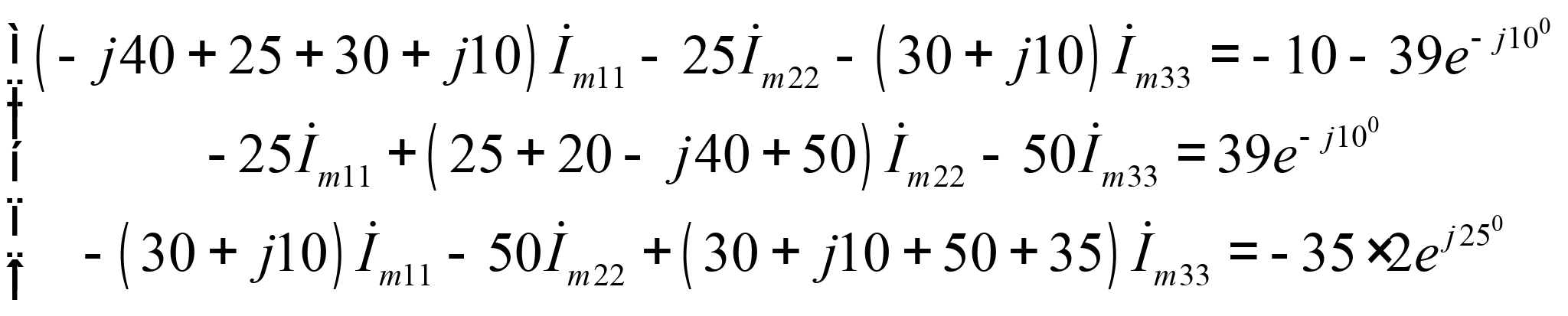
или
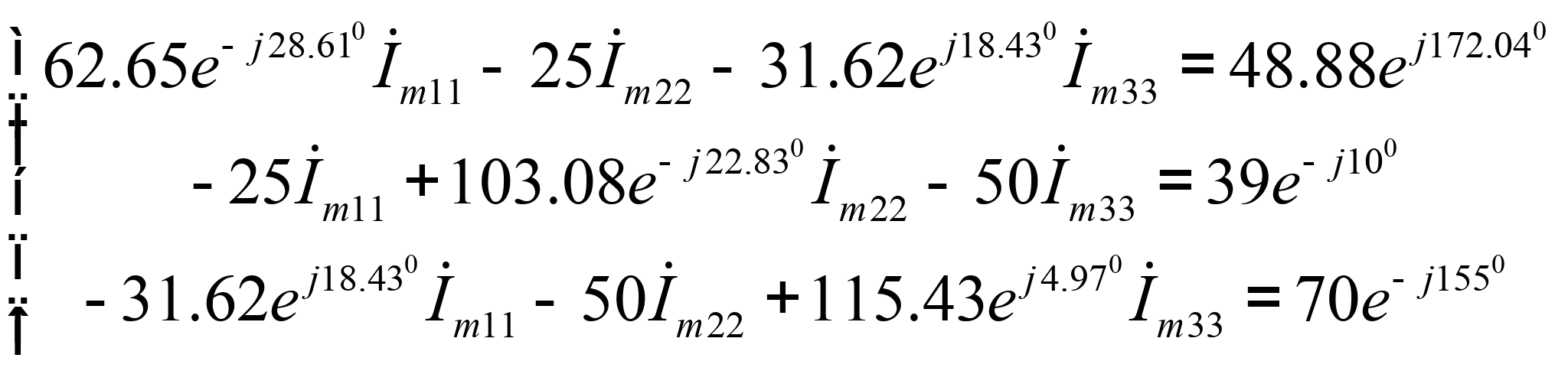
Решая систему, определяем комплексные амплитуды контурных токов
Определяем комплексные амплитуды токов в ветвях цепи
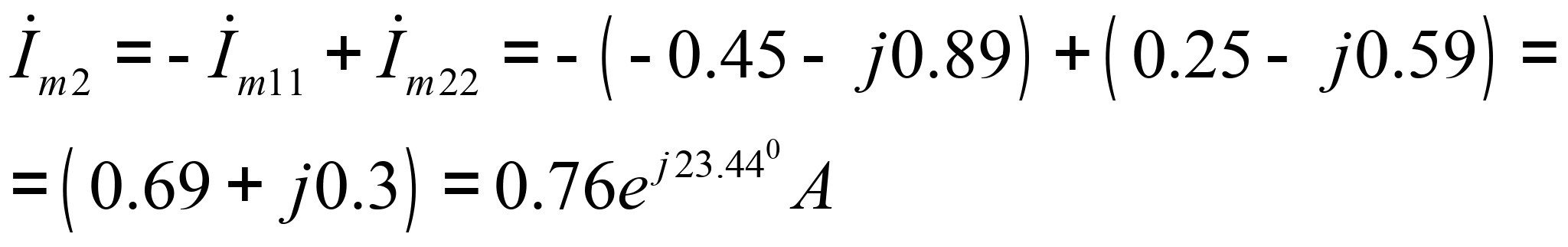
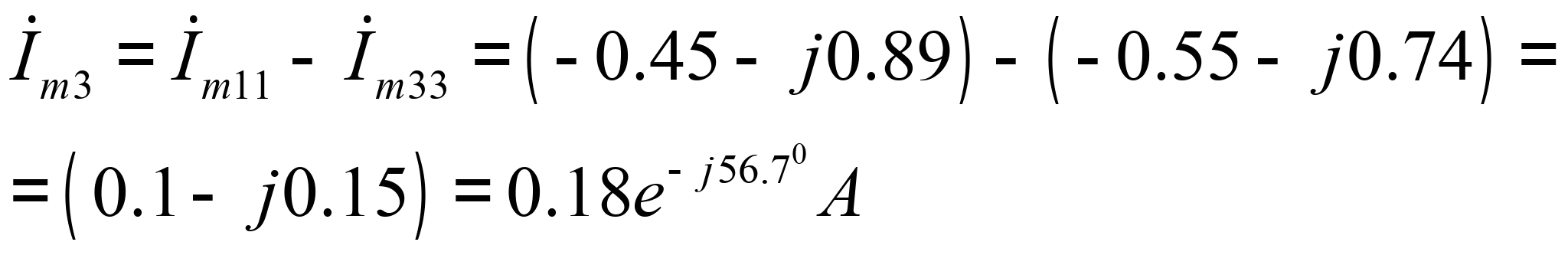
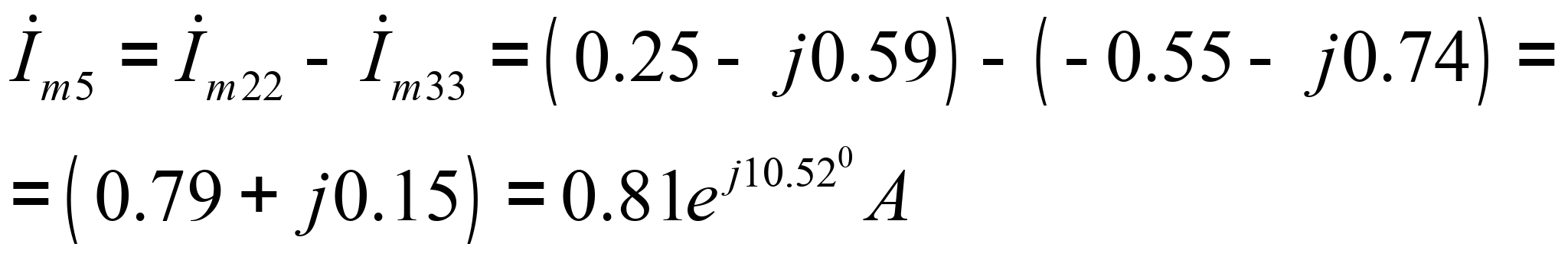
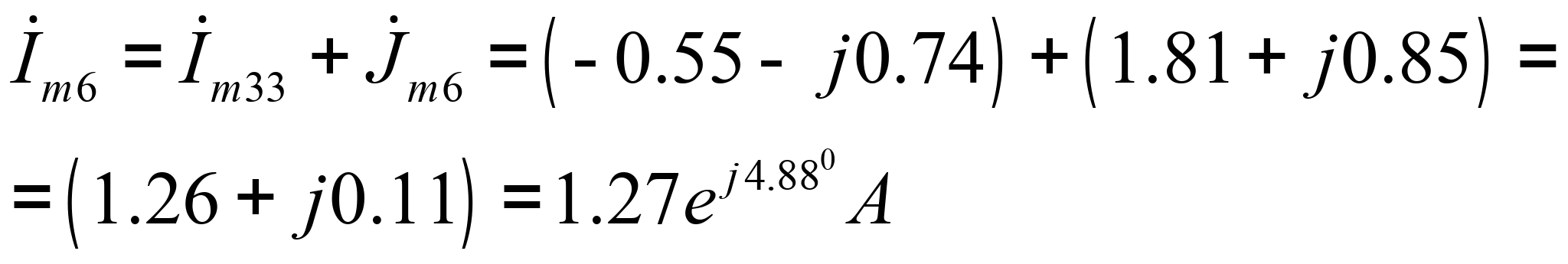
2. Определение напряжений на всех элементах внешнего контура.
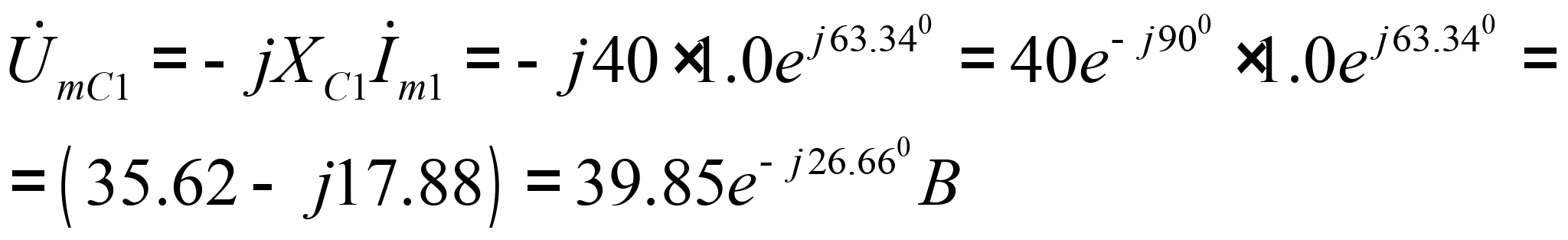
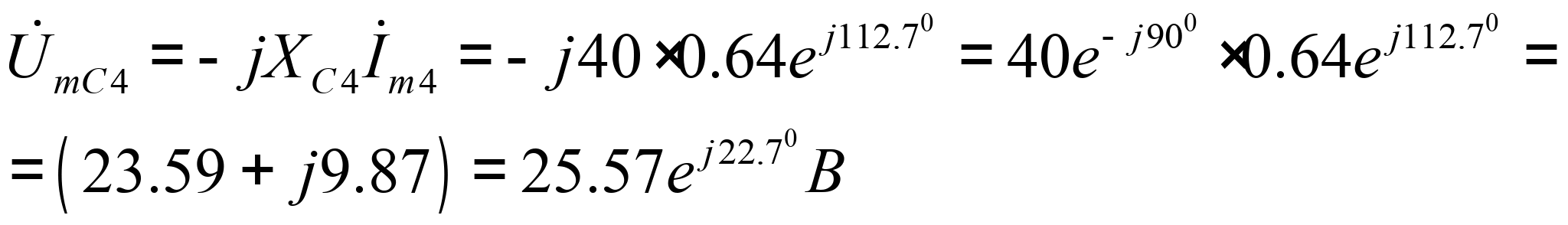
3. Составление баланса активных и реактивных мощностей.
Условием соблюдения баланса мощностей является равенство мощностей, отдаваемых источниками и потребляемых приемниками.
Мощность, отдаваемая источниками
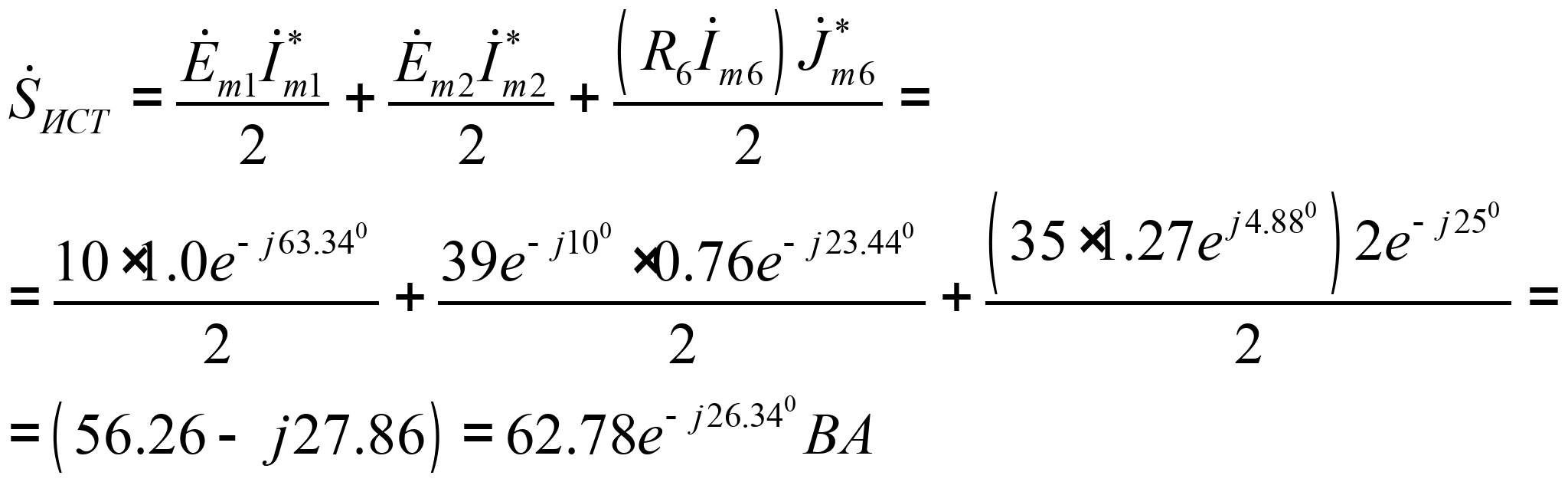
Мощность, потребляемая приемниками
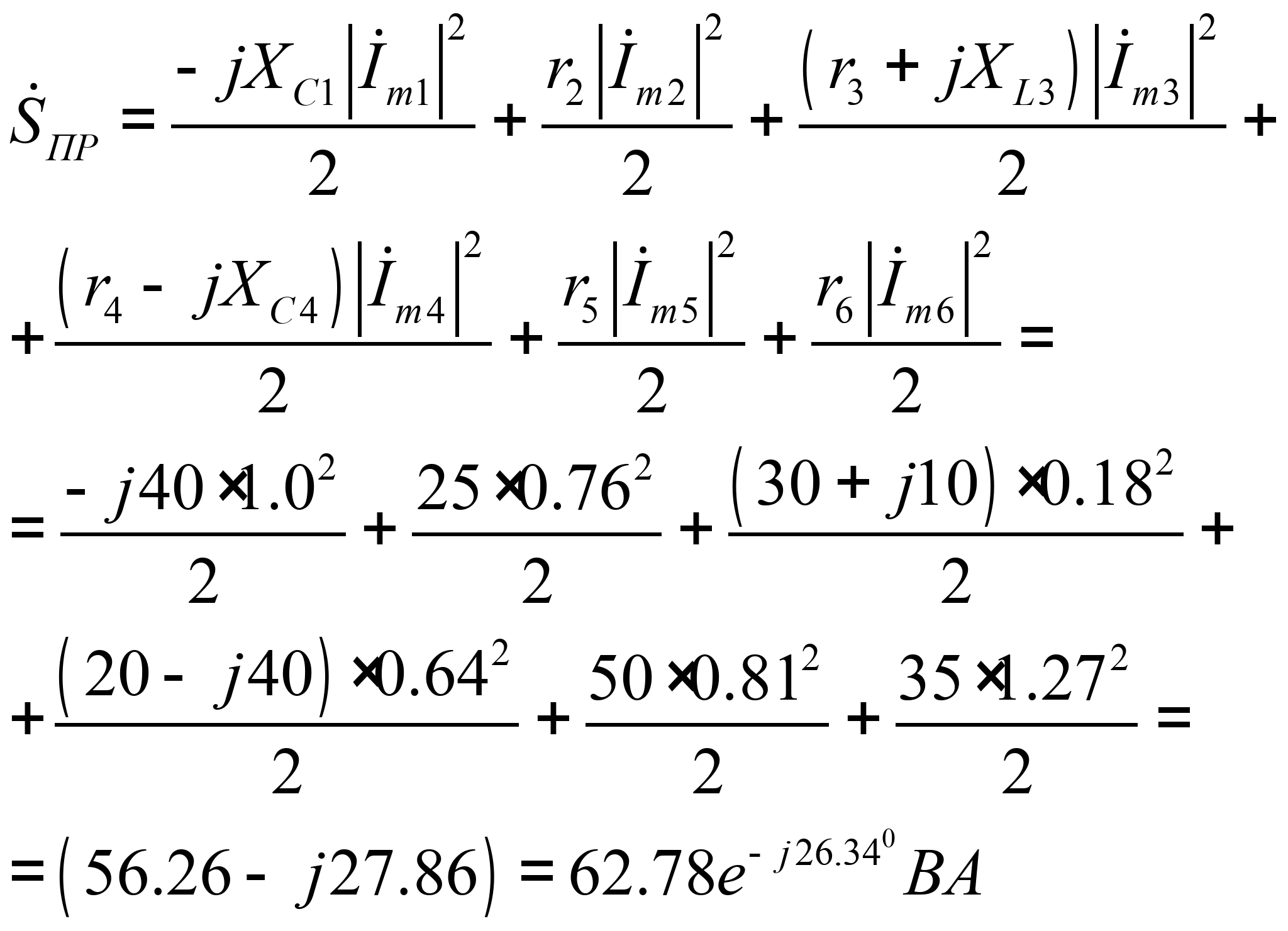
Из результатов расчетов видно, что
,
т.е. баланс мощностей соблюдается.
4. Построение векторной диаграммы токов цепи.
Векторная диаграмма токов цепи представлена на рисунке.
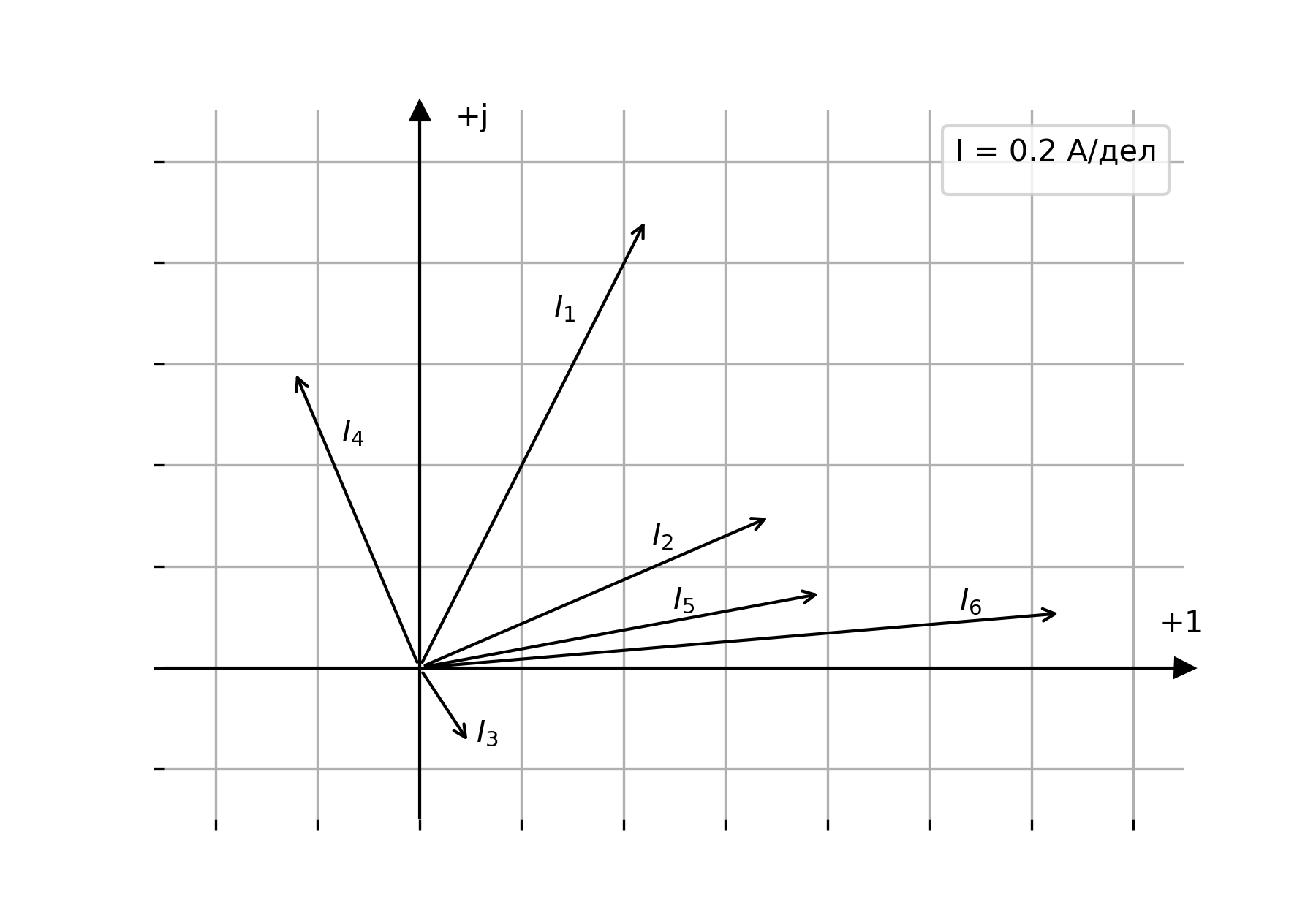Рисунок 2. Векторная диаграмма токов цепи.
5. Построение векторной диаграммы для напряжений внешнего контура.
Напряжения на элементах внешнего контура цепи рассчитаны в п. 2.
Векторная диаграмма для напряжений внешнего контура цепи представлена на рисунке.
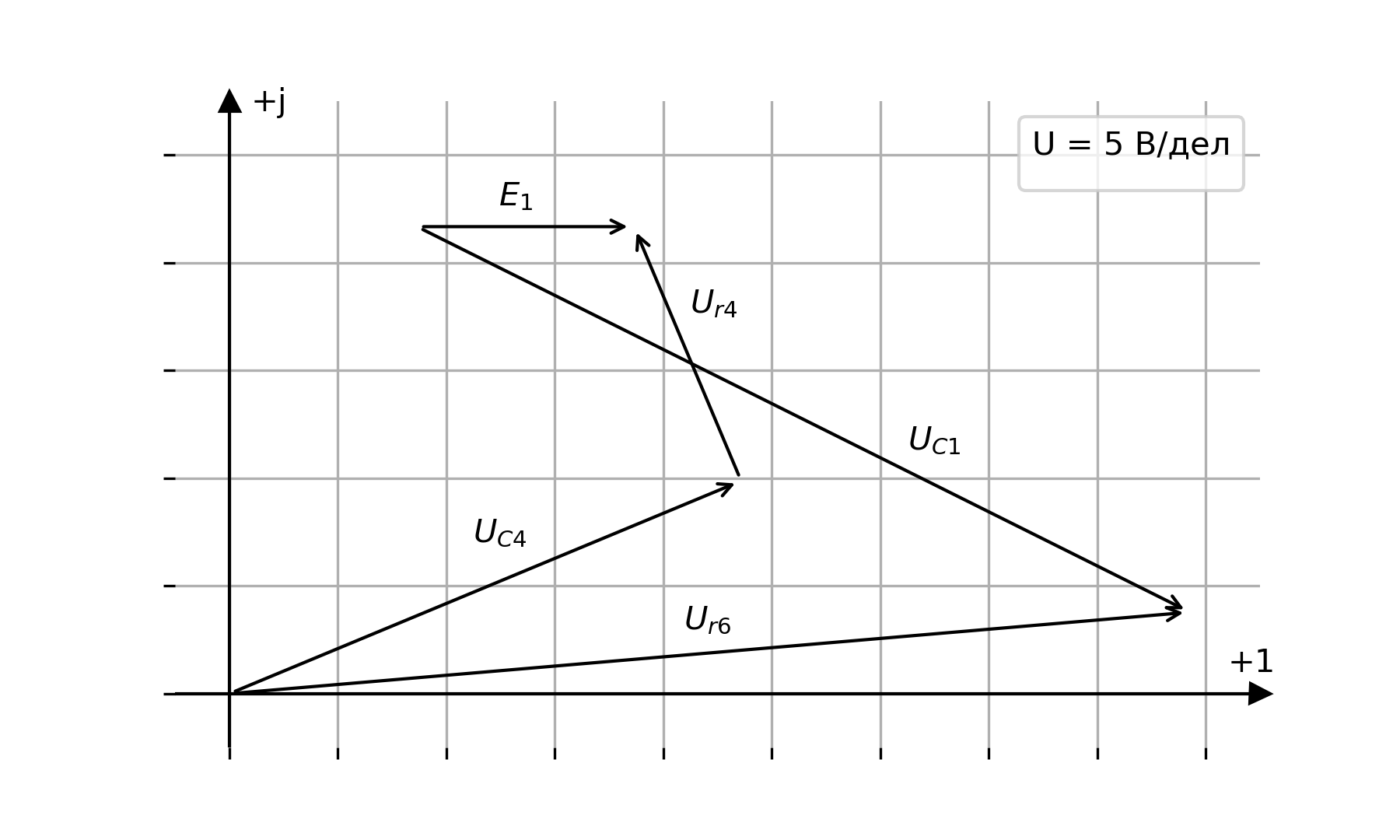
Рисунок 3. Векторная диаграмма для напряжений внешнего контура цепи.
Задание 3. Расчет резонансных схем.
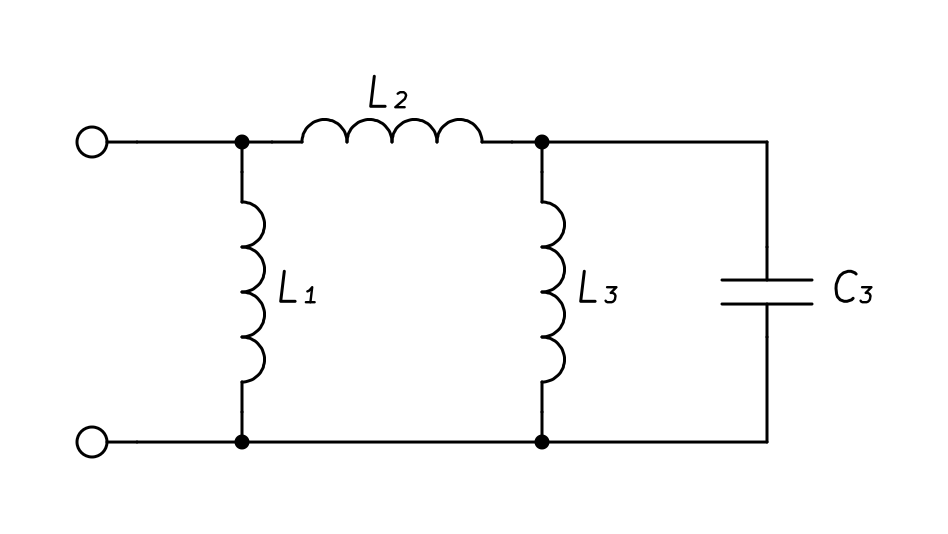
Рисунок 1. Схема расчетной цепи
Дано:
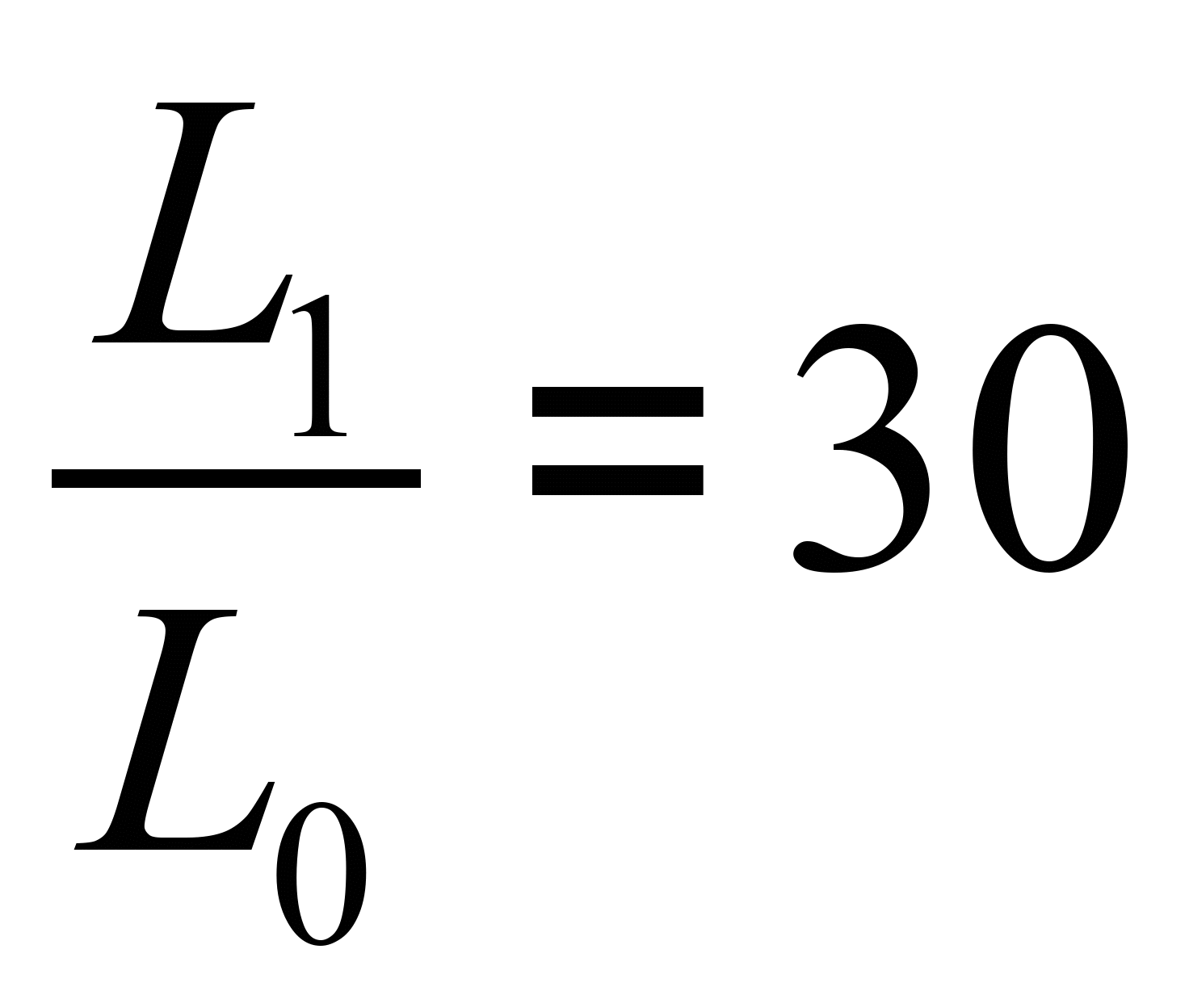
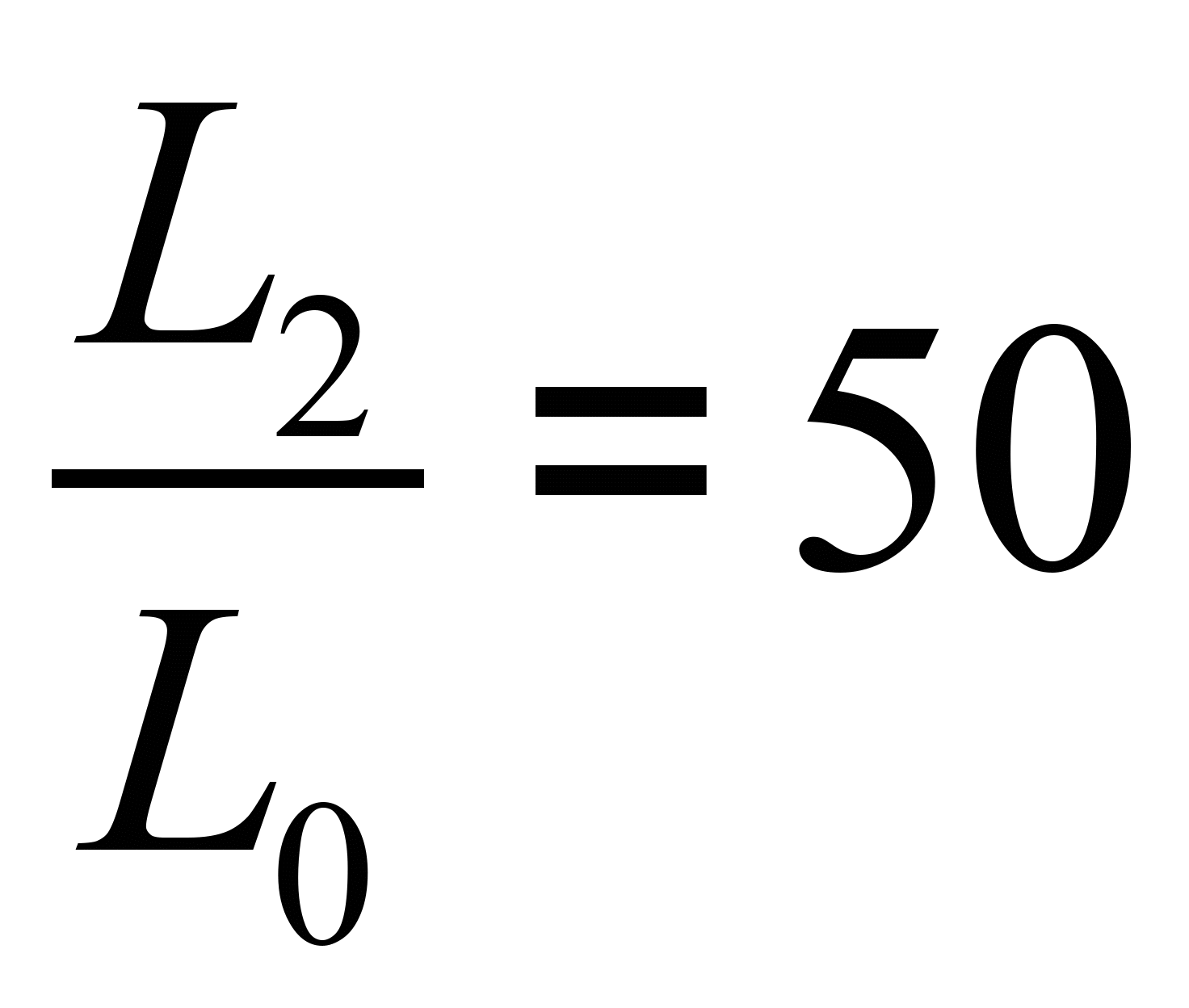
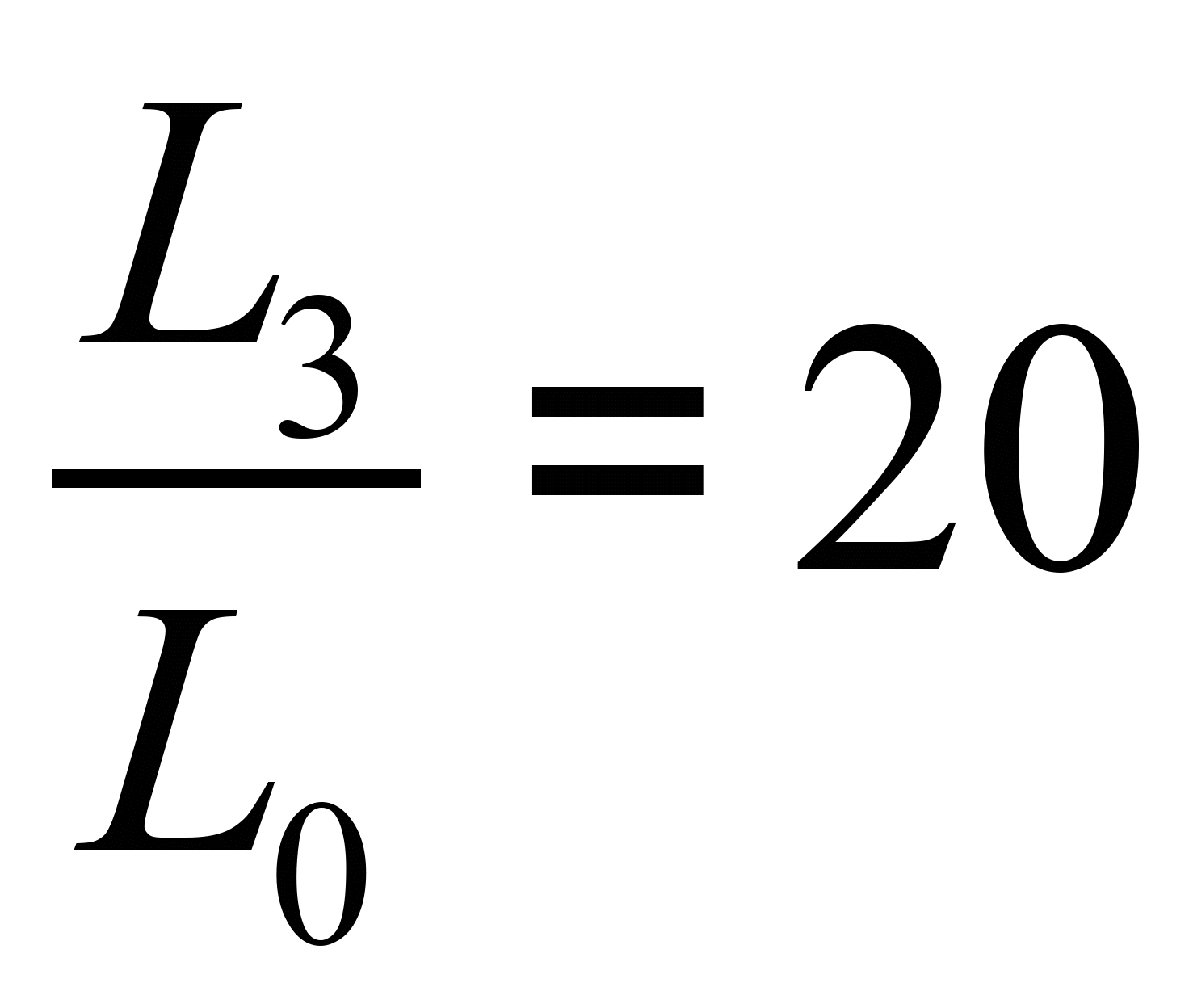
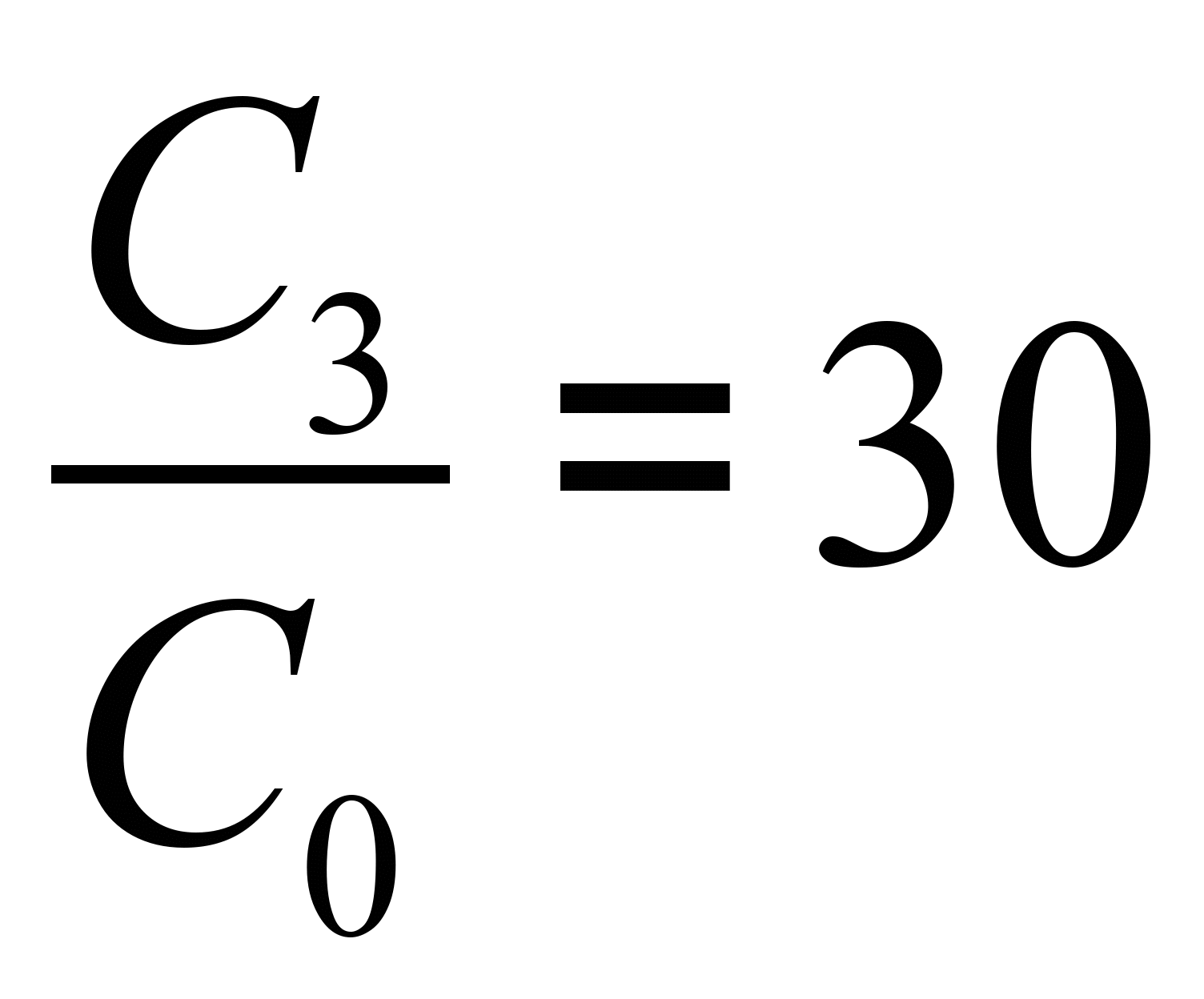
Требуется определить резонансные частоты и построить график частотной характеристики входного сопротивления (или входной проводимости).
Решение.
1. Определим значения реактивных элементов цепи.
2. Определим входное сопротивление цепи и приведем его к каноническому виду, т.е. представим в виде отношения двух полиномов по степеням 
.
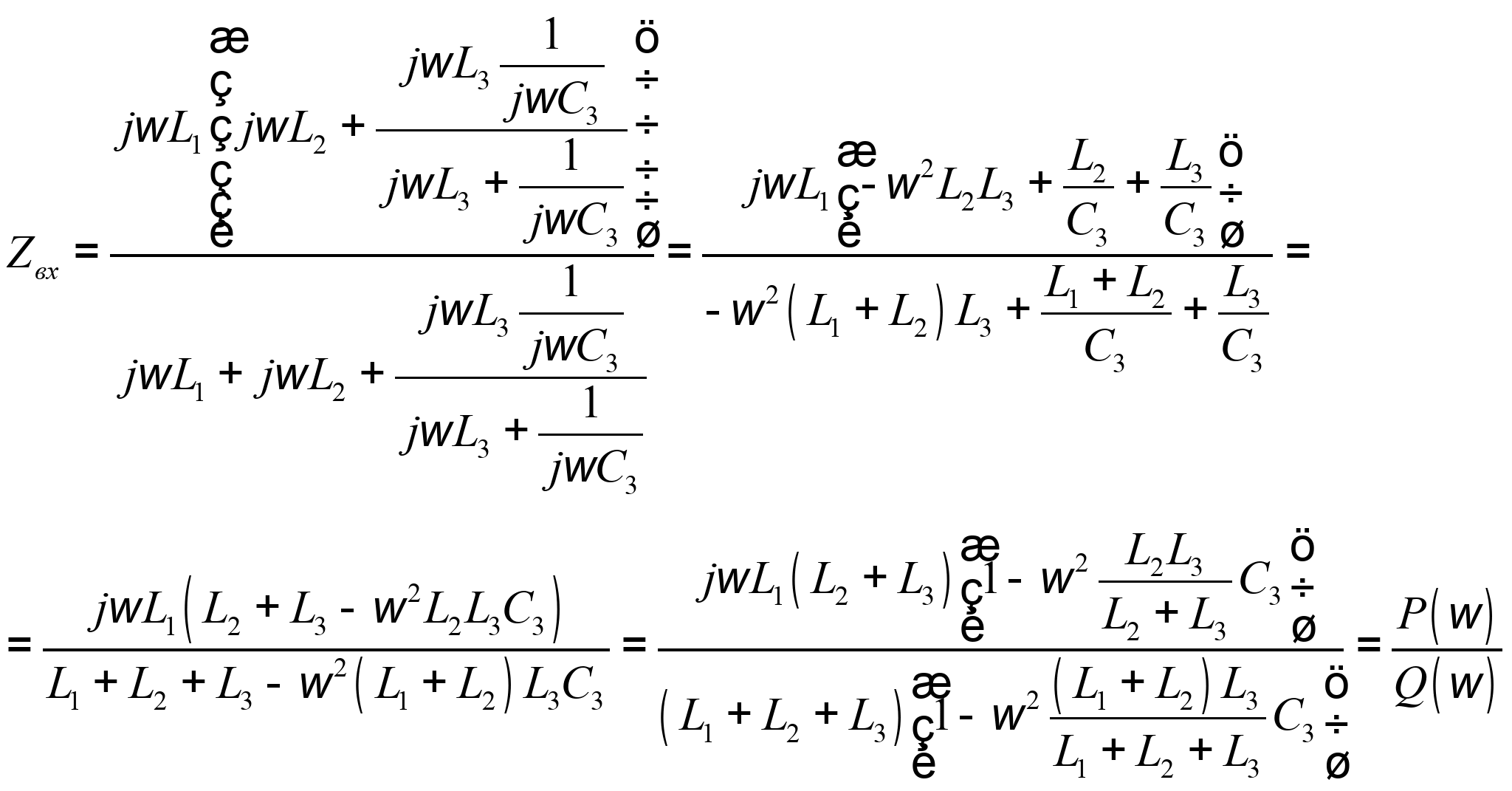
Тогда корни уравнения 
дадут частоты резонанса напряжения, а корни уравнения 
дадут частоты резонанса тока.
Из уравнения определим частоту резонанса напряжения:
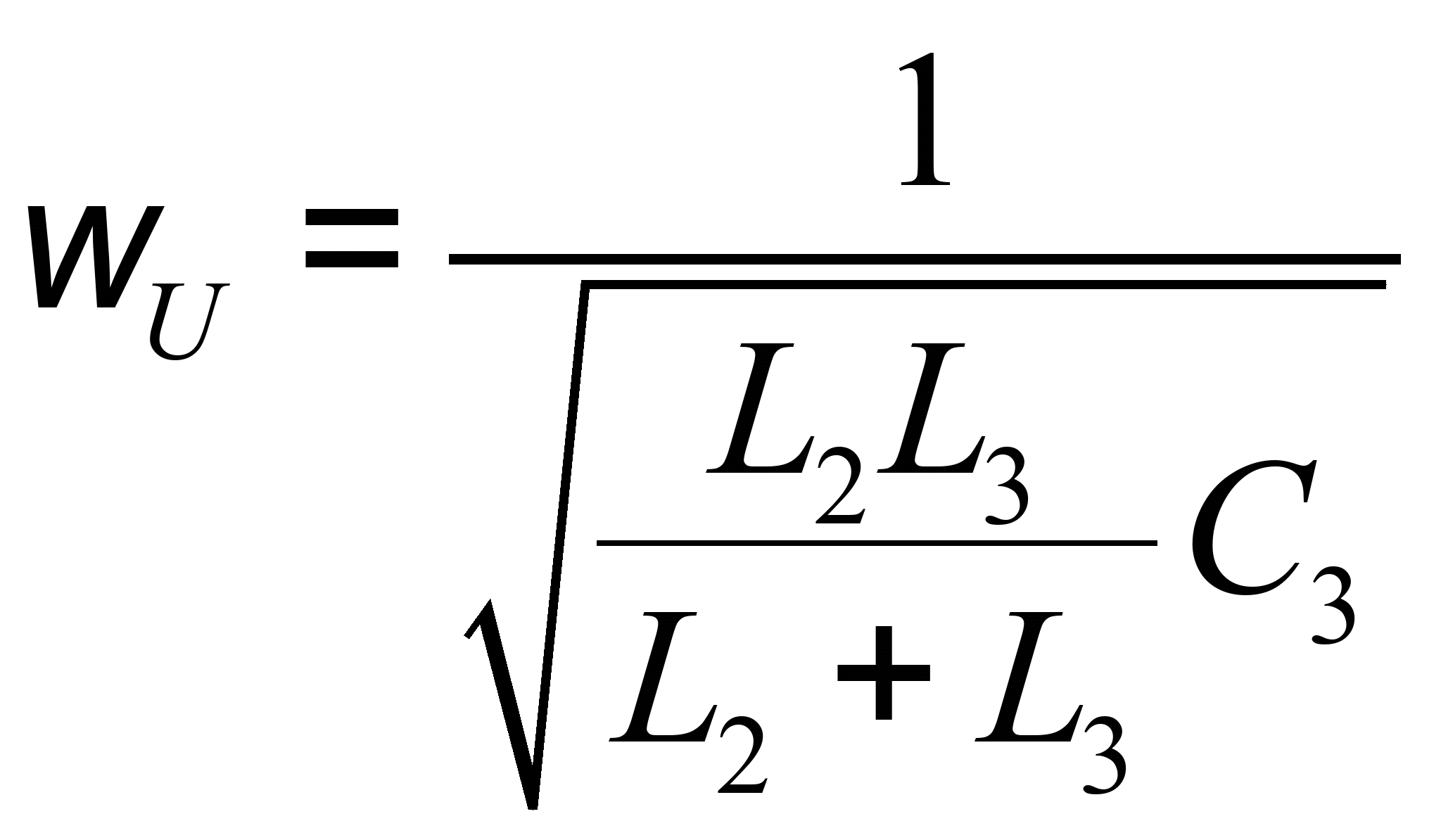
Из уравнения определим частоту резонанса тока:
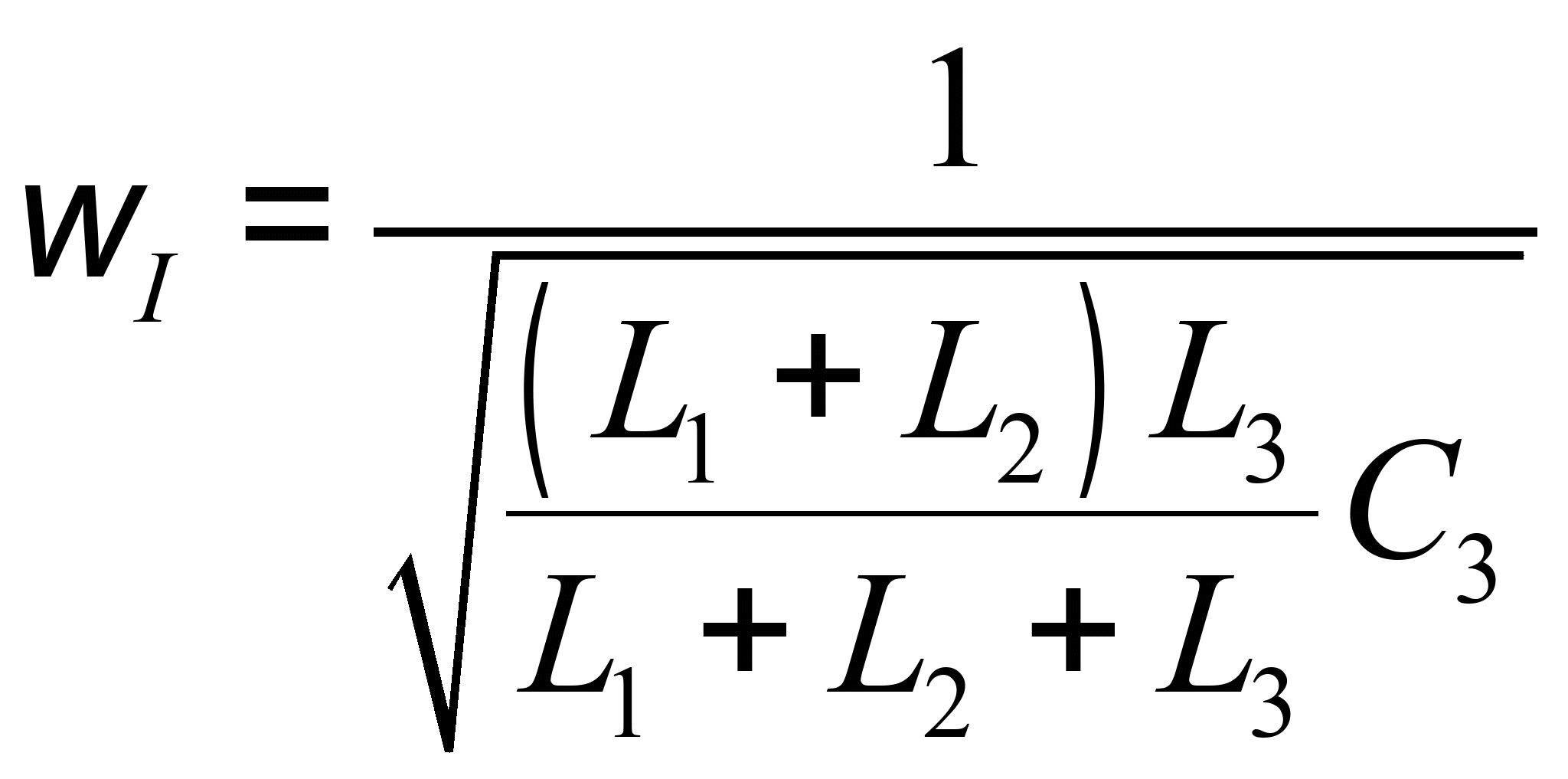
Подставляя числовые значения, получаем:
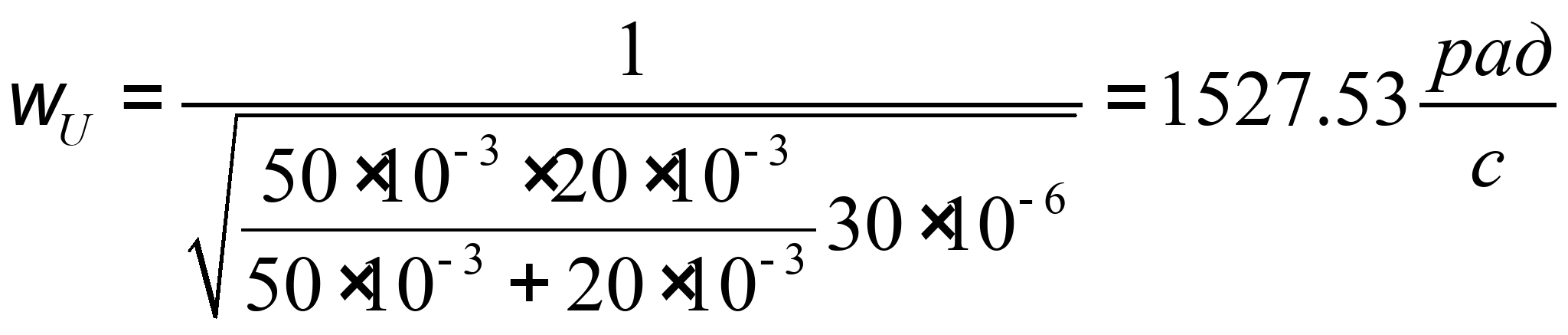
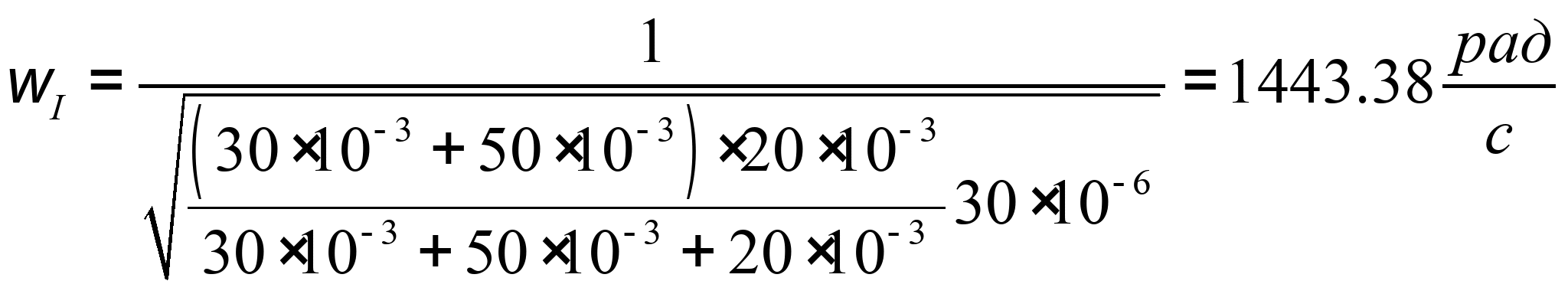
Или
График частотной характеристики входного сопротивления цепи представлен на рисунке.
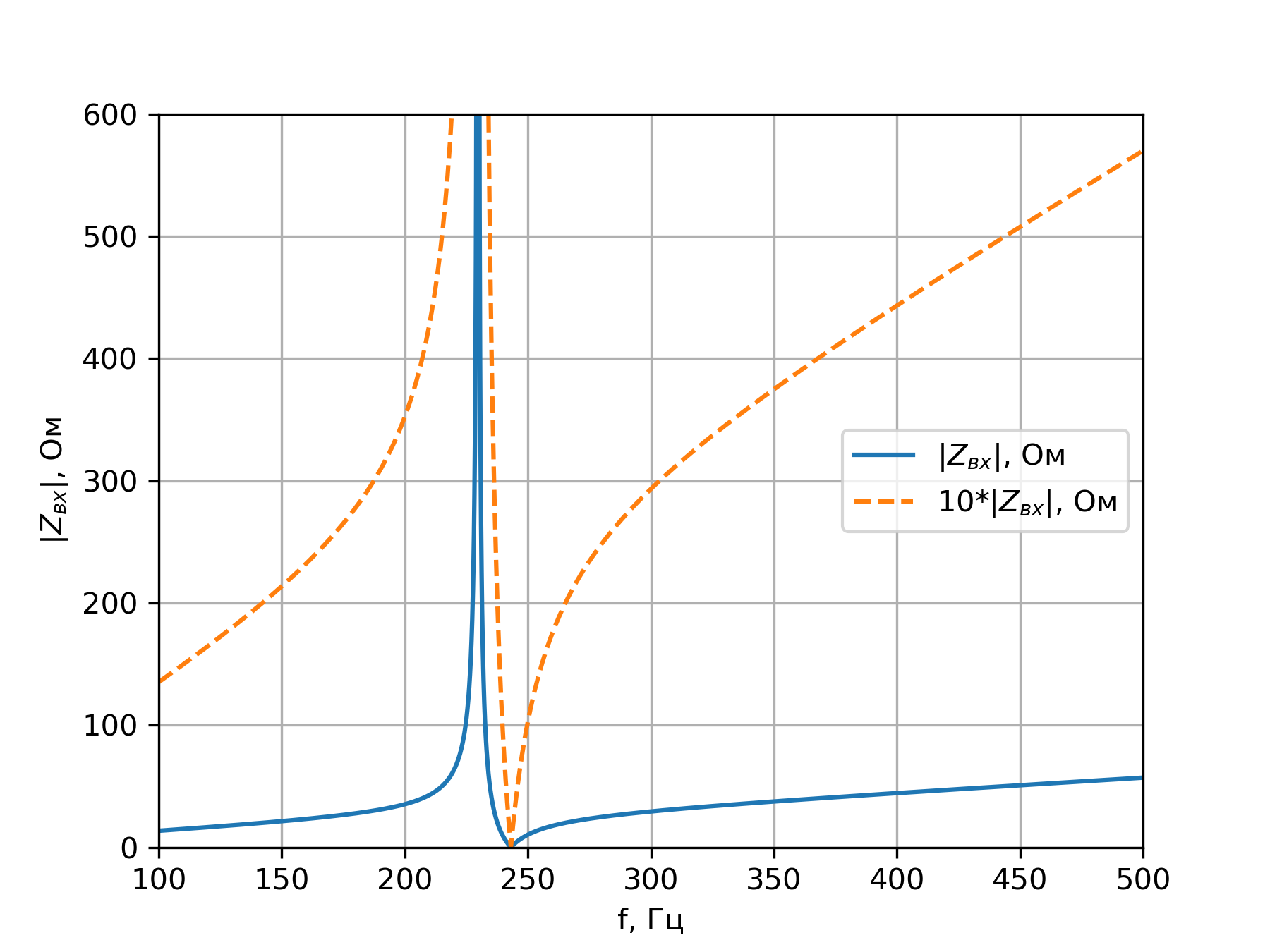
Рисунок 2. Частотная характеристики входного сопротивления цепи.
Для наглядности на графике штриховой линией представлено входное сопротивление в десятикратном увеличении.
Список литературы
1. Бессонов Л.А. Теоретические основы электротехники. Электрические цепи. – М.: Высш. шк., 2009. – 638 с.
2. Атабеков Г.И. Основы теории цепей. – СПб.: Лань, 2009. – 432 с.
3. Сборник задач по теоретическим основам электротехники / Под ред. Л.А. Бессонова. – М.: Высш. шк., 2003. – 528 с.