Пример решения контрольной по электротехнике - 2

  На рисунке, изображён магнитопровод с воздушным зазором. Материал сердечника - электротехническая сталь. Размеры сердечника по средней магнитной линии в мм : ℓ1=280 мм ; ℓ2=330 мм ; ℓ3=370 мм ; ℓ0=2 мм. Толщина сердечника 50 мм. В сердечнике требуется создать магнитный поток Ф=0,0048 Вб. Определить ток, который должен проходить по обмотке катушки, если она имеет w=800 витков. Вычислить, также ток катушки, для создания заданного магнитного потока, если в сердечнике будет отсутствовать воздушный зазор.

  Дано : ℓ1=280 мм ; ℓ2=330 мм ; ℓ3=370 мм ; ℓ0=2 мм ; d=50 мм ; w=800 ; Ф=0,0048 Вб.

  Найти : I

                                                                            Решение.

 

  1. Начертим схему замещения магнитной цепи.

Цепь содержит три участка : первый состоит из одного участка – электротехнической  стали ; второй из одного участка – электротехнической  стали ; третий из двух участков - электротехнической стали и воздушного зазора.

 

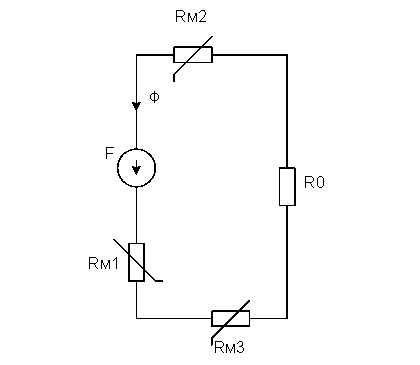
  Найдём длины и площади сечения участков.

Первый участок : S1=0.05×0.1=5×10-3 м2 ; ℓ1=280 мм=0,28 м

Второй участок : S2=0.05×0.08=4×10-3 м2 ; ℓ2=330 мм=0,33 м ;

Третий участок : S3=0.05×0.08=4×10-3 м2 ; ℓ3=370 мм=0,37 м.

2. Составим для магнитной цепи уравнения по законам Кирхгофа.

  По второму закону Кирхгофа составляем одно уравнение.

  Ф(Rм1+Rм2+Rм3+R0)=F       (1)

  Найдём магнитные индукции на каждом участке : B1=Ф/S1=0.0048/0.005=0.96 Тл ;

   B2=B3=B0=Ф/S2=Ф/S3=0.0048/0.004=1.2 Тл

  Найдём напряжённости магнитного поля на каждом участке : на участках из электротехнической стали напряжённость поля находим по кривой намагничивания

  H1=600 А/м ; H2=H3=1400 А/м.

Напряжённость магнитного поля находим по формуле : H0=B0/μ0=1.2/(4π×10-7)=9.6×105 А/м

(где μ0=4π×10-7 Гн/м – магнитная постоянная).

  Запишем уравнение (1) :

  F=Iw=H1ℓ1+H2ℓ2+H3ℓ3+H0ℓ0=600×0.28+1400×0.33+1400×0.37+9.6×105×0.002=3068 А

  Откуда находим ток, который должен проходить по обмотке : I=3068/800=3.8 А

  Найдём ток в обмотке катушки, необходимый для создания магнитного потока Ф=0,0048 Вб, если воздушный зазор отсутсвует.

  F=Iw=H1ℓ1+H2ℓ2+H3(ℓ3+ℓ0)=600×0.28+1400×(0.33+0.37+0.002)=1150.8

  Откуда ток катушки : I=1150.8/800=1.4 А

  Ответ : 1) I=3.8 A ; 2) I=1.4 A.

 

 

 

  Задача 7.

  К переменному напряжению U=150 В частотой f=50 Гц подключены последовательно соединённые резистор и конденсатор. По цепи проходит ток I=3 А, при этом на резисторе возникает падение напряжения Ua=90 В. Начертить схему цепи. Определить полное сопротивление цепи z, сопротивление резистора R, сопротивление XC и ёмкость С конденсатора, коэффициент мощности cosφ, напряжение UC на ёмкостном сопротивлении. Построить в масштабе mu=20 В/см векторную диаграмму напряжений, отложив горизонтально вектор тока.

  Дано : U=150 В ; f=50 Гц ; I=3 А ; Ua=90 В.

  Найти : z , R , XC , C , cosφ , UC.

                                                                    Решение.

  Находим полное сопротивление цепи : z=U/I=150/3=50 Ом.

  Сопротивление резистора : R=Ua/I=90/3=30 Ом.

  Находим сопротивление XC : XC==40 Ом.

  Находим ёмкость конденсатора : C=1/(2πfXC)=1/(2×50×3.14×40)=79.6×10-6 Ф=79,6 мкФ.

  Находим коэффициент мощности цепи : cosφ=R/z=30/50=0.6

  Находим напряжение на ёмкости : UC=IXC=3×40=120 В.

  Для построения векторной диаграммы, найдём длины векторов : ℓUa=Ua/mu=90/20=4.5 см ;

  ℓUc=UC/mu=120/20=6 см.

  Построение векторной диаграммы начинаем с построения вектора тока I, который откладываем горизонтально. Вектор напряжения Ua откладываем параллельно вектору тока I. От конца вектора Ua откладываем вектор напряжения UC перпендикулярно вектору тока I, в сторону его опережения. Геометрическая сумма векторов Ua и UC даёт вектор U.

  Схема цепи и векторная диаграмма построены на рисунке.

 

 

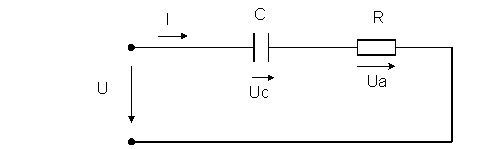
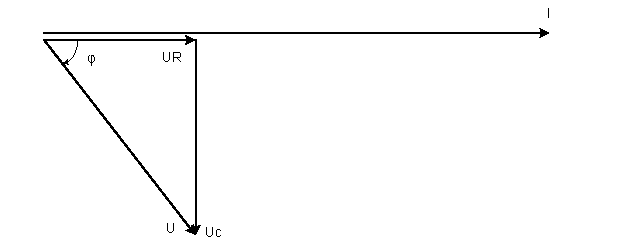
  Ответ : z=50 Ом ; R=30 Ом ; XC=40 Ом ; C=79,6 мкФ ; cosφ=0.6 ; UC=120 В.

 

 

 

 

 

  Задача 13.

  Последовательно с катушкой, активное сопротивление которой R=5 Ом и индуктивное XL=

  =26 Ом, включен конденсатор, ёмкостное сопротивление которого XC=14 Ом. Ток в цепи I=12 А, частота f=50 Гц. Начертить схему цепи. Определить полное сопротивление цепи z ; коэффициент мощности cosφ и напряжение на зажимах цепи U. Вычислить индуктивность катушки L0, при которой в цепи наступает резонанс напряжений. Для режима резонанса напряжений определить полное сопротивление цепи z0 ; ток I0 ; падение напряжения на активном Ua0 и ёмкостном UC0 сопротивлениях ; коэффициент мощности цепи cosφ0 ; полную S, активную P и реактивную Q мощности цепи. Построить в масштабе mu=50 В/см векторную диаграмму напряжений для режима резонанса, отложив горизонтально вектор тока.

  Дано : R=5 Ом ; XL=260 Ом ; XC=14 Ом ; I=12 A ; f=50 Гц.

  Найти : z ; cosφ ; U ; L0 ; z0 ; I0 ; Ua0 ; UC0 ; cosφ0 ; S ; P ; Q.

                                                                           Решение.

  Схема цепи приведена на рисунке.

 

  Полное сопротивление цепи : z==13 Ом

  Коэффициент мощности цепи : cosφ=R/z=5/13=0,38

  Напряжение, приложенное к цепи : U=Iz=12×13=156 В

  Найдём индуктивность катушки, которую нужно включить в сеть с конденсатором, чтобы в цепи возник резонанс напряжений. Условие резонанса :

  XL0=XC=14 Ом

  Индуктивность катушки : L0=XL0/(2πf)=14/(2×3.14×50)=0.045 Гн=45 мГн.

  Полное сопротивление цепи в режиме резонанса напряжений равно активному сопротивлению : z0=R=5 Ом.

  Ток в цепи в режиме резонанса напряжений : I0=U/z0=156/5=31,2 А.

  Падение напряжения на активном сопротивлении в режиме резонанса напряжений : Ua0=I0R=31.2×5=156 В.

  Падение напряжения на ёмкостном сопротивлении в режиме резонанса напряжений :

   UC0=I0XC=31.2×14=436.8 В.

  Коэффициент мощности цепи в режиме резонанса напряжений : cosφ0=R/z0=5/5=1

  Активная P, реактивная Q и полная S мощности цепи в резонансе напряжений :

  P=I02R=31.22×5=4867.2 Вт ; Q=0 ; S=P=4867.2 В∙А.

  Для построения векторной диаграммы найдём длины векторов : ℓUa=156/50=3.1 см ;

  ℓUc0=436.8/50=8.7 см.

  Построение векторной диаграммы начинаем с построения вектора тока I, который откладываем горизонтально. Вектор напряжения Ua0 откладываем параллельно вектору тока I. От конца вектора Ua0 откладываем вектор напряжение UC0 перпендикулярно вектору тока I в сторону отставания от него. От конца вектора UC0 откладываем вектор напряжения UL0 перпендикулярно вектору тока I в сторону его опережения (по модулю вектора UC0 и UL0 равны).

  Геометрическая сумма векторов Ua0 , UC0 и UL0 даёт вектор напряжения U, приложенного к цепи (U=Ua0).  

 

  Ответ : z=13 Ом ; cosφ=0.38 ; U=156 В ; L0=45 мГн ; z0=5 Ом ; I0=31.2 A ; Ua0=156 В ; UC0=

                =436.8 В ; cosφ0=1 ; P=4867.2 Вт ; Q=0 ; S=4867.2 В∙А.

 

 

 

 

 

 

   № 19

  Цепь переменного тока состоит из двух параллельных ветвей. В первую ветвь включены последовательно активное и индуктивное сопротивления : R1=12 Ом ; XL=9 Ом. Вторая ветвь состоит из последовательно соединённых активного и ёмкостного сопротивлений : R2=12 Ом ; XC=16 Ом. Напряжение на зажимах цепи U=220 В. Начертить схему цепи. Определить токи I1 , I2 в параллельных ветвях и ток I в неразветвленной части цепи ; коэффициент мощности всей цепи ; активную P , реактивную Q и полную S мощности цепи. Задачу решить методом разложения токов на активные и реактивные составляющие. Построить векторную диаграмму токов в масштабе mi=2 А/см. Вычислить активную g и реактивную bc проводимости второй ветви.

  Дано : R1=12 Ом ; XL=9 Ом ; R2=12 Ом ; XC=16 Ом ; U=220 В.

  Найти : I1 , I2 , I , cosφ , P , Q , S , g2 , bc.

                                                                    Решение.

  Схема цепи изображена на рисунке.

 

  Находим полные сопротивления параллельных ветвей.

  Z1==15 Ом  ;  Z2= =20 Ом.

  Находим токи в параллельных ветвях : I1=U/Z1=220/15=14.7 A  ;  I2=U/Z2=220/20=11 A

  Найдём углы сдвига фаз между токами I1 и I2 и напряжением U.

  φ1=arctg[XL/R1]=arctg[9/12]=37°

  φ2=arctg[-XC/R2]=arctg[-16/12]=-53°

  Находим активные составляющие токов I1, I2 и I.

  Ia1=I1cosφ1=14.7×cos(37°)=11.7 A  ;  Ia2=I2cosφ2=11×cos(-53°)=6.6 A ;

  Ia=Ia1+Ia2=11.7+6.6=18.3 A

  Находим реактивные составляющие токов I1 , I2 и I.

  Ip1=I1sinφ1=14.7×sin(37°)=8.84 A  ;  Ip2=I2sinφ2=11×sin(-53°)=-8.78 A

  Ip=Ip1+Ip2=8.84-8.78=0,06 А

  Полный ток в неразветвленной части цепи : I==18.3 A.

  Найдём коэффициент мощности цепи : cosφ=Ia/I=18.3/18.3=1

  В цепи имеет место резонанс токов.

  Найдём активную P, реактивную Q и полную S мощности цепи.

  P=I12R1+I22R2=14.72×12+112×12=4045.08 Вт

  Q=I12XL-I22XC=14.72×9-112×16=8.8 вар

  S=UI=220×18.3=4026 В∙А , или  S==4045 В∙А.

  Вычислим активную g2 и реактивную bc составляющие второй ветви.

  g2=R2/Z22=12/202=0.05 сим ;  bc=-XC/Z22=-16/202=-0.04 сим.

 Для построения векторной диаграммы найдём длины векторов :

  ℓIa1=Ia1/mI=11.7/2=5.9 см ; ℓIp1=Ip1/mI=8.84/2=4.4 см ; ℓI1=I1/mI=14.7/2=7.4 см ;

  ℓIa2=Ia2/mI=6.6/2=3.3 см ; ℓIp2=Ip2/mI=8.78/2=4.4 см ; ℓI2=I2/mI=11/2=5.5 см.

  ℓIa=Ia/mI=18.3/2=9.2 см ; ℓIp=Ip/mI=0.06/2=0.03 см ; ℓI=I/mI=18.3/2=9.2 см.

  Построение векторной диаграммы начинаем с построения вектора напряжения U , который откладываем горизонтально. Вектор тока Ia1 откладываем параллельно вектору напряжения U. От конца вектора Ia1 откладываем вектор тока Ip1 перпендикулярно вектору U в сторону отставания от него. Геометрическая сумма векторов Ia1 и Ip1 дают вектор I1. Вектор тока Ia2 откладываем параллельно вектору напряжения U. От конца вектора Ia2 откладываем вектор тока Ip2 перпендикулярно вектору напряжения U в сторону его опережения. Геометрическая сумма векторов Ia2 и Ip2 дают вектор I2. Вектор I строим как геометрическая сумма векторов I1 и I2 , или как геометрическую сумму векторов Ia и Ip.

 

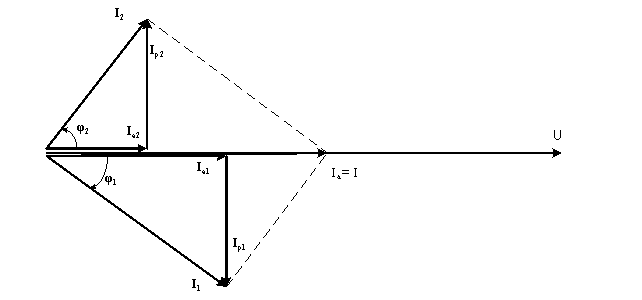
  Ответ : I1=14.7 A ; I2=11 A ; I=18.3 A ; cosφ=1 ; P=4045 Вт ; Q=8.8 вар ; S=4045 В∙А ; g2=0.05 сим ; bc=-0.04 сим.

 

 

 

 

  № 21

  Три одинаковых приёмника с сопротивлениями ZA=ZB=ZC=12+j16 Ом, соединены звездой и питаются от трёхфазной сети с линейным напряжением Uл=220 В. Начертить схему цепи. Определить фазное напряжение Uф ; фазные Iф и линейные Iл токи ; полную S , активную P и реактивную Q мощности ; коэффициент мощности cosφ трёхфазного потребителя. Построить в масштабе mu=40 В/см , mI=2 А/см векторную диаграмму напряжений и токов.

  Дано : ZA=ZB=ZC=12+j16 Ом ; Uл=220 В

  Найти : Uф , Iф , Iл , S , P , Q , cosφ.

                                                                     Решение.

 

  Так как приёмник симметричный, то полное сопротивление фаз :

  Z=ZA=ZB=ZC===20 Ом.

  Фазное напряжение : Uф=Uл/=220/=127 В

  Так как приёмник соединён звездой, то фазные и линейные токи равны :

  Iф=Iл=Uф/Z=127/20=6.35 А.

  Коэффициент мощности цепи : cosφ=R/Z=12/20=0.6 ; угол сдвига фаз между током Iф и напряжением Uф : φ=arccos(0.6)=53°

  Активная мощность цепи : P=3Iф2R=3×6.352×12=1452 Вт.

  Реактивная мощность цепи : Q=3Iф2X=3×6.352×16=1935 вар

  Полная мощность цепи : S==2419 В∙А.

  Для построения векторной диаграммы найдём длины векторов :

  ℓUф=Uф/mu=127/40=3.2 см  ;  ℓIф=Iф/mI=6.35/2=3.2 см.

  Построение диаграммы начинаем с построения векторов фазных напряжений UA, UB и UC , которые откладываем под углом 120° относительно друг – друга, предварительно отложив вектор UA вдоль вещественной оси.

  Вектора фазных токов откладываем под углом φ=53° от соответствующих фазных напряжений. Соединив концы векторов фазных напряжений, получим треугольник линейных напряжений.

 

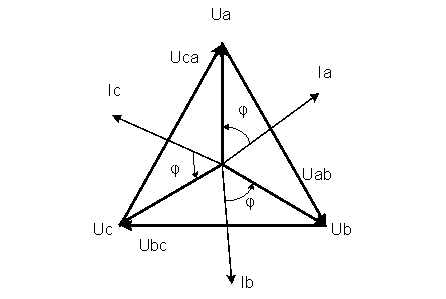
  Ответ : Uф=127 В ; Iф=6,35 А ; S=2419 В∙А ; P=1452 Вт ; Q=1935 вар ; cosφ=0.6.

  

 

 

 

  № 30

  Конденсатор С=30 мкФ, соединённый последовательно с резистором R=0.5 МОм, заряжается от сети с постоянным напряжением U=220 В. Определить постоянную времени цепи τ и значение разрядного тока и напряжения в конденсаторе для моментов времени t=0, τ, 2τ, 3τ, 4τ, 5τ. Начертить схему цепи. Построить в масштабе кривые iзар=f(t) ; uc=f(t).

  Дано : С=30 мкФ ; R=0.5 МОм ; U=220 В.

  Найти : τ ; iзар=f(t) ; uc=f(t).

                                                                      Решение.

 

 

  Постоянная времени цепи : τ=RC=0.5×106×30×10-6=15 c

  Напряжение на конденсаторе при заряде : uc=U(1-e-t/τ)=220(1-e-t/τ) В

  Вычислим значение напряжения на конденсаторе в моменты времени : t=0, τ, 2τ, 3τ, 4τ, 5τ. Вычисления сведём в таблицу.

 

t, c	0	τ	2τ	3τ	4τ	5τ
e-t/τ	1	0.37	0.14	0.05	0.02	0.01
uc , В	0	138.6	189.2	209	215.6	217.8

  По результатам расчёта строим кривую : uc=f(t).

 

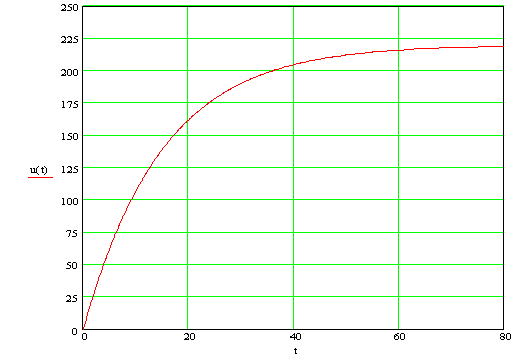
Ток переходного режима, или зарядный ток : i=Ie-t/τ===440e-t/τ мкА

  Вычислим значение зарядного тока в моменты времени : t=0, τ,2τ, 3τ, 4τ, 5τ.

  Вычисления сведём в таблицу.

 

t, c	0	τ	2τ	3τ	4τ	5τ
e-t/τ	1	0,37	0,14	0,05	0,02	0,01
I, мкA	440	162,8	61,6	22	8,8	4,4

 По результатам расчёта строим кривую : i=440e-t/τ мкА.

 

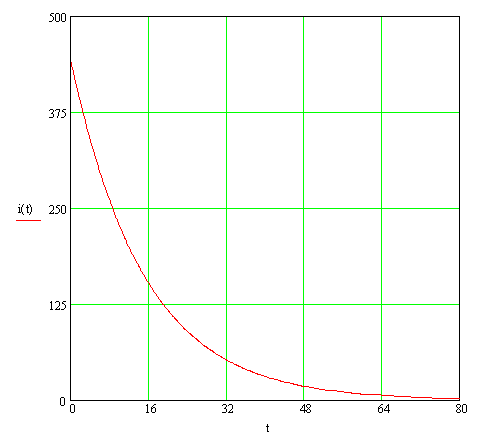
  Ответ : τ=15 с ; uc=220(1-e-t/τ) В ; i=440e-t/τ мкА.