Пример решения контрольной на тему "Синтез зубчатого механизма"

Ниже приведен текст пояснительной записки. Закачка полного решения(записка в doc и чертеж в формате cdw) начнется через 10 секунд.

СИНТЕЗ ЗУБЧАТОГО МЕХАНИЗМА

 

Расчет геометрических параметров цилиндрической зубчатой передачи

 

Исходные данные:

z1 = 12; z2 =24; m = 10 мм; x1 = 0,4; x2 = 0,4, α = 20°; ha* = 1; c* = 0,25,

где z1 и z2 - число зубьев шестерни и колеса соответственно;

m - модуль зубчатого зацепления;

x1 и x2  - коэффициенты смещения;

- угол главного профиля, градус;

ha* - коэффициент высоты головки зуба;

c* - коэффициент радиального зазора.

 

1.  Коэффициент суммы смещений xΣ:

xΣ = x1 + x2;

xΣ = 0,4 + 0,4 = 0,8.

 

2. Угол зацепления αw:

 

invαw = invα + (2xΣtgα)/zΣ;

 

invαw = inv20o + (2 . 0,8tg20o)/36; invαw = 0,031

 

Угол αw найдем по таблицам эвольвентной функции или из соотношения

 

invαw = tg αw – αw,

 

где αw подставляется в радианах, αw = 25,3°.

 

3.  Межосевое расстояние aw

 

aw = mzΣ(cosα / cosαw) / 2;

 

aw = 10 · 36 (cos20o / cos25,3o) / 2 = 187,1 мм.

 

4.  Делительные диаметры:

di = mzi;

d1 = m z1 = 10 · 12 = 120 мм;

d2 = m z2 = 10 · 24 = 240 мм.

 

5. Делительное межосевое расстояние:

а = (d1 +d2) / 2;

a = (120 + 240) / 2 = 180 мм.

 

 

6. Коэффициент воспринимаемого смещения:

y = (aw – a) / m;

y = (187,1 – 180) / 10 = 0,71

 

7. Коэффициент уравнительного смещения:

y = xΣ – y;

y =0,8 – 0,71 = 0,09

 

8. Радиусы начальных окружностей:

rw = (mz·cosα/cosαw) / 2;

rw1 = (10·12 cos20o/cos25,3o) / 2 = 62,36 мм;

rw2 = (10 · 24 cos20o/cos25,3o) / 2 = 124,74 мм.

 

Проверка вычислений

aw = rw1 + rw2;

aw = 62,36 + 124,74 = 187,1 мм.

 

9. Радиусы вершин зубьев:

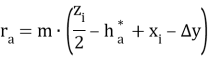
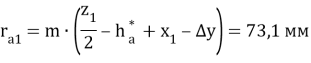
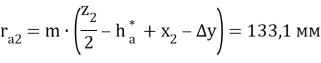
10.          Радиусы впадин:

 

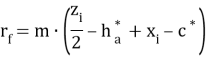
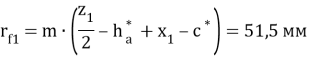
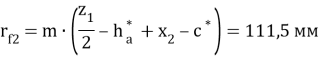
11.          Высота зубьев:

h = 73,1 – 51,5 = 133,1 – 111,5 = 21,6 мм.

12. Толщина зубьев по дуге делительной окружности:

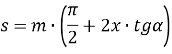
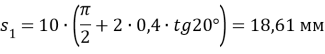
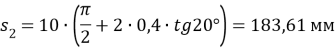
13. Радиусы основных окружностей:

rb1 = r1cosα = 56,4 мм;

rb2 = r2 cosα = 112,8 мм.

 

 

14. Углы профиля в точках на окружности вершин:

αa1 = arccos(rb1 /ra1) = 39,5o;

αa2 = arccos(rb2 / ra2) = 32,1o.

 

15. Толщина зубьев по дуге окружности вершин:

Sa1 = (mcosα) / cosαa1 [π / 2 + 2x1 tgα – z1· (invαa1 – invα)];

Sa2 = (mcosα) / cosαa2 [π / 2 + 2x2 tgα – z2· (invαa2 – invα)];

Sa1 = 5,12 мм; Sa2 = 6,76мм.

 

16. Коэффициент толщины зубьев по окружности вершин:

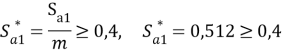
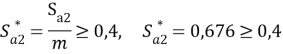
17. Коэффициент торцевого перекрытия:

 

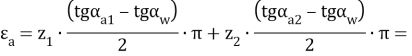
Сравнение εα с допускаемым [εα] = 1,2 показывает, что εα > [εα], следовательно, расчет произведен верно.

 

18. Масштаб длины μl для построения картины эвольвентного зацепления:

µl = aw / O1O2 = 0,1871 / 374,2 = 0,0005 м/мм,

где О1О2 – построенное на чертеже расстояние между центрами ко-лес, мм;

aw – межосевое расстояние, м.

 

Построение станочного зацепления

 

Профиль зуба нарезаемого колеса образуется как огибающая ряда положений исходного производящего контура реечного инструмента станочном зацеплении. При этом прямолинейная часть профиля инструмента образует эвольвентную часть зуба нарезаемого колеса, а закругленный участок – переходную кривую.

Построение станочного зацепления производим в том масштабе, чтобы высота зуба была не менее 50…70 мм, в следующей последовательности:

1. Проводим из выбранного центра О делительную и основную окружности, окружности вершин и впадин.
2. Касательно в точке Р0 к делительной окружности (она является начальной в станочном зацеплении) проводим начально-станочную прямую           Q – Q.
3. На расстоянии χ = x1m от начально-станочной прямой проводим делительную прямую исходного производящего контура.
4. Отложим по обе стороны делительной прямой расстояние, равное ha*m и от него (ha* + c*) m и проводим прямые граничных точек вершин и впадин.
5. Через полюс зацепления Р0 касательно к основной окружности проводим линию станочного зацепления P0N и P0N’. Эти линии образуют с прямыми участками исходного производящего контура углы, равные α0.

6. Построим исходный производящий контур таким образом, чтобы ось симметрии впадины проходила через точку Р0, а боковые стороны впадины были перпендикулярны линиям зацепления Р0N и P0N’. Для этого от точки G пересечения оси нарезаемого колеса с делительной прямой отложим в обе стороны отрезки в 0,25 шага.
7. Построим закругленные участки профиля как сопряжение прямолинейной части контура с прямыми вершин и впадин окружностью радиуса
8. По обе стороны от впадин построим по 1 – 2 зуба исходного производящего контура.
9. Для построения эвольвентного профиля зуба нарезаемого колеса на окружности вершин отложим толщину зуба Sa1. Обозначить точки А и А’.
10. Пересечения линий станочного зацепления с прямыми участками профиля инструмента обозначить точками K и K’.
11. На делительной окружности отложим толщину зуба S1 - получим точки В, В’.
12. По лекалу плавно соединяем точки А, В, К и А’, K’, В’.
13. Построим ножку зуба по прямой линии от точек В и В’ до прямой граничных точек.
14. Выполним сопряжение радиусом ρ линии профиля ножки зуба с окружностью впадин.
15. По трафарету построим еще не менее двух зубьев нарезаемого колеса, для чего проводим оси симметрии зубьев на расстоянии шага по хорде делительной окружности р1 или на расстоянии углового шага τ1 = 360o / z1.

При правильном построении профили зубьев нарезаемого колеса должны касаться прямолинейной части профиля инструмента в точках К и К’ на линии зацепления.

 

Построение картины эвольвентного зацепления

 

Построение зацепления пары зубчатых колес (рис. 5.2) производим в том же масштабе, что и станочное зацепление (см. рис. 5.1). Его проводим в следующей последовательности:

в     Отложим межосевое расстояние аw. При этом центры шестерни станочном и зубчатом зацеплениях могут совпадать, что является наиболее удобным.

2. Проводим все окружности колес: делительные (d), начальные (dw), основные (db), впадин (df) и вершин (da). При этом начальные окружности должны касаться друг друга в полюсе зацепления Р, делительные – отстоять друг от друга на величину воспринимаемого смещения y·m, а зазор между окружностью вершин одного колеса и окружностью впадин другого должен составить c*m.
3. Проводим касательно в точках N1 и N2 к основным окружностям линию зацепления, которая проходит через полюс Р и составляет угол зацепления аtw с касательной к начальным окружностям.
4. Через полюс зацепления Р построим по шаблону зуб шестерни.
5. Для построения профиля зуба колеса разделим расстояние PN2 на равные части длиной 10…15 мм и отложим такие же отрезки на линии зацепления за точкой N2.
6. Отложим от точки N2 такие же отрезки по дуге основной окружности и построим касательные к основной окружности, перпендикулярные соответствующим лучам, проведенным из центра, перпендикулярные соответствующим лучам, проведенным из центра О2.
7. На построенных касательных отложим соответствующее число отрезков и полученные точки соединим плавной кривой. Это и будет эвольвентный участок профиля зуба.

8. Обозначим активную длину зацепления АВ, расположенную на линии зацепления между точками ее пересечения с окружностью вершин.
9. Построим положения профилей зубьев колеса и шестерни в точках             А и В начала и конца зацепления и замерим угол перекрытия, соответствующий дуге окружности, отсекаемой этими профилями. Проверим рассчитанную величину коэффициента перекрытия

εα = φγ1 / τ1 = φγ2 / τ2.

10. Указываем активные рабочие участки профилей зубьев, расположенные между вершиной зуба одного колеса и точкой, сопряженной вершиной зуба другого колеса.
11. Проставим на чертеже все необходимые геометрические размеры пары зацепляющихся колес.

 

Библиографический список

 

1. Теория механизмов и механика машин: учеб. для вузов/ [ К.В.Фролов и др.] ; под ред. Г.А. Тимофеева. – 7-е изд. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2012. – 686 с.: ил. – (Механика в техническом университете).

2. Артоболевский И.И. Теория механизмов: учеб. для технических вузов. – 2-е изд. – М.: Наука, 1967. – 720 с.: ил.

3. Белан А.К., Белан О.А. Задания для выполнения курсового проекта по дисциплинам «Теория механизмов и машин» и «Прикладная механика» для специальностей 150201, 151001, 150401, 190205, 190603. Ч.1. – Магнитогорск: ГОУ ВПО «МГТУ», 2009. – 34 с.

4. Попов С.А., Тимофеев Г.А. Курсовое проектирование по теории механизмов и механике машин: учеб. пособие для ВТУЗов / Под ред. К.В. Фролова. – 2-е изд. – М.: Высшая школа, 1998. – 351 с.: ил.