Регрессионный анализ в Excel

Ниже приведены условия задач, и текстовый отчет о решении. Закачка полного решения(документы  doc и xlsx в архиве zip) начнется автоматически через 10 секунд. 

Задача 1. По данным приведенным в таблице 1 провести регрессионный анализ, используя следующие зависимости: линейную, квадратическую, гиперболическую, показательную, степенную, логарифмическую. Выбрать лучшую модель.

Таблица 1 – Исходные данные

№ п/п	X	Y
1	1	12
2	2	18
3	3	15
4	4	25
5	5	26
6	6	34
7	7	37
8	8	47

 

Решение.

Для решения поставленной задачи и упрощения расчетов воспользуемся средствами табличного процессора MS Excel.

Первым этапом будет ввод исходных данных и построение линейной модели регрессии.

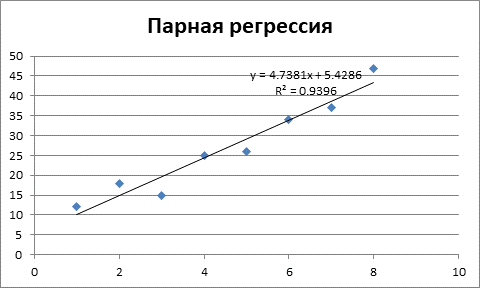
Рисунок 1 – Получение параметров линейной модели регрессии.

Таким образом, получили следующее линейное уравнение регрессии:

На рисунке 1 показано значение коэффициента детерминации R² = 0,94. То есть 94% значений переменной Y объясняется значениями переменной X. Таким образом, можно говорить о высоком качестве уравнения регрессии.

Следующим этапом будет построение квадратического уравнения регрессии.

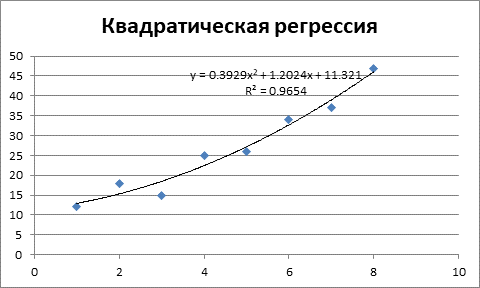
Рисунок 2 – Квадратическое уравнение регрессии и коэффициент детерминации.

Как видим из рисунка 2, коэффициент детерминации составляет R² = 0,9654, то есть качество уравнения несколько выше линейного уравнения.

Следующим этапом будет получение показательного уравнения регрессии.

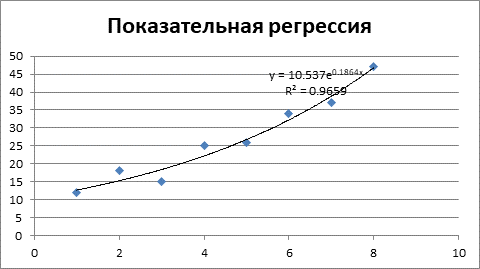
Рисунок 3 – Показательная регрессия и коэффициент детерминации.

Уравнение показательной регрессии объясняет 94,06% значений зависимой переменной Y от факторной переменной X.

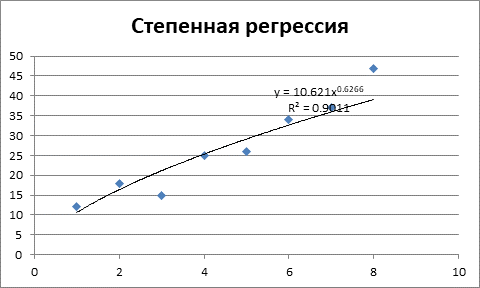
Рисунок 4 – Степенная регрессия и коэффициент детерминации.

Согласно рис. 4 полученное уравнение регрессии объясняет 87,7% значений зависимой переменной Y. Данное уравнение достаточно хуже по качеству, чем предыдущие.

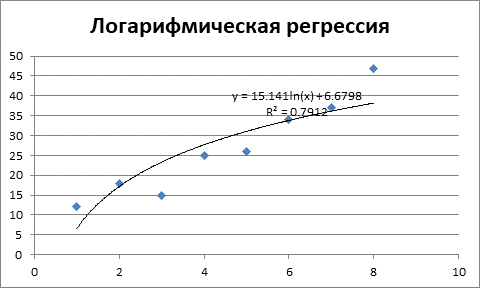
Рисунок 5 – Логарифмическая регрессия и коэффициент детерминации

Коэффициент детерминации логарифмического уравнения регрессии говорит о достаточно хорошем качестве уравнения регрессии, однако оно уступает по качеству предыдущим уравнениям.

В заключении строим график гиперболической регрессии.

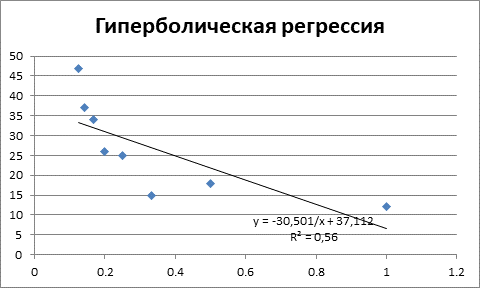
Рисунок 6 – Гиперболическая регрессия и коэффициент детерминации

Как видим данное уравнение регрессии является наихудшим по качеству, поскольку объясняет только 56% значений зависимой переменной Y.

Наилучшим по качеству уравнением регрессии в данной задаче является уравнение квадратической регрессии. Данное уравнение объясняет 96,54% значений зависимой переменной Y.

 

Задача 2. По данным приведенным в таблице 2 требуется:

1. Построить линейное уравнение регрессии Y по X.

2. Рассчитать линейный коэффициент корреляции, коэффициент детерминации и среднюю ошибку аппроксимации.

3. Рассчитать коэффициент эластичности.

Таблица 2 – Исходные данные

№ п / п	X	Y
1	10	33
2	9	40
3	9	20
4	7	34
5	9	35
6	12	44
7	10	37
8	6	30

 

Решение.

Для решения поставленной задачи воспользуемся средствами табличного процессора MS Excel.

Для этого создаем новый лист и вводим исходные данные

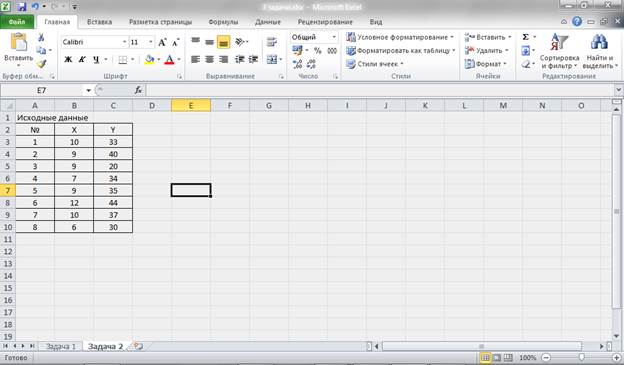
Рисунок 7 – Исходные данные.

Уравнение парной регрессии имеет вид:

- x, y – факторная и зависимые переменные;

- a, b – коэффициенты уравнения.

Коэффициенты уравнения парной линейной регрессии будем искать с помощью метода наименьших квадратов и табличного процессора MS Excel. Согласно МНК коэффициенты уравнения находятся по следующим формулам:

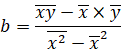
Составим дополнительную таблицу и произведем промежуточные расчеты в табличном процессоре:

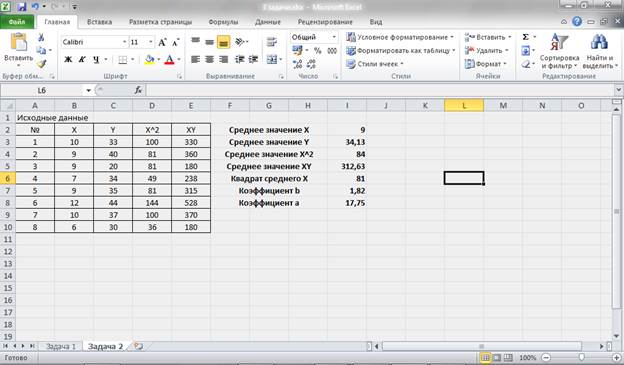
Рисунок 8 – Промежуточные расчеты и расчет коэффициентов уравнения.

В результате мы получили уравнение парной линейной регрессии:

Коэффициент корреляции, как правило используется для оценки направления и тесноты связи между зависимой и факторной переменными. Однако уже сейчас мы можем предположить направление связи между X и Y по знаку в уравнении регрессии.

Поскольку в уравнении стоит знак «+», то можно предположить наличие прямой связи между X и Y, т.е. значения Y напрямую зависят от значений X.

С помощью средств табличного процессора оценим тесноту этой связи:

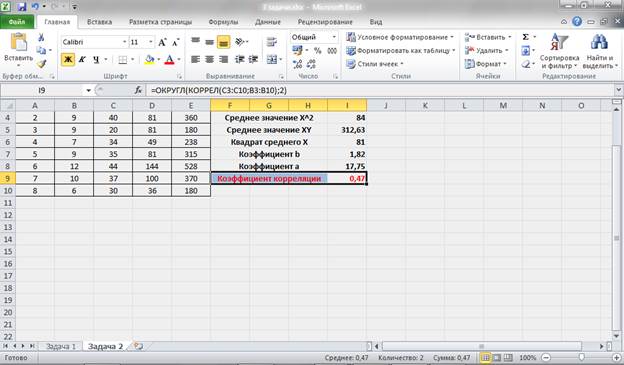
Рисунок 9 – Оценка тесноты связи с помощью коэффициента корреляции.

Коэффициент корреляции r_yx = 0,47. Отсюда можно сделать вывод, что между переменными X и Y существует умеренная связь. Положительное значение коэффициента корреляции подтверждает наше предположение о направлении связи – Y зависит от X.

Между коэффициентом корреляции и коэффициентом детерминации существует взаимосвязь:

Отсюда получаем значение коэффициента детерминации: R² = 0,22. То есть уравнение регрессии объясняет 22% значений зависимой переменной. Можно говорить о невысоком качестве уравнения регрессии.

Для подтверждения наших выводов о качестве уравнения рассчитаем показатель средней ошибки аппроксимации:

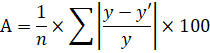
Проведем дополнительные расчеты:

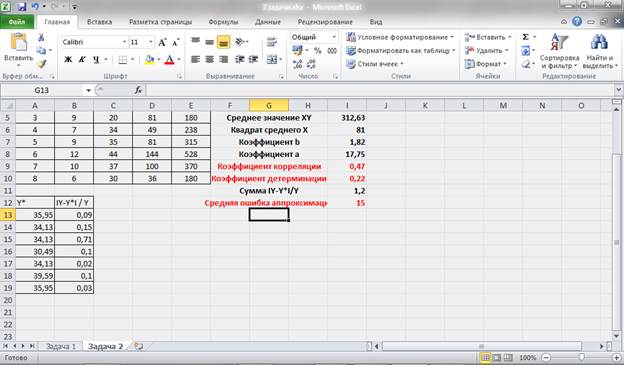
Рисунок 10 – Промежуточные расчеты и расчет средней ошибки аппроксимации.

Получаем, что средняя ошибка аппроксимации не попадает в предел до 5 – 8% (А = 15%), что подтверждает наш вывод о невысоком качестве уравнения регрессии.

Коэффициент эластичности определим по следующей формуле:

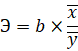
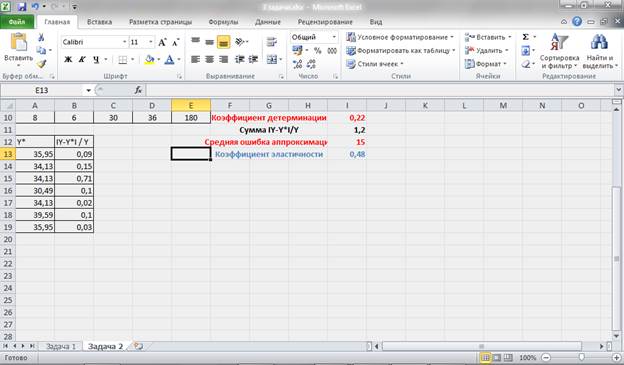
Рисунок 11 – Расчет коэффициента эластичности.

Таким образом, при изменении значения Х на 1% значение Y изменится на 0,48%.

 

Задача 3. По данным приведенным в таблице 3 требуется:

1. Построить линейную модель множественной регрессии.

2. Записать стандартизированное уравнение множественной регрессии.

3. Рассчитать коэффициенты парной, частной и множественной корреляции. Проанализировать их.

Таблица 3 – Исходные данные

№ п / п	Х1	X2	Y
1	12	12	133
2	8	22	135
3	8	15	120
4	7	19	125
5	9	17	130
6	10	11	144
7	7	10	137
8	9	28	121

 

Решение.

Для решения поставленной задачи используем возможности и средства табличного процессора MS Excel. Вводим исходные данные.

Для построения модели множественной регрессии проведем дополнительные расчеты:

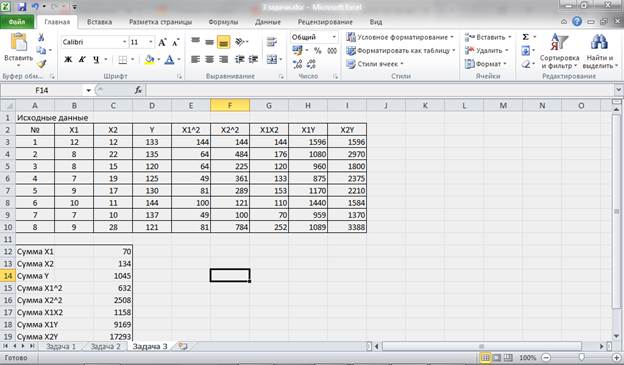
Рисунок 12 – Промежуточные расчеты.

Параметры уравнения множественной регрессии для двухфакторной модели можно определить из системы уравнений:

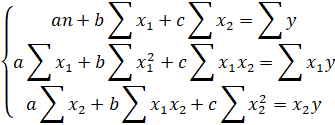
Запишем действующую систему уравнений:

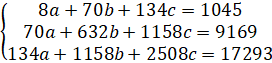
Данную систему можно решить методом Крамера при условии, что матрица, составленная из коэффициентов при неизвестных, не являтся вырожденной, т.е. Δ ≠ 0.

Для упрощения вычислений рассчитываем определитель матрицы, составленной из коэффициентов при неизвестных:

Δ = 39 424

Поскольку исходная матрица не является вырожденной система уравнений имеет решение.

Δ₁ = 5 399 564

Δ₂ = 28 780

Δ₃ = -29 948

Отсюда находим коэффициенты при неизвестных в уравнении регрессии:

- a = 136,96

- b = 0,73

- c = -0,76.

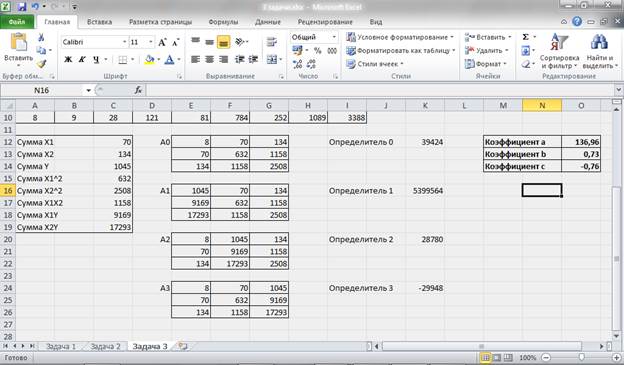
Рисунок 13 – Расчет параметров уравнения множественной регрессии.

Таким образом, мы получаем следующее уравнение множественной регрессии:

Для построения уравнения множественной регрессии в стандартизированной форме проведем расчет стандартных ошибок и коэффициентов стандартизированного уравнения:

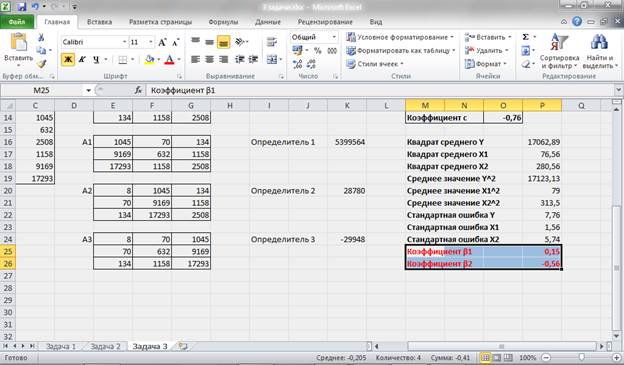
Рисунок 14 – Расчет коэффициентов стандартизированного уравнения.

Таким образом, стандартизированное уравнение множественной регрессии примет вид: t_y = 0,15t_x1 – 0,56t_x2

Для расчета парной, частной и множественной корреляции воспользуемся таким инструментом табличного процессора, как пакет анализа, для построения корреляционной матрицы:

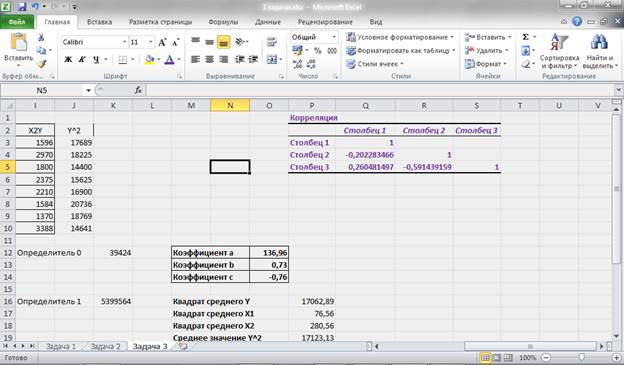
Рисунок 15 – Расчет корреляционной матрицы.

Как видим из рис. 15. Наибольшая связь обратного направления присутствует между переменными Y и X₂, т.е. по сути Х₂ зависит от значений Y. Прямая же связь между Y и X₁ хоть и присутствует, но она достаточно слабая.

Также присутствует слабая обратная связь между переменными X₁ и X₂.

 

 

 

 

 

 

 

 

 

 

 

Список литературы

Список литературы

1.                Айвазян С.А., Мхитарян В.С. Прикладная статистика и основы эконометрики. Учебник для вузов. – М.ЮНИТИ, 1998. – с. 621 – 632; 751 – 766.

2.                Бородич С.А. Эконометрика: Учебное пособие. – Мн.: Новое знание, 2001. – с. 98 – 115; 121 – 147; 200 – 222

3.                Доугерти К. Введение в эконометрику: Пер. с англ. – М.: ИНФРА-М, 1999. – XIV, с. 53 – 111

4.                Кремер Н.Ш., Путко Б.А. Эконометрика: Учебник для вузов / Под ред. Проф. Н.Ш. Кремера. – М.: ЮНИТИ-ДАНА, 2002. – с. 50 – 80

5.                Кулинич Е.И. Эконометрия. – М.: Финансы и статистика, 2001. с. 43 – 83

6.                Магнус Я.Р., Катышев П.К., Пересецкий А.А. Эконометрика. Начальный курс. Учебное пособие. 2-е изд. – М.: Дело, 1998. – с. 17 – 42

7.                Практикум по эконометрике: Учебное пособие / И.И. Елисеева, С.В. Курышева, Н.М. Гордеенко и др.; Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2002. – с. 5 – 48