Построение уравнения множественной регрессии со всеми факторами матричным методом и с помощью надстройки «Анализ данных» MS Excel.

Ниже приведены условия задач, и текстовый отчет о решении. Закачка полного решения(документы  doc и xlsx в архиве rar) начнется автоматически через 10 секунд. 

Классическая линейная модель множественной регрессии

Цель работы

Изучить основные методы построения КЛММР и ее использования.

Исходные данные

 

 

 

Ход работы

1) Построим уравнение множественной регрессии со всеми факторами матричным методом и с помощью надстройки «Анализ данных» ППП MS Excel.

Матричный метод

Определим вектор оценок коэффициентов регрессии. Согласно методу наименьших квадратов, вектор s получается из выражения:
К матрице с переменными  добавляем единичный столбец:

Сначала умножаем транспонированную матрицу на у:

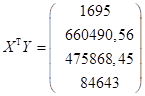
Потом также умножаем транспонированную матрицу на х :

;  

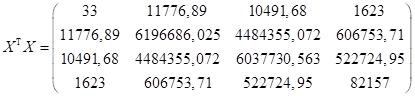Находим обратную к полученной матрице:

 

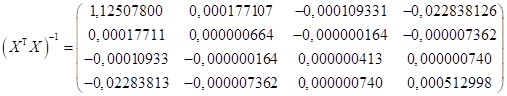
Уравнение регрессии в матричном виде тогда будет иметь вид:

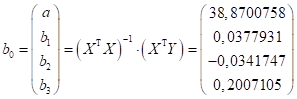
Оценка дисперсии равна:

Уравнение регрессии в скалярном виде:

 

 

Построение модели с помощью надстройки «Анализ данных» ППП MS Excel

Для построения уравнения линейной регрессии используем функцию «Данные»  «Анализ данных»  «Регрессия» табличного процессора MS Excel

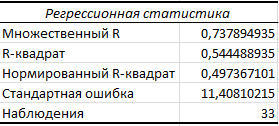
Уравнение множественной регрессии имеет вид:

Оценка дисперсии равна:

3) Проверка факторов на наличие коллинеарности. Отбор неколлинеарных факторов.

Построим корреляционную матрицу, используя функцию «Данные»  «Анализ данных»  «Корреляция» табличного процессора MS Excel.

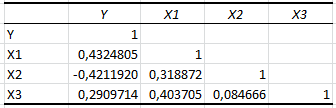
Проводим анализ коэффициентов корреляции

– связь прямая и умеренная;

 – связь обратная и умеренная;

 – связь прямая и слабая;

 – связь прямая и умеренная;

 – связь прямая и умеренная;

 – связи практически нет.

Ни один коэффициент межфакторной корреляции не превышает 0,6, следовательно, мультиколлинеарности не наблюдается.

Значение коэффициента корреляции между Y и Х₃ незначительно, связь слабая следовательно, фактор Х₃ признается незначимым.

4) Оценка качества модели

Определение значений коэффициента множественной корреляции и коэффициента детерминации.

Значения берем из протокола регрессионного анализа:. Связь результативного признака Y со всеми факторными признаками  высокая.

Коэффициент детерминации равен . Следовательно, 54,45% вариации признака Y объясняется вариацией признаков Х₁, Х₂, и Х₃, остальные 45,55% вариацией других признаков, не включенных в модель.

Проверка значимости уравнения при заданном уровне значимости.

Значения берем из протокола дисперсионного анализа

Значимость уравнения проверим с помощью критерия Фишера:

Табличное значение при уровне значимости 5% и степенях свободы   равно:

Так как наблюдаемое значение критерия Фишера больше табличного, уравнение признается значимым.

Проверка значимости коэффициентов уравнения при заданном уровне значимости.

Значения берем из протокола регрессионного анализа

Для начала вычислим табличное значение t-статистики при уровне значимости 5%

и количестве степеней свободы 29: .

Находим t-статистики для параметров уравнения:

Параметр признается значимым, если значение его t-статистики больше табличного

 

 

Доверительные интервалы для коэффициентов берем из протокола регрессионного анализа.

 

Из результата видно, что в доверительный интервал коэффициента при Х3 входит 0. Это еще раз подтверждает, что параметр не значим.

5) Определение частных коэффициентов эластичности.

 

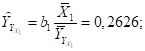
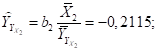
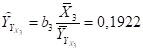
·         при увеличении фактора Х₁ на 1% результат Y увеличивается на 0,2626%;

·         при увеличении фактора Х₂ на 1% результат Y уменьшается на 0,2115%;

·         при увеличении фактора Х₃на 1% результат Y увеличивается на 0,1922%;

Максимальное значение коэффициента эластичности по модулю  следовательно, фактор Х₁ оказывает наибольшее влияние на результат.

6) Построим и проанализируем другие модели с различным количеством регрессоров.

Построение уравнения линейной множественной регрессии с учетом только значимых факторов (Х₁ и Х₂).

Определим значения коэффициента множественной корреляции и коэффициента детерминации.

Коэффициент корреляции:. Связь результативного признака Y со всеми факторными признаками высокая.

Коэффициент детерминации . Следовательно, 53,5% вариации признака Y объясняется вариацией признаков  Х₁ и Х₂, остальные 46,5% вариацией других признаков, не включенных в модель.

Значимость уравнения проверим с помощью критерия Фишера:  . Табличное значение при уровне значимости 5% и степенях свободы  ; равно: .

Так как наблюдаемое значение критерия Фишера больше табличного, уравнение признается значимым.

Значимость коэффициентов уравнения при заданном уровне значимости.

Для начала вычислим табличное значение t-статистики при уровне значимости 5%  и количестве степеней свободы 30: . Находим t-статистики для параметров уравнения:

 

Построение уравнения парной линейной множественной регрессии с учетом значимого фактора Х₁.

Определим значения коэффициента множественной корреляции и коэффициента детерминации.

Коэффициент корреляции: R=0,4325. Связь результативного признака Y с факторным умеренная.

Коэффициент детерминации . Следовательно, 18,7% вариации признака Y объясняется вариацией признаков  Х₁, остальные 81,3% вариацией других признаков, не включенных в модель.

Значимость уравнения проверим с помощью критерия Фишера:  . Табличное значение при уровне значимости 5% и степенях свободы  ; равно: .

Так как наблюдаемое значение критерия Фишера больше табличного, уравнение признается значимым.

Значимость коэффициентов уравнения при заданном уровне значимости.

Для начала вычислим табличное значение t-статистики при уровне значимости 5%  и количестве степеней свободы 31: . Находим t-статистики для параметров уравнения:

 

 

Построение уравнения парной линейной множественной регрессии с учетом значимого фактора Х₂.

Определим значения коэффициента множественной корреляции и коэффициента детерминации.

Коэффициент корреляции:. Связь результативного признака Y с факторным умеренная.

Коэффициент детерминации . Следовательно, 17,74% вариации признака Y объясняется вариацией признаков  Х₂, остальные 82,26% вариацией других признаков, не включенных в модель.

Значимость уравнения проверим с помощью критерия Фишера:  . Табличное значение при уровне значимости 5% и степенях свободы  ; равно: .

Так как наблюдаемое значение критерия Фишера больше табличного, уравнение признается значимым.

Значимость коэффициентов уравнения при заданном уровне значимости.

Для начала вычислим табличное значение t-статистики при уровне значимости 5%  и количестве степеней свободы 31: . Находим t-статистики для параметров уравнения:

 

8) Составим сравнительную таблицу моделей

Регрессия	Коэффициент корреляции	Коэффициент детерминации	F-критерий Фишера	Значимость параметров
				a0	b1	b2	b3
Y(X1;X2;X3)	0,7379	0,5350	11,5549	Значим	Значим	Значим	Не значим
Y(X1;X2)	0,7314	0,5350	17,2589	Значим	Значим	Значим	-
Y(X1)	0,4325	0,1870	7,1322	Значим	Значим	-	-
Y(X2)	0,4212	0,1774	6,6855	Значим	Значим	-	-

 

Из таблицы видно, что наибольшее коэффициента официанта корреляции у модели со всеми факторами. Однако параметрам b₃ в ней не значим. Поэтому наилучшей моделью признаётся уравнение с факторными переменными Х₁ и Х₂. У нее и также высокие коэффициенты корреляции и детерминации, наибольший критерий Фишера и все параметры значимы.

Интерпретация параметров модели Y(X₁;X₂) :

При увеличении фактора X₁ на единицу результат Y увеличивается на 0,407.

При увеличении фактора X₂ на единицу результат Y уменьшается на 0,0345.

9) Выполним прогноз

Для прогноза задаем вектор прогноза:

;

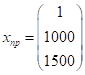Точечный прогноз: 

Ошибка прогноза:

;    

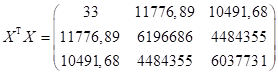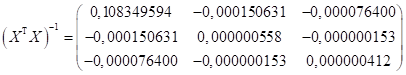
Умножаем матрицы  и :

 

Умножаем полученную матрицу на , находим:

Оценка дисперсии равна:

Несмещенная оценка дисперсии равна:

Оценка среднеквадратичного отклонения:

Доверительный интервал с вероятностью 0,95 для значения результативного признака: , где  находим по таблице Стьюдента.

Доверительный интервал:

или

C вероятностью 0.95 среднее значение при  находится в указанных пределах.

Доверительный интервал с вероятностью 0,95 для индивидуального значения результативного признака.

Доверительный интервал:

или

C вероятностью 0,95 индивидуальное значение при находится в указанных пределах.

 

 

 

Список литературы

1.      Доугерти К. Введение в эконометрику: Пер. с англ. – М.: ИНФРА-М, 2003. – 402 с.

2.      Кремер Н.Ш., Путко Б.А. Эконометрика: Учебник для вузов / Под ред. проф. Н.Ш. Кремера. – М.: ЮНИТИ-ДАНА, 2010. – 311 с.

3.      Магнус Я.Р., Катышев П.К., Пересецкий А.А. Эконометрика. Начальный курс: Учебник. – М.: Дело, 2007. – 400 с.

4.      Эконометрика: Учебник / Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2007. – 344 с.

5.      Эконометрика: Учебно-методическое пособие / Шалабанов А.К., Роганов Д.А. – Казань: ТИСБИ, 2005. – 56 с.