Контрольная работа по эконометрике в Excel

Ниже приведены условия задач, и текстовый отчет о решении. Закачка полного решения(документы  doc и xlsx в архиве rar) начнется автоматически через 10 секунд. 

1. Построение спецификации эконометрической модели 

Привести постановку задачи построения модели парной линейной регрессии. Выбрать эндогенную переменную. Сделать предположения относительно знаков (положительный или отрицательный) параметров модели.

2.                  Исследование взаимосвязи данных показателей с помощью диаграммы рассеяния и коэффициента корреляции

Построить график диаграммы рассеяния зависимой переменной с экзогенным фактором. Оценить коэффициент корреляции между объясняемой и объясняющей переменными. Проверить значимость коэффициента корреляции.

3.Оценка параметров модели парной регрессии

Оценить параметры модели (1) парной регрессии

  (1)

Выпишите полученное уравнение регрессии в стандартной форме. Дайте экономическую интерпретацию параметрам модели.

4.Оценивание качества спецификации модели

Проверить статистическую значимость регрессии в целом. Проверить статистическую значимость оценок параметров. Оценить точность модели с помощью средней относительной ошибки аппроксимации. Сделайте выводы   качестве уравнения регрессии.

5. Проверка предпосылки теоремы Гаусса-Маркова об отсутствии автокорреляции случайных возмущений

Привести результаты тестирования на отсутствие автокорреляции случайных возмущений с помощью теста Дарбина -Уотсона и Бреуша-Годфри.  Сделать выводы. При необходимости выполнить корректировку модели.

6. Множественная регрессия. Построение спецификации эконометрической модели множественной регрессии.

В связи с тем, что объясняющая переменная представляет собой временной ряд, одной из составляющих компонент которого может быть сезонная волна, необходимо учесть эту структуру для дальнейшего прогноза, вводя фиктивные переменные для соответствующих кварталов. Постройте график изменения     экзогенной переменной   во времени с целью визуального выявления сезонной волны.

 Введите необходимое количество фиктивных переменных, характеризующих степень влияния каждого квартала в отдельности.  Постройте многофакторную модель динамики     экзогенной переменной.

Оцените параметры модели (2) множественной регрессии

     (2)

 Оцените качество и значимость модели и отдельных ее параметров. Поясните экономический смысл параметров при фиктивных переменных сдвига при исследовании сезонных колебаний. Выполните тестирование на отсутствие автокорреляции случайных возмущений с помощью Бреуша-Годфри. 

7.                   Прогнозирование экзогенной переменной

Использовать построенную многофакторную модель с фиктивными переменными для прогнозирования экзогенной переменной.

Оценить прогноз   по модели (2)

 

Прогнозирование эндогенной переменной

Оценить прогноз по модели (1), используя полученные прогнозные значения  X

— прогноз значения эндогенной переменной для момента )

Подставив прогнозные значения  в модель (1), получим точечный прогноз :

                                                       

Построим интервальную оценку значения эндогенной переменной   на интервале прогнозирования для момента ,

 нижняя граница интервала прогнозирования;

— верхняя граница интервала прогнозирования;

— табличное значение критерия Стьюдента.

 – ошибка прогноза, вычисляется по формуле:

 , где   — p-я строчка матрицы регрессоров (прогнозные значения Х); s — стандартная ошибка модели (можно найти в первой таблице протокола регрессии).

Эта формула в случае модели парной регрессии может быть записана в виде:  .

Представить результаты моделирования и прогнозирования в графическом формате

ВАРИАНТ 17

Ставится задача исследовать, как влияет размер средней номинальной заработной платы (WAG_C_Q  в  руб.)  на среднедушевые денежные доходы населения (HHI_Q  в руб.) в России.  Денежная масса М0 — это совокупность наличных денег, находящихся в обращении в млрд. (трлн.) руб.   Данные с сайта http://sophist.hse.ru

T	Средняя номинальная заработная плата	Среднедушевые денежные доходы населения (HHI_Q)
2008 I	15424	9930,9
II	16962	11932,5
III	17556	12667,1
IV	18966	15605,9
2009 I	17441	12213
II	18419	14749,7
III	18673	15579,3
IV	20670	16904,5
2010 I	19485	14065,1
II	20809	16967,9
III	21031	16730,6
IV	23491	19833,3
2011 I	21354	16146,4
II	23154	18690
III	23352	18549,4
IV	26905	22456
2012 I	24407	17710,6
II	26547	20417,6
III	26127	20512,3
IV	30233	24535
2013 I	27339	19121
II	30245	22591
III	29578	23280,7
IV	33269	27986,2
2014 I	30057	21800
II	32963	24990,4
III	31730	25528,7
IV	35685	30532,9
2015 I	31566	22457,1
II	34703	27059,3
III	32983	27964,6
IV	35692	32285
2016 I	34000	25364
II	37404	29723,1
III	35744	29945,5
IV	39824	36099,8
2017 I	35983	26646,2
II	40103	30234
III	37723	30539,5
IV	42797	36149,5
2018 I	40691	27763
II	44477	31306,6
III	41830	31325
IV	46850	37224,6
2019 I	43944	29011,2
II	48453	32455
III	45726	32609,2
IV	51684	38945
2020 I	48390	30240,8
II	50784	34569,1
III	49021	35096,9
IV	56044	41428,3

 

Парная линейная регрессия определяется моделью вида:

В качестве эндогенной переменной будет выступать среднедушевые денежные доходы населения в России., а экзогенная - размер средней номинальной заработной платы.

В нашем случае

           

Исходя из экономического смысла модели можем предположить, что коэффициент регрессии  модели будет положительным

 

Строим диаграмму рассеяния зависимой переменной с экзогенным фактором

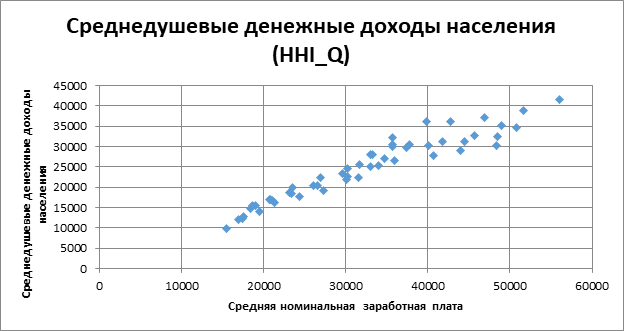
Вывод: Вытянутость облака точек на диаграмме рассеяния вдоль наклонной прямой позволяет сделать предположение, что существует некоторая объективная тенденция прямой линейной связи между значениями переменных x и y, т.е. в среднем, с увеличением размера средней номинальной заработной платы, в среднем увеличиваются среднедушевые денежные доходы населения

Чтобы вычислить корреляцию средствами Excel, воспользуемся функцией =КОРРЕЛ().

Получили  что свидетельствует о тесной прямой связи между факторами

Оценим значимость коэффициента корреляции. Для этого рассчитаем значение t – статистики по формуле

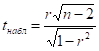
Критическое значение t – статистики Стьюдента получим с помощью
функции СТЬЮДРАСПРОБР пакета Excel.В качестве аргументов функции необходимо задать число степеней свободы равное n-2=52-2=50 и значимость  ( = 0,05).

Получили:

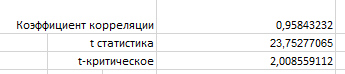
Сравнивая числовые значения критериев, видно, что |t_набл|=23,753> t_таб=2,01, т.е. полученное значение коэффициента корреляции значимо.

Вывод: размер средней номинальной заработной платы оказывает высокое влияние на среднедушевые денежные доходы населения, связь прямая.

 

Оценим параметры модели с помощью надстройки Excel Анализ данных, используя инструмент Регрессия.

Данные записать в таблицу Excel.

· Выбрать команду на вкладке Данные Þ команда Анализ данных.

· В диалоговом окне Анализ данных выбрать инструмент Регрессия.

· В диалоговом окне Регрессия в поле Входной интервал Y ввести адрес одного диапазона ячеек, который представляет зависимую переменную. В поле Входной интервал Х ввести адрес диапазона, который содержит значения независимой переменной

· Установить флажок Метки в первой строке для отображения заголовков столбцов.

· Выбрать параметры вывода.

· В поле Остатки и График подбора поставить флажки.

ОК

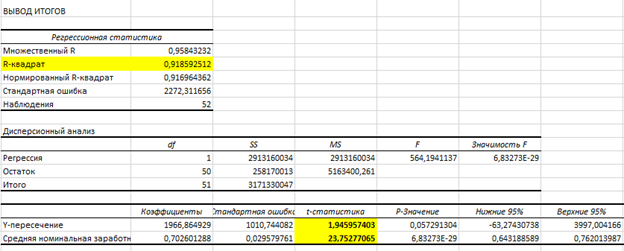
Получена модель

С ростом заявленной размера средней номинальной заработной платы на 1 руб.  среднедушевые денежные доходы населения увеличиваются на 0,7026 руб.

 

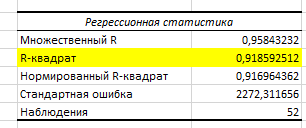
В качестве показателя степени влияния выбранного регрессора на поведение эндогенной переменной принимается коэффициент детерминации. Значение коэффициента детерминации можно найти в первой таблице протокола регрессионного анализа Регрессионная статистика

 

 

Для проверки значимости модели регрессии используется F-критерий Фишера. Значение F критерия можно найти в первой таблице протокола регрессионного анализа Дисперсионный анализ

Критическое значение F – статистики для параметров: ,

 и уровня значимости  равно , таким образом ,  и, следовательно, оцененная регрессия в целом статистически значима.

 

Значимость оценок параметров проверяется при помощи неравенства:

Воспользуемся значениями t-статистики полученными при проведении регрессионного анализа

 —  оценка  статистически  не значима при уровне значимости ,

 — оценка  статистически значима при уровне значимости .

Таким образом, регрессоры, включённые в спецификацию модели статистически значимо влияют на эндогенную переменную.

 

Промежуточные вычисления для получения средней относительной ошибки аппроксимации.

Наблюдение	Предсказанное Среднедушевые денежные доходы населения (HHI_Q)	Остатки	|e|/y
1	12803,7872	-2872,887199	0,289287698
2	13884,38798	-1951,88798	0,163577455
3	14301,73315	-1634,633145	0,12904557
4	15292,40096	313,4990384	0,020088495
5	14220,934	-2007,933997	0,164409563
6	14908,07806	-158,378057	0,010737714
7	15086,53878	492,7612158	0,031629227
8	16489,63356	414,8664433	0,024541775
9	15657,05103	-1591,95103	0,11318448
10	16587,29514	380,6048642	0,022430876
11	16743,27262	-12,67262178	0,000757452
12	18471,67179	1361,628209	0,068653639
13	16970,21284	-823,8128379	0,051021456
14	18234,89516	455,1048434	0,024350179
15	18374,01021	175,3897883	0,009455281
16	20870,35259	1585,647411	0,070611303
17	19115,25457	-1404,654571	0,079311518
18	20618,82133	-201,2213275	0,009855288
19	20323,72879	188,5712135	0,00919308
20	23208,60968	1326,390324	0,05406115
21	21175,28155	-2054,281548	0,107435885
22	23217,04089	-626,0408913	0,02771196
23	22748,40583	532,2941679	0,022864182
24	25341,70719	2644,492813	0,094492743
25	23084,95185	-1284,951849	0,058942745
26	25126,71119	-136,3111927	0,005454542
27	24260,4038	1268,296196	0,04968119
28	27039,1919	3493,708101	0,114424378
29	24145,17719	-1688,077193	0,075168975
30	26349,23743	710,0625658	0,026240981
31	25140,76322	2823,836782	0,10097898
32	27044,11011	5240,889892	0,162332039
33	25855,30873	-491,3087286	0,019370317
34	28246,96351	1476,136486	0,049662938
35	27080,64538	2864,854625	0,095668953
36	29947,25863	6152,541369	0,170431453
37	27248,56708	-602,3670831	0,022606116
38	30143,28439	90,71560948	0,00300045
39	28471,09332	2068,406675	0,067728898
40	32036,09226	4113,407739	0,113788787
41	30556,41395	-2793,413948	0,10061643
42	33216,46243	-1909,862425	0,061005105
43	31356,67682	-31,67681526	0,001011231
44	34883,73528	2340,864718	0,062884886
45	32841,97594	-3830,775939	0,132044725
46	36010,00515	-3555,005147	0,10953644
47	34094,01143	-1484,811434	0,045533513
48	38280,10991	664,8900907	0,017072541
49	35965,74127	-5724,941266	0,189311833
50	37647,76875	-3078,66875	0,0890584
51	36409,08268	-1312,182679	0,037387424
52	41343,45153	84,84847413	0,00204808
Сумма			3,581700319
Средняя ошибка аппроксимации			6,88788523

 

Воспользовавшись данными из табл., получим . Точность модели достаточно высокая.

В целом качество модели признается высоким.

 

Строим график остатков

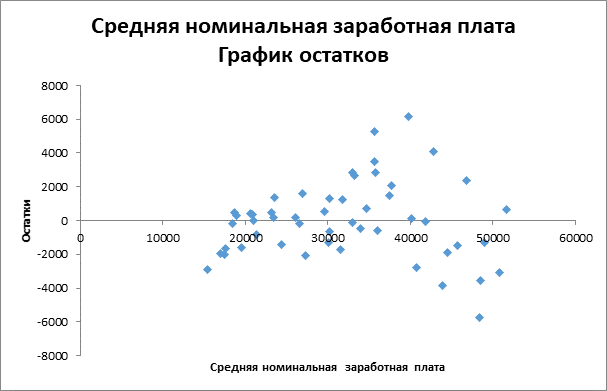
На рис. нет особых различий между ошибками, соответствующими разным значениям Xi. Следовательно, вариации ошибок при разных значениях Хi приблизительно одинаковы

В соответствии с алгоритмом теста Дарбина-Уотсона по оцененной модели вычислим оценки эндогенной переменной

, ,

и остатки

,      ,

по которым по формуле 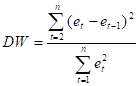  вычислим значение статистики теста. Вычисление показателей удобно выполнять в виде таблицы

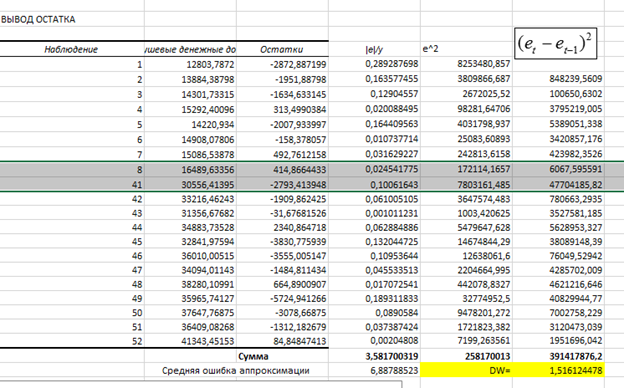
Нижняя и верхняя границы критического значения статистики,  и , определённые по таблице Дарбина-Уотсона для  ,  (число регрессоров модели),  (число наблюдений) делят интервал возможных значений на пять частей

Вычисленное значение статистики попадает в интервал неопределенности. Нельзя сделать вывод на основании данного критерия

 

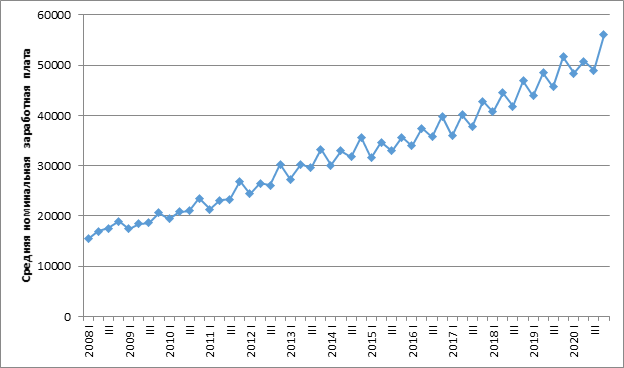
График показывает наличие тренда и сезонной компоненты с периодичностью 4 квартала. Поэтому для учета сезонности понадобится 3 фиктивные переменные.

 

Запишем спецификацию регрессионной модели с фиктивными переменными сдвига, учитывающими сезонные колебания

,      

 ,  .

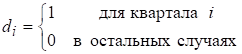Параметры ,  показывают средние квартальные отклонения средней номинальной заработной платы по отношению к четвертому (базовому) кварталу. Построим полученную модель с использованием сервиса Анализ данных – Регрессия

 

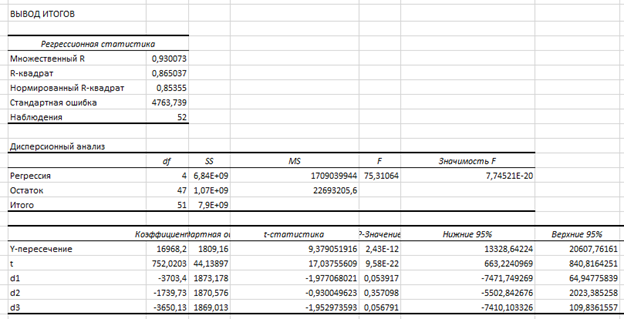 Оцененная модель имеет вид:

, 

 , ,     .

Влияние первых трех кварталов на эндогенную переменную статистически не значимо отличается от влияния на неё базового (четвертого) квартала для уровня значимости  

Поскольку оцененная модель — множественная регрессионная, для неё необходимо вычислить скорректированный коэффициент детерминации по формуле:

 ,

Также он приведен в первой таблице Регрессионного анализа

Критическое значение F – статистики для параметров: ,

 и уровня значимости  равно , таким образом ,  и, следовательно, оцененная регрессия в целом статистически значима.

 

По оцененной модели построим прогноз на ближайший квартал, т.е. на 1 квартал 2021 года:

Подставляем значения

 Получим:

Подставив прогнозные значения  в модель (1), получим точечный прогноз :

Построим интервальную оценку значения эндогенной переменной   на интервале прогнозирования для момента ,

 нижняя граница интервала прогнозирования;

— верхняя граница интервала прогнозирования;

— табличное значение критерия Стьюдента.

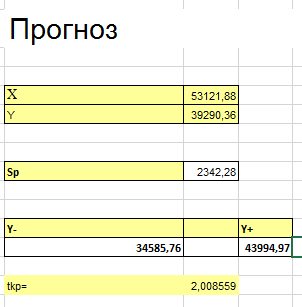
 – ошибка прогноза, вычисляется по формуле:

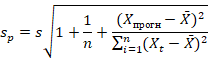
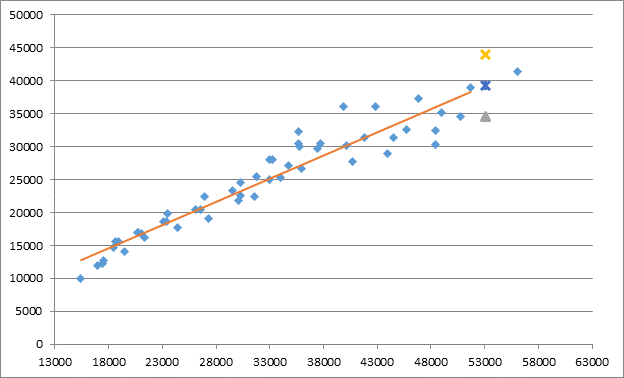
Отразим результаты на графике