Ниже приведен текстовый отчет о решении. Закачка решения в Excel начнется автоматически через 10 секунд. 

 

Введение

В Российской Федерации большое внимание уделяется проблеме общественного здоровья, что связано с неблагоприятной демографической ситуацией в стране: естественной убылью, депопуляцией, постарением населения страны. Смертность населения в трудоспособном возрасте считается одной из наиболее важных медикодемографических и социально-экономических проблем нашего государства.

Этим и обусловлена актуальность выбранной темы

Задачами корреляционно-регрессионного анализа являются обоснование взаимосвязи факторов, влияющих на результативный показатель, а также определение степени влияния каждого фактора на этот показатель.

Для достижения цели необходимо поставить следующие задачи:

·        выявить от каких показателей зависит количество зарегистрированных смертей на 1000 человек населения;

·        определить факторные и результативный признаки для определения корреляционной связи;

·        найти парные коэффициенты корреляции, определить их значимость, проверить на мультиколлинеарность;

·        сделать выводы о степени взаимосвязи между количеством зарегистрированных смертей на 1000 человек населения и каждым фактором в отдельности, а также между количеством зарегистрированных смертей на 1000 человек населения и всеми факторами вместе.

·        выявить основные факторы, которые влияют на количество зарегистрированных смертей на 1000 человек населения;

·        провести отбор факторов и определить методы моделирования;

·        применяя метод пошагового отбора построить модели множественной регрессии и определить наиболее значимую из них;

·        проинтерпретировать результаты для окончательной модели, и определить влияние значимых факторов на результат.

·        проанализировать качество полученной модели и сделать выводы о пригодности для прогнозирования.

Предметом исследования является выявление взаимосвязи между количеством зарегистрированных смертей на 1000 человек населения и другими показателями, а также построение значимой регрессионной модели, пригодной для прогнозирования.

Объект исследования показатели трех федеральных округов РФ – Центрального, Северо-Западного и Южного.

 

 

 

Предварительный анализ данных

Данные взяты по Центральному ФО, Северо-Западному и Южному ФО РФ за 2020 год

Для исследования были выбраны следующие показатели

·        Количество зарегистрированных смертей на 1000 человек населения (результативный признак);

·        Среднедушевые денежные доходы населения, руб.) (факторный признак х₁);

·        Средний размер назначенных пенсий, руб. (факторный признак х₂);

·        Численность врачей на 10 000 человек населения (факторный признак х₃);

·        Число больничных организаций (факторный признак х₄).

Источник: https://rosstat.gov.ru/folder/210/document/12994

Таблица 1 – Исходные данные

 

 

 

2.Расчет коэффициентов корреляции

Построим корреляционную матрицу, используя функцию «Данные»  «Анализ данных»  «Корреляция» табличного процессора MS Excel.

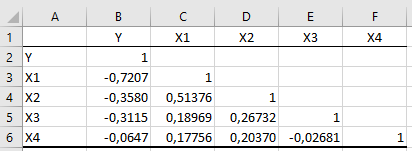
Рис.1.Корреляционная матрица

Проводим анализ коэффициентов корреляции результативного признака с факторными.

– связь прямая и высокая;

 – связь обратная и умеренная;

 – обратная и умеренная;

– связь практически отсутствует.

Из корреляционной матрицы видно, что показателей межфакторной связи между факторами, которые превышают 0,6, нет, следовательно, между признаками мультиколлинеарность отсутствует. Но так как у факторного признака Х₄ с результативным связи практически нет, а с другими факторными признаками есть, то удаляем его из модели.

 

 

Построение эконометрической модели методом пошагового исключения переменных

1.Построим уравнение множественной регрессии с оставшимися тремя факторами с помощью надстройки «Анализ данных» ППП MS Excel. Результаты приведены в Приложении 1.

Уравнение множественной регрессии с факторами Х₁, Х₃, Х₄ имеет вид:

Проанализируем показатели качества данной модели.

Из протокола регрессионного анализа получены значения коэффициента множественной корреляции и коэффициента детерминации.

Коэффициент корреляции – . Следовательно, связь результативного – признака количество зарегистрированных смертей с факторными высокая

Коэффициент детерминации . Следовательно, 55,37% вариации количества зарегистрированных смертей объясняется вариацией изменения факторов Х₁, Х₂, Х₃, остальные 44,63% вариацией других признаков, не включенных в модель.

Проверим адекватность модели при заданном уровне значимости.

Значимость уравнения проверим с помощью критерия Фишера: .Табличное значение при уровне значимости 5% и степенях свободы ;  равно:

Так как наблюдаемое значение критерия Фишера больше табличного, уравнение признается значимым.

Проверим значимость коэффициентов уравнения при заданном уровне значимости.

Для начала вычислим табличное значение t-статистики при уровне значимости 5% и количестве степеней свободы 30: .

Находим t-статистики для параметров уравнения. Параметр признается значимым, если значение его t-статистики больше табличного. Анализ параметров приведен в таблице 2.

Уравнение содержит незначимые параметры. Наименьшая t-статистика у коэффициента , следовательно, переменную Х₃ следует удалить из модели. В дальнейшем такое удаление необходимо проводить до тех пор, пока в модели не останутся только значимые параметры.

 

Таблица 2 –  Анализ значимости параметров уравнения регрессии с тремя факторами

 

2.Построим уравнение множественной регрессии с двумя факторами. Результаты приведены в Приложении 2.

Из таблицы видно, что уравнение множественной регрессии с пятью факторами имеет вид:

Проанализируем показатели качества данной модели.

Из протокола регрессионного анализа получены значения коэффициента множественной корреляции и коэффициента детерминации.

Коэффициент корреляции – . Следовательно, связь результативного – признака количество зарегистрированных смертей с факторными высокая

Коэффициент детерминации . Следовательно, 55,11% вариации количества зарегистрированных смертей объясняется вариацией изменения факторов Х₁, Х_3, остальные 44,89% вариацией других признаков, не включенных в модель.

Проверим адекватность модели при заданном уровне значимости.

Значимость уравнения проверим с помощью критерия Фишера:

Табличное значение при уровне значимости 5% и степенях свободы ; равно:

Так как наблюдаемое значение критерия Фишера больше табличного, уравнение признается значимым.

Проверим значимость коэффициентов уравнения при заданном уровне значимости.

Для начала вычислим табличное значение t-статистики при уровне значимости 5% и количестве степеней свободы 31: .

Находим t-статистики для параметров уравнения. Параметр признается значимым, если значение его t-статистики больше табличного. Анализ параметров приведен в таблице 3.

Таблица 3 – Анализ значимости параметров уравнения регрессии с двумя факторами

 

Уравнение содержит один незначимый параметр. Его t-статистика у коэффициента , следовательно, переменную Х₃ следует удалить из модели.

Построим уравнение парной регрессии . Результаты приведены в Приложении 3.

 

 

Уравнение парной регрессии имеет вид:

Проанализируем показатели качества данной модели.

Из протокола регрессионного анализа получены значения коэффициента корреляции и коэффициента детерминации.

Коэффициент корреляции – . Следовательно, связь результативного – признака (количество зарегистрированных смертей) с факторным (число больничных организаций) высокая

Коэффициент детерминации . Следовательно, 51,94% вариации количества зарегистрированных смертей объясняется вариацией изменения фактора Х₁, остальные 48,06% вариацией других признаков, не включенных в модель.

Проверим адекватность модели при заданном уровне значимости.

Значимость уравнения проверим с помощью критерия Фишера: .Табличное значение при уровне значимости 5% и степенях свободы ; равно:

Так как наблюдаемое значение критерия Фишера больше табличного, уравнение признается значимым.

Проверим значимость коэффициентов уравнения при заданном уровне значимости.

Для начала вычислим табличное значение t-статистики при уровне значимости 5% и количестве степеней свободы 31: .

Находим t-статистики для параметров уравнения. Параметр признается значимым, если значение его t-статистики больше табличного. Анализ параметров приведен в таблице 4.

 

 

Таблица 4 – Анализ значимости параметров уравнения парной регрессии

 

Уравнение не содержит незначимых параметров. Среднедушевые денежные доходы значимо влияют на количество зарегистрированных смертей.

Таким образом окончательная регрессионная модель имеет вид:

Экономическая интерпретация: при увеличении среднедушевых доходов населения на 10000 руб. количество зарегистрированных смертей снизилось на 1,77 случаев на 1000 человек

Проверим качество модели с помощью средней ошибки аппроксимации. Строим вспомогательную таблицу (таблица 5).

Таблица 5 – Вспомогательные расчеты для определения средней ошибки аппроксимации

 

Средняя ошибка аппроксимация будет:

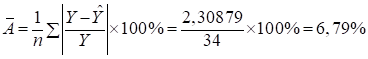
Значение данного показателя не превышает 7%, следовательно, качество модели хорошее, и его можно использовать для прогнозирования.

 

 

Заключение

В процессе данного исследования был проведен корреляционно-регрессионный анализ показателей трех субъектов РФ (Центральный, Северо-Западный и Южный ФО), влияющих на смертность населения. Целью такого анализа было выявление взаимосвязи между показателями и выбор факторов для построения адекватной регрессионной модели.

Для исследования были выбраны данные Росстата (ссылка ttps://rosstat.gov.ru/folder/210/document/12994).

Первоначально была оценена и взаимосвязь между показателями. С этой целью была построена корреляционная матрица. Между факторами мультиколлинеарность обнаружена не была. Однако, встал вопрос об исключении одной переменной из модели, так как между ней и результативным фактором отсутствовала связь.

В дальней в процессе реализации метода пошагового исключения переменных пришлось удалить еще несколько признаков.

В результате применения данного метода оказалось, что значимо влияет на результат только 1 фактор – среднедушевые доходы населения. Между ними и смертностью обратная связь – при увеличении среднедушевых доходов населения на 10000 руб. количество зарегистрированных смертей снизилось на 1,77 случаев на 1000 человек.

Окончательное уравнение парной регрессии Y(X₁) имеет вид:

 

 

Список литературы

1.     Айвазян, С. А. Эконометрика / С.А. Айвазян, С.С. Иванова. – М.: Маркет ДС, 2017. – 104 c.

2.     Андрианов В. Инфляция: основные виды и методы регулирования // Экономист. – 2015. – № 6. – С. 18–22.

3.     Атамазова А.А., Баташева Э.А. Современная безработица в России в условиях нестабильности // Молодой ученый. – 2016. – №1. – С. 298–300.

4.     Артамонов, Н. В. Введение в эконометрику / Н.В. Артамонов. – М.: МЦНМО, 2016. – 224 c.

5.     Афанасьев, В. Н. Эконометрика / В.Н. Афанасьев, М.М. Юзбашев, Т.И. Гуляева. – М.: Финансы и статистика, 2017. – 256 c.

6.     Вербик, Марно Путеводитель по современной эконометрике / Марно Вербик. – М.: Научная книга, 2016. – 616 c.

7.     Герасимов, Е.И. Громов. – М.: Феникс, 2016. – 336 c.

8.     Колемаев, В. А. Эконометрика / В.А. Колемаев. – М.: ИНФРА–М, 2016. – 160 c.

9.     Математика для экономистов. От Арифметики до Эконометрики / Н.Ш. Кремер и др. – М.: Юрайт, 2017. – 688 c.

10. Теория статистики с элементами эконометрики. Учебник. – М.: Юрайт, 2015. – 672 c.

11. Тихомиров, Н. Методы эконометрики и многомерного статистического анализа / Н. Тихомиров. – М.: Экономика, 2017. – 989 c.

12. Эконометрика / Под редакцией В.Б. Уткина. – М.: Дашков и Ко, 2017. – 562 c.

13. Яновский, Л. П. Введение в эконометрику / Л.П. Яновский, А.Г. Буховец. – М.: КноРус, 2017. – 256 c.

 

Приложение

Приложение 1

Протокол регрессионного анализа модели с переменными Х₁, Х₂, Х₃.

Регрессионная статистика
Множественный R	0,74412561
R-квадрат	0,55372293
Нормированный R-квадрат	0,50909522
Стандартная ошибка	1,35343401
Наблюдения	34
Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия	3	68,18413818	22,72804606	12,4076041	1,89E-05
Остаток	30	54,95350887	1,831783629
Итого	33	123,1376471
	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%
Y-пересечение	22,7735185	1,761133768	12,93116906	8,4315E-14	19,1768
X1	-0,00017614	3,50636E-05	-5,023366912	2,1809E-05	-0,00025
X2	3,2056E-05	7,63533E-05	0,419836636	0,67759641	-0,00012
X3	-0,05517964	0,036438485	-1,514323241	0,14040962	-0,1296

 

 

 

Приложение 2

Протокол регрессионного анализа модели с переменными Х₁, Х₃.

Регрессионная статистика
Множественный R	0,742361676
R-квадрат	0,551100857
Нормированный R-квадрат	0,522139622
Стандартная ошибка	1,335331108
Наблюдения	34
Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия	2	67,86126	33,93063	19,0289142	4,06E-06
Остаток	31	55,27638	1,783109
Итого	33	123,1376
	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%
Y-пересечение	22,91585966	1,705076	13,43979	1,7974E-14	19,43834
X1	-0,000168932	3,02E-05	-5,59972	3,8479E-06	-0,00023
X3	-0,05209461	0,035213	-1,47943	0,14911537	-0,12391

 

 

 

Приложение 3

Протокол регрессионного анализа модели парной регрессии с переменной Х₁

Регрессионная статистика
Множественный R	0,720698781
R-квадрат	0,519406733
Нормированный R-квадрат	0,504388194
Стандартная ошибка	1,359907213
Наблюдения	34
Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия	1	63,95852	63,95852	34,58437	1,53E-06
Остаток	32	59,17912	1,849348
Итого	33	123,1376
	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%
Y-пересечение	20,80873062	0,954648	21,79729	9,12E-21	18,86418
X1	-0,000177398	3,02E-05	-5,88085	1,53E-06	-0,00024