Анализ панельных данных в Eviews

Ниже приведены условия задач, и текстовый отчет о решении. Закачка полного решения(документы  doc и wf1 в архиве rar) начнется автоматически через 10 секунд. 

Анализ панельных данных

1. Данные

Рассмотрим работу, связанную с моделирование влияния показателей Европейских банков на величину системного риска в банковском секторе, данные за период 2010-2020 из статистических отчетов банков.

Итого в выборке 15 банков (кросс-секций) за 40 периодов (четыре квартала с 2010 по 2020 гг.)

В анализе участвуют отчеты следующих банков:

·        Natwest Group

·        BNP Paribas

·        Deutsche Bank

·        Credit Agricole

·        Barclays

·        ING Groep

·        Commerzbank

·        Lloyds

·        Societe General

·        UBS

·        Santander

·        HSBC

·        Credit Suisse

·        BBVA

·        UniCredit

Для каждого банка были отобраны следующие факторы:

·        Vol (волатильность рыночной капитализации банка)

·        Lev (левередж, заемные средства по отношению к капиталу банка)

·        NPL (non performing loans:отношение рисковых кредитов ко всем кредитам) Tier1 (адекватность капитала банка, можно сказать резервный капитал на возможные потери, рассчитывается относительно рисковых активов)

·        SIZE (совокупные активы банков)

 

2.Анализ в EViews

2.1 Предварительный анализ

Цель – подобрать вид модели (спецификация)

Необходимым этапом определения спецификации панельных моделей является графический анализ исходных данных. Для построения графиков различного вида необходимо открыть ряд данных панельной структуры и выбрать в меню View команду Graph… (рисунок 2.6). Далее появится окно GraphOptions(рисунок 2.7), позволяющее как задать тип графика (Graphtype), так и  определить специфику построения именно графиков для данных панельной структуры (PanelOptions).

Рисунок 2.6. Выбор режима построения графиков

Рисунок 2.7. Окно задания параметров для построения графиков

Для просмотра графика, на котором представлено множество временных рядов для каждого индивидуального наблюдения (кросс-секции) следует в поле PanelOptions выбрать команду Combinedcrosssections, и появится соответствующий график (рисунок 2.8).

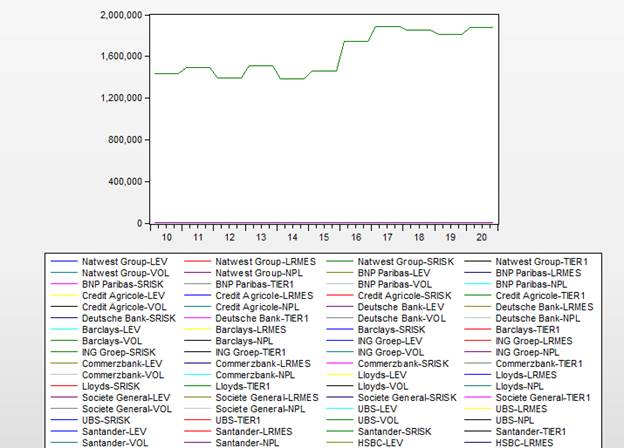
Рисунок 2.8.  Обобщенный график временных рядов Srisk для всех кросс-секций

Для построения общего графика, как среднего значения по всем кросс-секциям для каждого временного периода (рисунок 2.9), необходимо выбрать команду MeanplusSDboundsв меню Panel Options.

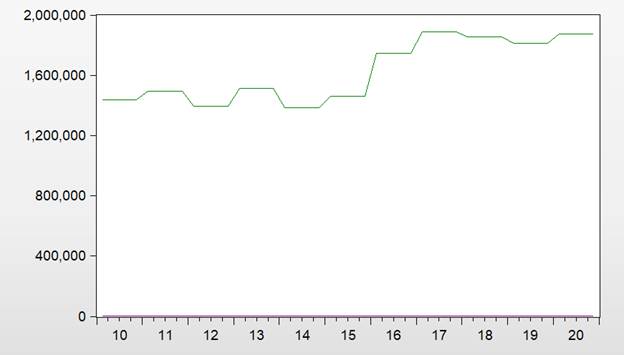
Рисунок 2.9. График среднего значения по всем кросс-секциям для каждого временного периода

Видим, что системный риск после 2015 года резко возрос.

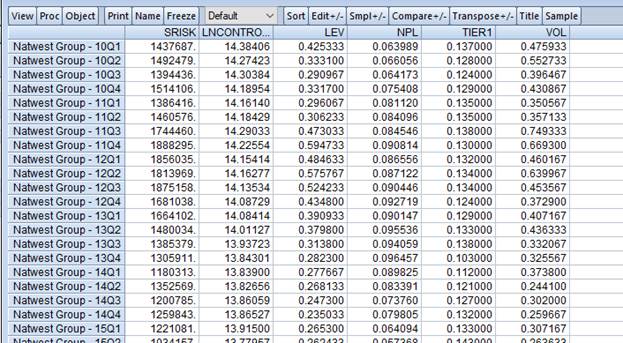
Рисунок 2.10. Данные по всем кросс-секциям для каждого временного периода

 

Для построения индивидуальных графиков временных рядов для каждой из кросс-секций следует выбрать команду Individualcrosssectionsв меню PanelOptions.

Для просмотра описательных обобщенных статистик панельных переменных следует открыть ее и выбрать в меню View команду DescriptiveStatistics&Tests, далее Stats Table (рисунок 2.11).

Рисунок 2.11. Просмотр описательных обобщенных статистик панельных переменных

На рисунке 2.12 показаны результаты обобщенных панельных статистик, рассчитанных как средние значения по всем кросс-секциям и периодам: Mean– среднее значение, Median– медиана, Std. Dev. – стандартное отклонение; Skewness– коэффициент асимметрии, Kurtosis – коэффициент эксцесса, Jarque-Bera– статистика Жарка-Бера и соответствующий ей уровень значимости Probabilityдля отклонения гипотезы о соответствии переменной нормальному распределению.

Для отображения описательных статистик для элементов панельного ряда данных, классифицированных по категориям другого панельного ряда следует выбрать в меню View команду DescriptiveStatistics & Tests, далее Stats by Classification… (рисунок2.11), появится диалоговое окно Statistics By Classification… (рисунок 2.13).

Рисунок 2.12. Обобщенные описательные статистики панельных переменных

Из таблицы видно, что

Среднее значение системного риска равно 1 308 260

Среднее значение логарифма совокупных активов банков равно 13,969

Среднее значение леверджа в процентном отношении равно 0,372%.

Среднее процентное значение рисковых кредитов равно 0,43%

Среднее процентное значение резервного капитала равно 0,1418%

Среднее процентное значение рыночной волатильности капитализации равно 0,3755%

Рисунок 2.13. Задание классификации для описательных статистик

Результаты расчета описательных статистик для элементов панельного ряда данных, классифицированных по категориям другого панельного ряда представлены в таблице на рисунке 2.14.

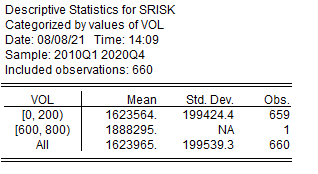
Рисунок 2.14. Описательные статистики для элементов панельного ряда данных, классифицированных по категориям другого панельного ряда

 

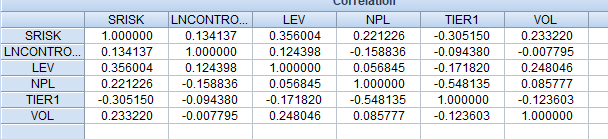
Рисунок 2.15. Корреляционная матрица для элементов панельного ряда данных.

Из данных таблицы можно заключить, что:

Самый большой коэффициент корреляции с SRISK у фактора LEV

Связь положительная, средняя.

Связь отрицательная, средняя.

Самое небольшое значение

 

2.2 Тестирование данных на панельные единичные корни

Для определения структуры панельных рядов (типов процессов) необходимо проводить панельные тесты на единичные корни. Для предварительного анализа структуры панельных переменных может быть полезен анализ коррелограмм автокорреляционной и частной автокорреляционной функций панельных переменных. Для их построения следует открыть панельную переменную и выбрать меню View, далее команда Correlogram… (рисунок 2.17).

Рисунок 2.17. Выбор меню для построения коррелограмм

Построить коррелограммы можно как для исходного ряда Level, так и для первых 1^stdifferenceи вторых разностей 2^nddifference соответственно. При этом выбирается длина лага запаздывания Lagstoincludeдля отражения коррелограмм (рисунок 2.18).

Рисунок 2.18.Окно спецификации коррелограмм

На рисунке 2.19 представлены коррелограммы автокорреляционной (Autocorrelation) и частной автокорреляционной (PartialCorrelation) функций панельных переменных.

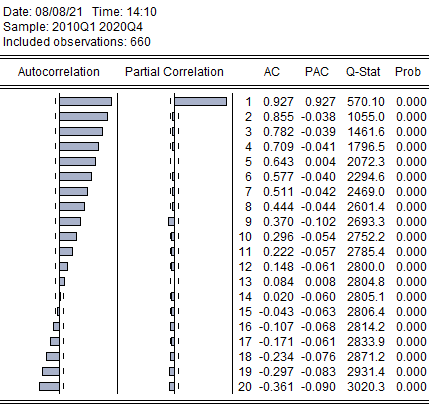
Рисунок 2.19. Коррелограммы панельной переменной Srisk

 

 Для проведения тестов на панельные единичные корни необходимо в меню View открытой переменной выбрать  команду UnitRootTest (рис. 2.20), далее в появившемся окне PanelUnitRootTest в поле Testtype выбрать требуемый тест на единичные корни ( рис. 2.21):

-     Обобщенный тест (Summary)

-     Тест на обобщенные единичные корни Левина-Лина-Чу (Commonroot – Levin, Lin, Chu);

-     Тест на обобщенные единичные корни Брейтунга (Commonroot – Breitung);

-     Тест на индивидуальные единичные корни Има-Песрана-Шина (Individualroot – Im, Pesaran, Shin);

-     Тест на индивидуальные единичные корни Фишера - расширенный Дики-Фуллера (Individualroot – Fisher- ADF);

-     Тест на индивидуальные единичные корни Фишера – Филипса-Перрона (Individualroot – Fisher- РР);

-     Тест Хадри (рис. 2.22) Hadri.

Для определения типа процесса рекомендуется пользоваться несколькими тестами

Рисунок 2.20. Переход к проведению процедуры определения панельных единичных корней

Рисунок 2.21. Выбор теста панельных единичных корней

 

 

Рисунок 2.22. Настройки теста Хадри

Результаты теста Хадри представлены на рисунке 2.23. Для теста рассчитывается Z-статистика (HadriZ-stat), и соответствующей ей уровень значимости Prob., отказа от нулевой гипотезы, о том, что панельный процесс является стационарным. Наряду с обычной статистикой Хадри оценивается статистика с учетом возможной гетероскедастичности (HeteroscedasticConsistentZ-stat), выполненная в оценках Невье-Уеста.

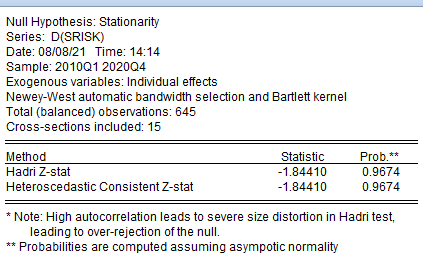
Рисунок 2.23. Результаты теста Хадри

Для обобщенного теста (Summary) результаты вывода представлены на рисунке ниже:

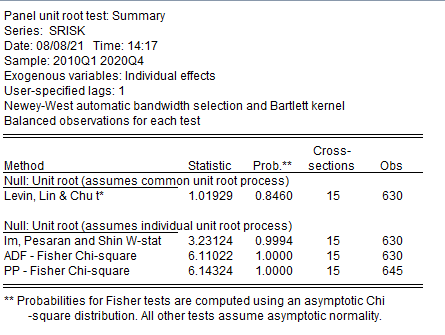
Единичные корни есть, ряд не стационарный.

 

В результате можно сделать вывод о том, что панельный процесс является не стационарным на уровнях ряда, целесообразна спецификация модели первой разности ряда.

Проведем тест для первых разностей

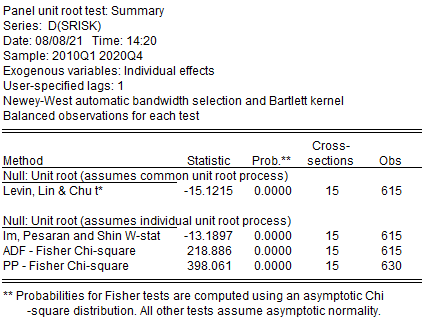
Для вторых разностей

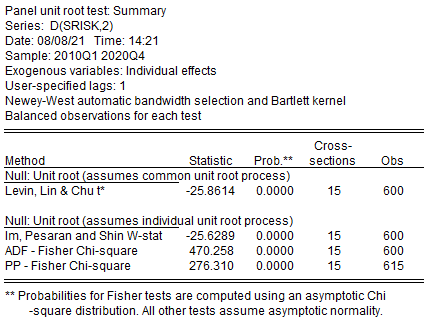
Единичных корней нет, ряды стационарные.

Переменная стационарна по всем тестам только для первых и вторых разностей.

Можно проверять коинтеграцию рядов.

2.3 Проверка коинтеграции панельных переменных

Для проведения теста на коинтеграцию откроем панельные переменные, участвующие в коинтеграционном соотношении, как группу.

В данном тесте можно задать различную панельную спецификацию тестируемой модели в поле Deterministictrendspecification (рисунок 2.28):

1) при наличии индивидуальных констант в коинтеграционном соотношении ;

2) при наличии индивидуальных констант и индивидуального тренда для каждого наблюдения;

3) отсутствие индивидуальных констант и индивидуального тренда .

Рисунок 2.25. Открытие переменных как группы

 

Рисунок 2.26. Проведение теста на панельную коинтеграцию

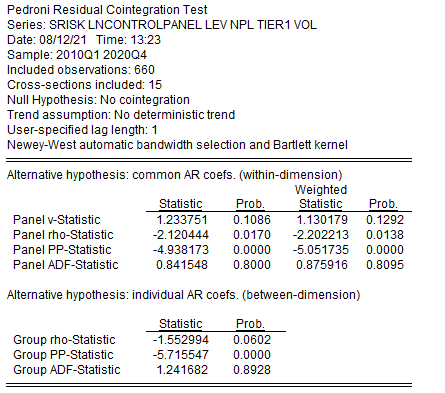
Результаты теста Педрони представлены на рисунке ниже, как видно здесь нулевая гипотеза об отсутствии панельной коинтеграции проверяется с двумя возможными альтернативными гипотезами:

1)     Наличие обобщенных коэффициентов авторегрессии, что соответствует Within-оценкам:

Рассчитываются статистика Вальда (Panelv-Statistic), ρ-статистика (Panelrho-Statistic), статистика Филипса-Перрона (PanelPP-Statistic), статистика расширенного теста Дики-Фуллера (PanelADF-Statistic) для проверки нулевой гипотезы.

2)    Наличие индивидуальных коэффициентов авторегрессии, что соответствует Between-оценкам:

Рассчитываются ρ-статистика (Grouprho-Statistic), статистика Филипса-Перрона (Group РР-Statistic), статистика расширенного теста Дики-Фуллера (Group ADF -Statistic) для проверки нулевой гипотезы.

Рисунок 2.27. Настройка теста на панельную коинтеграцию Педрони

(а)

(б)

Рисунок 2.28. Результаты теста Педрони (с индивидуальной константой – а, без индивидуальной константы - б)

Можно сделать вывод о том, что коинтеграция на уровне  ряда при отсутствии индивидуальных констант в коинтеграционном соотношении подтверждается.

 

Для выполнения теста на причинность следует в открытой группе переменных зайти в меню View и выбрать GrangerCausality(рисунок 2.30).

Рисунок 2.30. Выбор команды для проведения тестов на панельную причинность

В появившемся диалоговом окне (рисунок 2.31) следует указать длину максимального лага запаздывания, для учета в модели  авторегрессии с распределенными лагами в уравнениях:

, или

.

Рисунок 2.31. Спецификация, задающая максимальный лаг запаздывания в тесте панельную на причинность по Грэнждеру

Результаты проведения теста на причинность по Гренждеру представлены на рисунке 2.32. Проверяются две нулевые гипотезы с помощью теста Фишера (F-statistic) о том, что одна из переменных не является причиной другой, и наоборот, что другая переменная не является причиной первой.

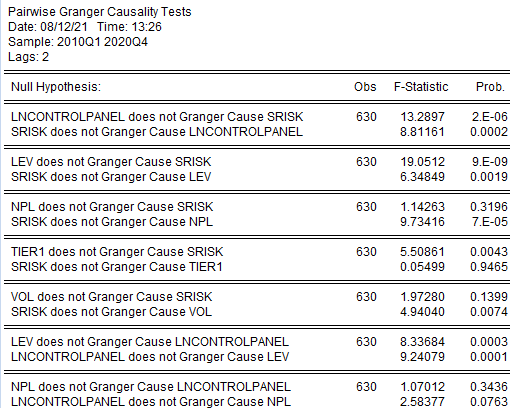
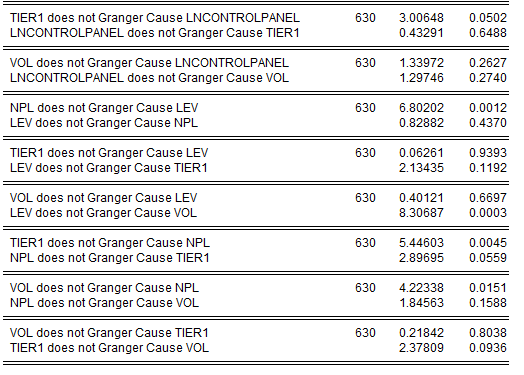
Рисунок 2.32. Результаты теста на панельную причинность по Гренджеру

Нулевая гипотеза о том, что TIER1, LEV, VOL не является причиной по Гренджеру для SRISK отклоняется на очень малой вероятности, следовательно, она такой причиной является, как мы и предполагали.

 

Для определения максимального лага запаздывания для моделей  авторегрессии с распределенными лагами, служащими основой для проведения теста на причинность, можно проанализировать кросскоррелогаммы. Для их построения необходимо в меню View выбрать команду CrossCorrelation(рисунок 2.30). Максимальный лаг запаздывания равен  наибольшему лагу, при котором коэффициенты кросс корелляционных функций статистически значимы, то есть выходят за границу зоны незначимости, отмечаемой на графиках пунктирной линией (рисунок 2.33).

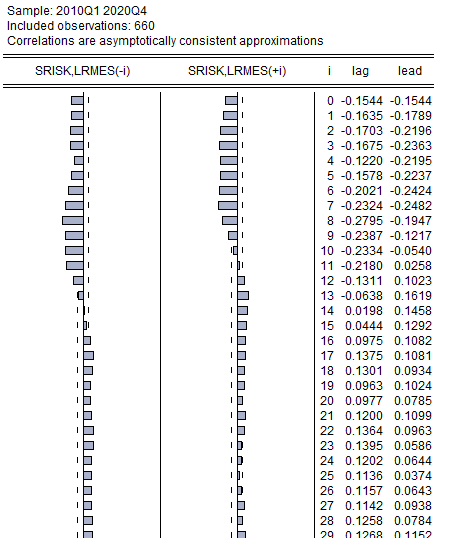
Рисунок 2.33. Кросс-коррелограммы панельных переменных  SRISK и LRMES

В данном случае, что максимальный лаг запаздывания составляет 10 кварталов.

2.4Оценивание панельных моделей

Для оценки панельной модели необходимо в рабочем файле (Workfile) выбрать необходимые переменные (сначала зависимую, а затем регрессоры), и нажав правую кнопку мыши, в появившемся меню выбрать последовательно команды OpenasEquation (рисунок 2.34).

Рисунок 2.34. Построение панельных моделей

Появится диалоговое окно задания спецификации панельных моделей (рисунок  2.35), в центре которого в поле EquationSpecification отражено поле спецификации модели. Для проведения оценки методом наименьших квадратов в списке Method следует выбрать панельный метод наименьших квадратов LS.

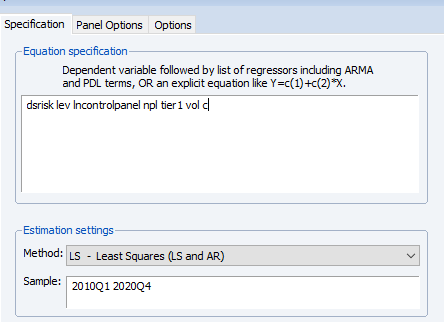
Рисунок 2.35. Окно задания спецификации панельных моделей

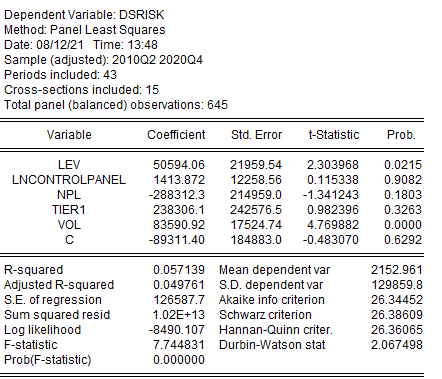
Рисунок 2.36. Вывод итогов панельной модели

Данная модель имеет не значимый коэффициент детерминации

Для задания спецификации панельных эффектов следует в окне задания спецификации панельной модели зайти во вкладку PanelOptions. Здесь можно выбрать в поле Effects specificationспецификации для включения фиксированных эффектов (Fixed), случайных эффектов (Random) и невключения эффектов (None) как для объектов наблюдения (Cross-section) так и по периодам (Period), см. рисунок 2.36.

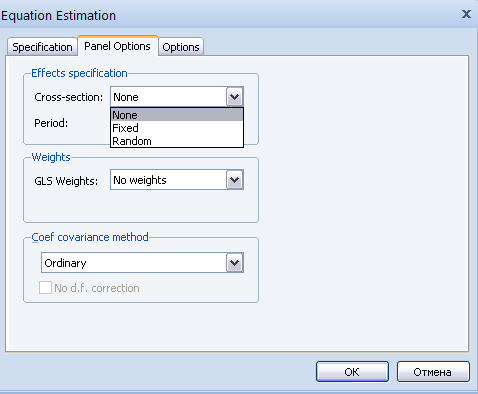
Рисунок 2.36. Окно вкладки задания спецификации панельных эффектов

Оценим модель с фиксированными индивидуальными эффектами. Результаты оценки представлены на рисунке 2.37.

В информационной части окна указана зависимая переменная (DependentVariable), метод оценивания модели (Method), количество включенных периодов панели (Periodincluded), количество включенных кросс-секций (Cross-sectionincluded), общее количество наблюдений в панели (Totalpanelobservations). Далее в таблице указаны результаты оценивания, где в столбце Variable указаны регрессоры и свободный член С, в столбце Coefficient соответствующие им оценки коэффициентов модели, в столбце Std. Error стандартные ошибки коэффициентов, в столбцах t-Statistic и Prob. t-статистики и соответствующие им уровень значимости.

Далее указаны параметры спецификации панельной модели EffectsSpecification: наличие фиксированных (Fixed) или случайных эффектов (Random). В случае построения обобщенной панельной модели, в которой отсутствуют индивидуальные константы, данного поля в окне результатов не будет. Далее под таблицей указаны основные показатели и критерии качества построенной панельной модели. Следует отметить, что в Eviews существует возможность сохранить уравнение в виде объекта, для этого следует в окне результатов выбрать менюName, и в появившемся окне задать имя для уравнения. В результате в рабочем файле появится новый объект .

Для проверки нулевой гипотезы о незначимости панельной модели в целом, то есть одновременном равенстве всех коэффициентов модели нулю) используют критерий Фишера: F- статистика  и соответствующий ей уровень значимости , также представлены в окне результатов (рисунок 2.37).

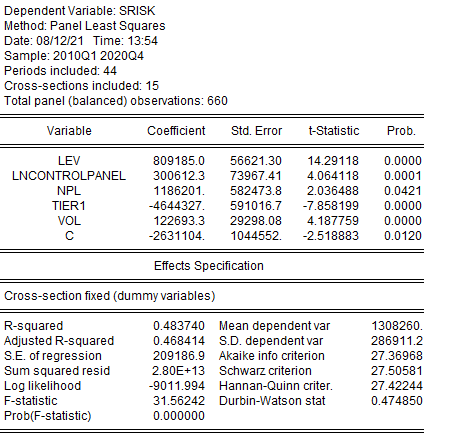
Рисунок 2.37. Результаты оценки модели панельным МНК с фиксированными эффектами.

В нашем случае, уровень значимости равен 0, а значит модель с фиксированными индивидуальными эффектами в целом значима.

Перестроим модель как обобщенную, без индивидуальных эффектов.

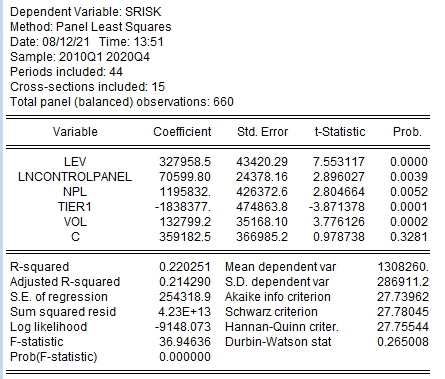
Рисунок 2.38. Результаты оценки модели панельным МНК без эффектов.

 

Модель в целом стала значимой, т.к. F-статистика составляет 0.0.

Для проведения теста на выбор между обобщенной моделью и моделью с фиксированными эффектами также следует в окне результатов оценки модели с фиксированными эффектами войти в меню View, выбрать команду Fixed/RandomEffectsTesting, далее RedundantFixedEffects – LikelihoodRatio (тест отношения правдоподобия), рисунок 2.38.

 

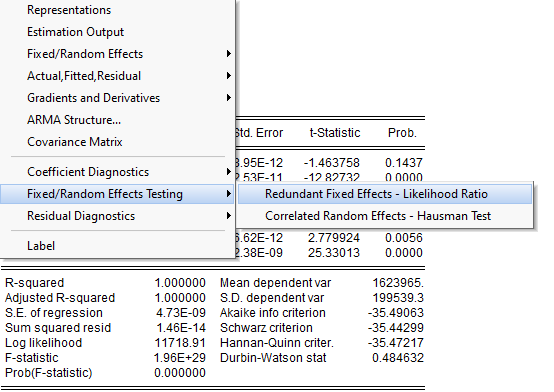
Рисунок 2.38. Задание тестов на спецификацию панельных эффектов

На рисунке 2.39 представлен результат проведения теста  на выбор между обобщенной моделью и моделью с фиксированными эффектами для наблюдений. В таблице даны значения статистики (столбец Statistic) Фишера (F) и в столбце Prob. соответствующей уровень значимости для нулевой гипотезы об отсутствии в модели фиксированных панельных эффектов.

 

 

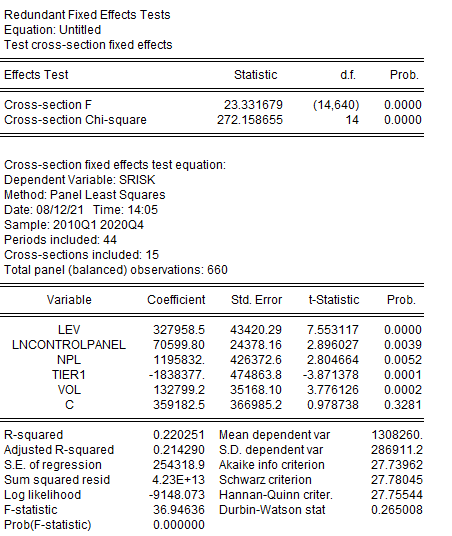
Рисунок 2.39. Результат теста на спецификацию панельных эффектов (между обобщенной моделью и моделью с фиксированными эффектами)

Видим, что гипотеза отвергается, следовательно, есть основание учитывать индивидуальные фиксированные эффекты в модели.

Теперь оценим модель со случайными эффектами.

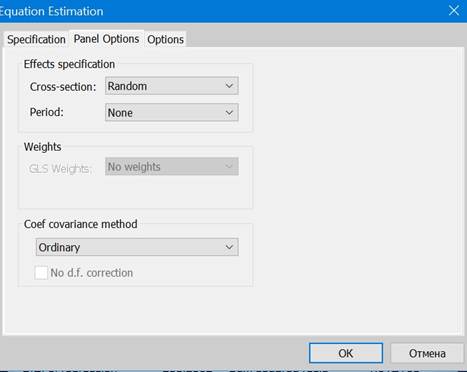
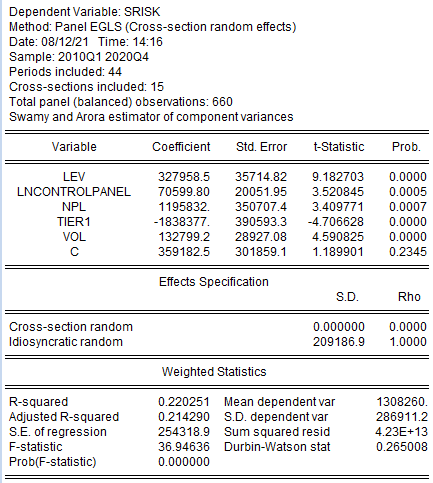
Рисунок 2.40. Модель со случайными эффектами

 

Модель со случайными эффектами значима.

Для проведения теста на выбор между моделью с фиксированными эффектами и моделью со случайными эффектами следует в окне результатов модели со случайными эффектами войти в меню View, выбрать команду Fixed/Random Effects Testing, далее Correlated Random Effects – Hausman Test (тестХаусмана), рисунок2.38.

Результат проведения теста на выбор между моделью с фиксированными эффектами и моделью со случайными эффектами представлен на рисунке 2.40. В таблице дана в столбце Chi-Sq. Statistic статистика Хаусмана, удовлетворяющая χ²-распределению, соответствующий ей уровень значимости для нулевой гипотезы об отсутствии случайных эффектов в модели, дан в столбце Prob.

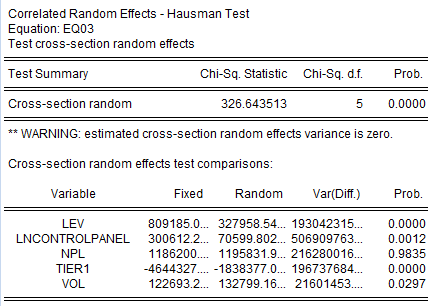
Рисунок 2.40. Результат теста Хаусмана на спецификацию панельных эффектов

Поскольку p-value составляет 0,0 то гипотезу об отсутствии случайных эффектов в модели отвергаем. Есть основания предполагать, что по кросс-секциям наилучшей является модель c фиксированными эффектами.

Для проведения мониторинга модели проверяются показатели качества оценки модели, в частности показатель панельный коэффициент детерминации R², показывающий долю объясненной уравнением дисперсии:

R²=0,4837

Также можно рассматривать как показатель качества скорректированный на число степеней свободы панельный коэффициент детерминации на рисунке 2.37:

Adjusted R²=0,468

Для проверки гипотезы об отсутствии автокорреляции в остатках панельной модели анализируется статистика Дарбина-Уотсона.

 

Для оценки нормальности распределения остатков панельной модели можно проанализировать гистограмму распределения и результаты теста Бера-Жарка. Для этого необходимо в окне результатов моделирования выбрать меню View, ResidualDiagnostics, далее Histogram – NormalityTest (рисунок 2.41).

Все коэффициентах модели статистически значимы при уровне значимости 5%.

На рисунке 2.42 представлена гистограмма распределения и результаты теста Бера-Жарка.

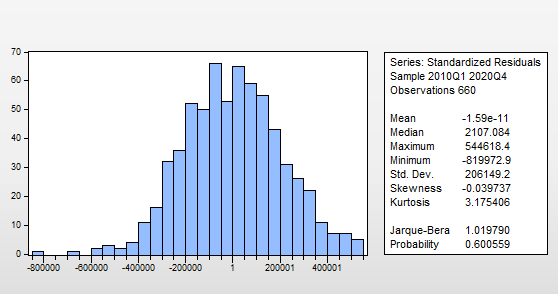
Рисунок 2.42. Гистограмма распределения

Нулевая гипотеза о соответствии распределения нормальному проверяется на основе статистики Жарка-Бера (Jarque-Bera) с указанием соответствующего уровня значимости (Probability). В данном случае, поскольку p-value равно нулю, нулевая гипотеза отклоняется.

Для процедуры проведения селекции панельных моделей анализируется информационные критерии Акайке, Шварца и Ханена-Квина:

 

 

Schwarz criterion	27.50581
Hannan-Quinn criter.	27.42244
Durbin-Watson stat	0.474850

        

Построение панельных моделей с индивидуальными эффектами ПО ПЕРИОДАМ (фиксированные, случайные) не целесообразно.

Лучшей моделью является модель с фиксированными эффектами

Сама модель статистически значима в целом. Коэффициенты модели статистически значимы при уровне значимости 1%. Коэффициент детерминации равен 0,4837

Для оценки качества «подгонки» модели под реальные данные можно просмотреть совместные графики фактических и расчетных значений, а также проанализировать график остатков. Для этого в окне результатов оценки модели в меню View выбрать команду Actual, Fitted, Residual, далее Actual, Fitted, ResidualGraph (рисунок 2.46).

Рисунок 2.46. Построение графика фактических и расчетных значений, а также графика остатков

На рисунке 2.47 представлен график фактических (Actual) и расчетных значений (Fitted), а также график остатков (Residual).

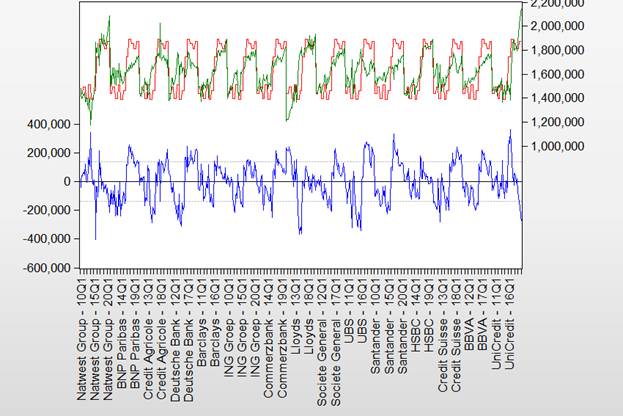
Рисунок 2.47. График фактических и расчетных значений и остатков

 

2.6.Методы оценки панельных моделей при автокорреляции остатков

Для перестройки модели необходимо в окне результатов оценки выбрать меню Proc, далее команду  Specify/Estimate (рисунок 2.48).

Рисунок 2.48. Перестройка панельной модели

В Ewiews имеются возможности получить эффективные оценки модели, несмотря на наличие гетероскедастичности и автокорреляции в остатках панельной модели. Для этого следует для оценки параметров модели применить взвешенные методы наименьших квадратов, где весы подбираются в зависимости от эффектов модели (по кросс-секционным эффектам, либо по эффектам периодов). Для этого в окне оценки модели EquationEstimation во вкладке PanelOptions в поле Weights следует выбрать методы Cross-sectionweights или Periodweights (рисунок 2.49). Выполнить подобные процедуры можно только при наличии соответствующей спецификации у панельной модели. Существуют также методы избавления от автокорреляции в остатках, и как следствие, получения надежных оценок, при использовании  обобщенных методов SUR:  Cross-sectionSUR и PeriodSUR.

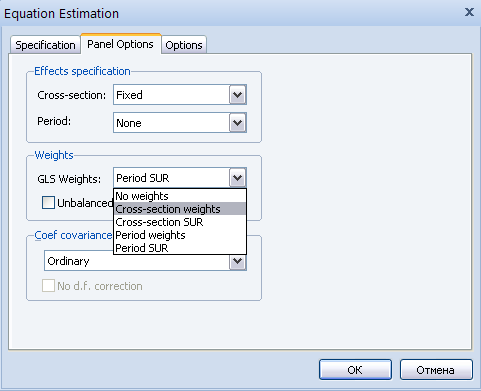
Рисунок 2.49.Спецификация панельного метода оценки модели

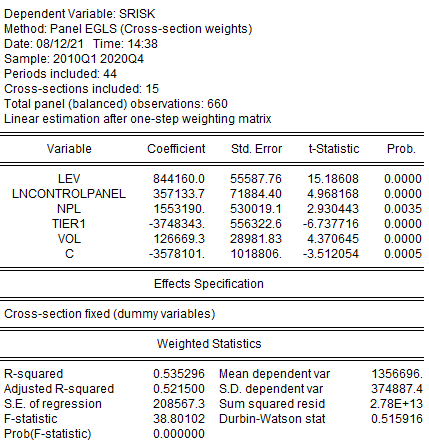
Все коэффициенты модели значимы с уровнем значимости 1%. Модель в целом статистически значима. Коэффициент детерминации .

После построения модели в результатах оценки (рисунок 2.50) будут даны взвешенные оценки коэффициентов модели, полученные взвешенным панельным методом наименьших квадратов,  и указаны соответствующие взвешенные статистики (WeightedStatistics). На рисунке 2.50 представлены результаты оценки модели взвешенным панельным методом наименьших квадратов, с весами подобранными под эффекты по периодам.

Это позволяет устранить автокорреляцию так, что  статистика Дарбина-Уотсона (Durbin-WatsonStat) после «взвешивания» модели  (WeightedStatistics) станет гораздо ближе к 1, что указывает на отсутствие автокорреляции в остатках, и как следствие получение эффективных оценок модели.

2.7.  Прогнозирование по панельной модели

Для построения прогноза по панельной модели следует в окне результатов оценки модели выбрать в меню Proc команду Forecast…(рисунок 2.51).

Рисунок 2.51. Выбор меню для построения прогноза по модели

Далее появится диалоговое окно выбора параметров для прогнозирования (рисунок 2.52).

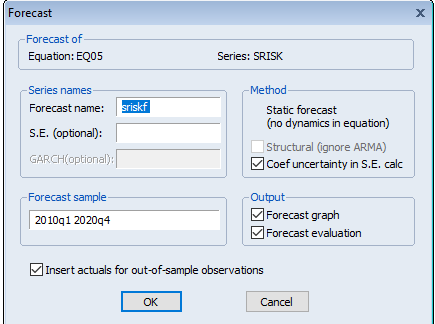
Рисунок 2.52. Диалоговое окно для построения прогноза по модели

Eviews позволяет построить прогноз как по исходной панельной переменной, так и по предварительно преобразованной. Кроме того Eviews имеет возможность построения статических прогнозов, не предполагающих самокорректирующихся на каждом шаге прогноза по ретроспективным данным, и возможность построения динамических прогнозов. Для выбора методов построения прогнозов следует в рамке Method установить переключатель на Dynamicforecast или  Staticforecast. В поле Forecastsample следует указать период упреждения прогноза в виде даты начала его и конца через пробел.

На рисунке 2.53 представлен график, отражающий построенный прогноз по модели, справа от графика перечислены значения всех показателей качества прогноза по панельной модели:

- RootMeanSquaredError (квадратный корень средней ошибки предсказания);

- MeanAbsoluteError(средняя ошибка по модулю);

- MeanAbsolutePercentageError(средняяошибкааппроксимации);

- TheilInequalityCoefficient (коэффициентнеравенстваТейла);

- BiasProportion(доля систематической ошибки);

- Variance Proportion (долявариации);

- CovarianceProportion(доляковариации).

Здесь на графике (рисунок 2.53) синим цветом выделены прогнозные значения показателя, полученные по панельной модели, а красным указаны границы доверительного интервала, определенные шириной двух стандартных отклонений.

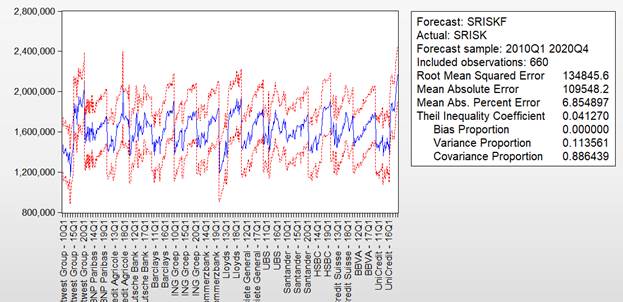
Рисунок 2.53. Прогноз по панельной модели