Транспортная задача - пример решения.
Ниже приведено условие задачи и текстовая часть решения. Закачка полного решения, файлы doc, mcd и xls в архиве zip, начнется автоматически через 10 секунд.
Имеются n пунктов производства и m пунктов распределения продукции. Стоимость перевозки единицы продукции с i-го пункта производства в j-й центр распределения cij приведена в таблице, где под строкой понимается пункт производства, а под столбцом – пункт распределения. Кроме того, в этой таблице в i-й строке указан объем производства в i-м пункте производства, а в j-м столбце указан спрос в j-м центре распределения. Необходимо составить план перевозок по доставке требуемой продукции в пункты распределения, минимизирующий суммарные транспортные расходы.
|
Стоимость перевозки единицы продукции |
Объем производства |
||||
|
|
j1 |
j2 |
j3 |
j4 |
|
|
i1 |
8 |
9 |
6 |
8 |
21 |
|
i2 |
7 |
8 |
4 |
9 |
22 |
|
i3 |
8 |
7 |
2 |
4 |
23 |
|
i4 |
7 |
5 |
12 |
6 |
24 |
|
Объем потребления |
20 |
30 |
18 |
24 |
|
Решение в Mathcad.
Специальной командой ORIGIN присваиваем значение 1 первому элементу столбца и строки, вводимых матриц.
![]()
Вводим исходные данные задачи в матричной форме.

Затем находим суммы элементов матриц a и b, и устанавливаем, какую модель имеет задача – открытую или закрытую.
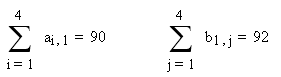
Суммы не равны, следовательно, задача имеет открытую модель.
Вводим линейную целевую функцию.
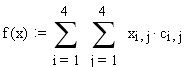
Вводим ограничения в матричной форме.
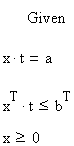
Определяем с помощью функции Minimize оптимальное решение задачи.

План перевозок представлен матрицей х. При данном плане перевозок затраты будут минимальными и составят 484 ден. ед.
Решение в EXCEL.
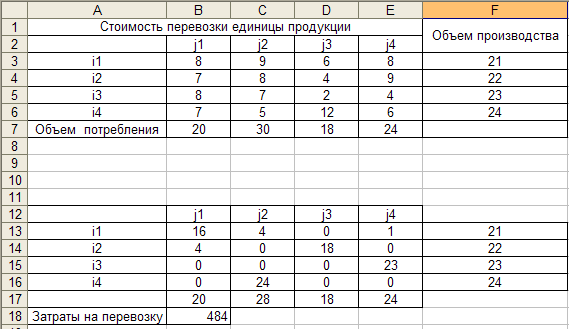
Составляем таблицу исходных данных
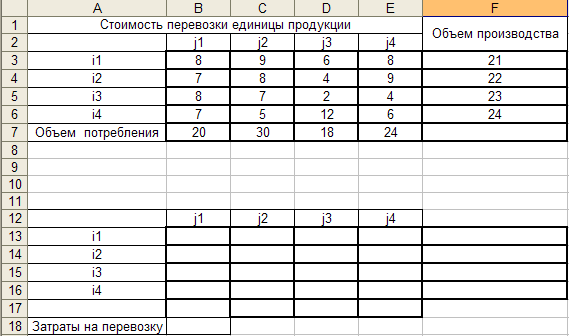
Далее вводим формулы в ячейки:
В ячейку F13 формулу =СУММ(B13:E13). Объёмы перевозимой продукции от пункта производства i1.
В ячейку F14 формулу =СУММ(B14:E14). Объёмы перевозимой продукции от пункта производства i2.
В ячейку F15 формулу =СУММ(B15:E15). Объёмы перевозимой продукции от пункта производства i3.
В ячейку F16 формулу =СУММ(B16:E16). Объёмы перевозимой продукции от пункта производства i4.
В ячейку F17 формулу =СУММ(B13:E16). Объёмы перевозимой продукции к пункту распределения j1.
В ячейку C17 формулу =СУММ(C13:C16). Объёмы перевозимой продукции к пункту распределения j2.
В ячейку D17 формулу =СУММ(D13:D16). Объёмы перевозимой продукции к пункту распределения j3.
В ячейку E17 формулу =СУММ(E13:E16). Объёмы перевозимой продукции к пункту распределения j4.
В ячейку B18 формулу =СУММПРОИЗВ(B3:E6;B13:E16). Затраты на перевозимую продукцию от пункта производства к пункту распределения. Именно эта величина должна быть минимальной при перевозки продукции. Сами искомые объекты перевозок находятся в ячейках B13:E16. Начальные значения объёмов перевозок вводим равные нулю. При выполнении поиска решения в этих ячейках будут оптимальные значения объёмов перевозок. После ввода формул и начальных значений таблица примет вид:
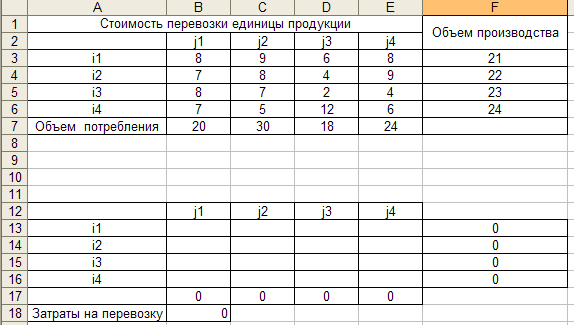
В ячейке B18 находится формула вычисления затрат на перевозку продукции. Затраты на перевозку должны быть минимальными. Эта ячейка в терминологии Excel будет являться целевой. Для осуществления поиска решения необходимо задать ограничения и условия поиска. Выполняем действия Сервис/Поиск решения. На экране появляется диалоговое окно Поиска решения.
В этой форме устанавливаем целевую ячейку $B$18 минимальному значению. Изменяя ячейки $B$13:$E$16. Для того, чтобы ввести адреса ячеек, нужно щелкнуть на значке справа от поля ввода, и затем в таблице выделить область (группу ячеек). Для того, чтобы задать ограничения, необходимо щелкнуть на кнопке Добавить. После этого появится форма для ввода ограничений.
Вводим ограничения:
$B$13:$E$16 >= 0
И т. д.
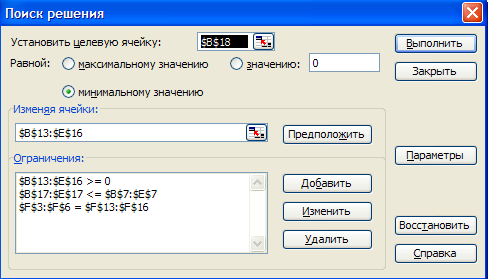
Так как мы осуществляем поиск минимального значения, то можем получить отрицательные значения. Что является нежелательным в нашей задаче. Поэтому необходимо щелкнуть на кнопке Параметры и отметить пункт неотрицательные значения и щелкнуть ОК.
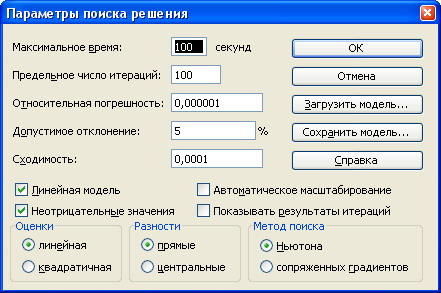
Затем щелкнуть на кнопке Выполнить. После этого на экране появятся результаты поиска. Щелкнуть на кнопку ОК.
В ячейках B13:E16 находятся значения, определяющие оптимальный план перевозок продукции. В нашей задаче затраты на перевозку составляют 484 условных денежных единиц.
Имя файла: 10.rar
Размер файла: 196.39 Kb
Если закачивание файла не начнется через 10 сек, кликните по этой ссылке
